Σελίδα 1 από 3
Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 9:05 am
από Επιτροπή Θεμάτων 2023
Αγαπητές/τοί φίλες/οι
Στο θέμα αυτό θα αναρτηθούν (αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου) και, αποκλειστικά, θα λυθούν τα θέματα των
Μαθηματικών προσανατολισμού 2018 των Ημερησίων ΓΕΛ. Επομένως σχολιασμοί-κριτική επί της δυσκολίας κ.λ.π. των θεμάτων θα απομακρύνονται από αυτήν την συζήτηση. Μπορούν να γίνουν στο
Σχόλια στα Μαθηματικά προσανατολισμού 2018
edit: Προστέθηκαν τα θέματα.
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 10:24 am
από xr.tsif
ανεβάζω τα θέματα σε .docx
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 11:15 am
από Πρωτοπαπάς Λευτέρης
Δ1. Η συνάρτηση

με

και

είναι ορισμένη και συνεχής στο

ως διαφορά των συνεχών συναρτήσεων με τύπους

(συνεχής ως σύνθεση των συνεχών

-γινόμενο εκθετικής με σταθερά- και της

-πολυωνυμική) και

(συνεχής ως πολυωνυμική).
Επίσης η συνάρτηση

είναι παραγωγίσιμη στο

ως διαφορά των παραγωγίσιμων συναρτήσεων με τύπους

(παραγωγίσιμη ως σύνθεση των παραγωγίσιμων

-γινόμενο εκθετικής με σταθερά- και της

-πολυωνυμική) και

(παραγωγίσιμη ως πολυωνυμική) με

.
Επίσης η συνάρτηση

είναι δύο φορές παραγωγίσιμη στο

ως διαφορά των παραγωγίσιμων συναρτήσεων με τύπους

(παραγωγίσιμη ως σύνθεση των παραγωγίσιμων

-γινόμενο εκθετικής με σταθερά- και της

-πολυωνυμική) και

(παραγωγίσιμη ως πολυωνυμική) με

.
Τότε:

,

και

,
δηλαδή η

παρουσιάζει μοναδικό σημείο καμπής το

δηλαδή το

.
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 11:23 am
από Γιώργος Ρίζος
Γ1. Έστω

η πλευρά του τετραγώνου, άρα

η περίμετρός του, οπότε

η περίμετρος

του κύκλου ακτίνας

με

.
Τότε

, οπότε

.
Γ2. Η συνάρτηση

που δίνει το ολικό εμβαδό είναι παραγωγίσιμη στο Π.Ο. της με

Από πίνακα μονοτονίας-ακροτάτων βρίσκουμε ότι έχει ολικό ελάχιστο για

.
Τότε η πλευρά του τετραγώνου είναι

και η διάμετρος του κύκλου είναι

Γ3. Παίρνουμε τη γενίκευση της συνάρτησης

στο
![[0,8] [0,8]](/forum/ext/geomar/texintegr/latexrender/pictures/61464d90bc2ae67b93035582c6e220af.png)
.
Είναι
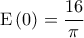
και

.
Είναι

.
Οπότε, αφού η

είναι συνεχής, γν. φθίνουσα στο
![\displaystyle \left[ {0,\;\frac{{32}}{{\pi + 4}}} \right] \displaystyle \left[ {0,\;\frac{{32}}{{\pi + 4}}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/3f3557fc2663589a9bd594f2d52d8a5e.png)
και γν. αύξουσα στο
![\displaystyle \left[ {\frac{{32}}{{\pi + 4}},\;8} \right] \displaystyle \left[ {\frac{{32}}{{\pi + 4}},\;8} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fbb53769f2d3ea993045931c4c93aa39.png)
υπάρχει ένα μοναδικό

στο

τέτοιο ώστε

.
edit: Διόρθωσα ένα τυπογραφικό λάθος.
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 11:31 am
από gbaloglou
Για το Δ4: ευθεία λύση (χωρίς χρήση των προηγηθέντων μερών) από την γνωστή (ή έστω εύκολα αποδεικνυόμενη) ανισότητα

, αφού προηγηθεί ακριβής υπολογισμός του ολοκληρώματος

: αρκεί να χρησιμοποιηθεί η προφανής αντικατάσταση

στο ολοκλήρωμα

. (Η ίδια αντικατάσταση και για το πρώτο ολοκλήρωμα.)
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 11:33 am
από mick7
Έχουν αναρτηθεί οι λύσεις από τον κ. Ξένο...Καλή επιτυχία σε όλους τους διαγωνιζόμενους...
http://omathimatikos.gr/%CE%B4%CE%B5%CE ... %BF%CF%83/
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 11:35 am
από gavrilos
Καλημέρα και καλή επιτυχία στους υποψήφιους.
Η (μάλλον "λογική") απάντηση στο (δύσκολο) Δ4.
Η

είναι κυρτή στο διάστημα

άρα βρίσκεται πάνω από την εφαπτομένη της

στο

.Η ευθεία αυτή έχει εξίσωση

.
Συνεπώς

.
Edit: Μία ακόμη λύση,με όχι σχολικά εργαλεία,θα μπορούσε να προκύψει με αλλαγή μεταβλητής

και χρήση της

.
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 11:37 am
από pavlospallas
Το θέμα Γ στην πιο γενική του μορφή είναι η άσκηση 6 στη σελίδα 46 του βιβλίου της Γενικής.
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 11:44 am
από Πρωτοπαπάς Λευτέρης
Δ2. Έχουμε ότι:
*

,
*

, αφού

και

και
*
![\displaystyle{\lim_{x \rightarrow +\infty}f'(x)=\lim_{x \rightarrow -\infty}(2e^{x-a}-2x)=\lim_{x \righatrrow -\infty}\left[2e^{x-a}\left(1-\frac{x}{e^{x-a}\right)\right]=+\infty} \displaystyle{\lim_{x \rightarrow +\infty}f'(x)=\lim_{x \rightarrow -\infty}(2e^{x-a}-2x)=\lim_{x \righatrrow -\infty}\left[2e^{x-a}\left(1-\frac{x}{e^{x-a}\right)\right]=+\infty}](/forum/ext/geomar/texintegr/latexrender/pictures/5f7abdaaa0ce3470af5a6e6d7304c6cc.png)
, αφού

,

(αφού τηρούνται οι προυποθέσεις του θεωρήματος De L' Hospital).
Από το Δ1 αποδείξαμε ότι η συνάρτηση

είναι κοίλη στο
![(-\infty,a] (-\infty,a]](/forum/ext/geomar/texintegr/latexrender/pictures/b1868caa9fa0259f8d2269e6c126e219.png)
και κυρτή στο

,
οπότε η

είναι γνησίως φθίνουσα στο
![(-\infty,a] (-\infty,a]](/forum/ext/geomar/texintegr/latexrender/pictures/b1868caa9fa0259f8d2269e6c126e219.png)
και γνησίως αύξουσα στο

.
Η

είναι συνεχής (ως παραγωγίσιμη) και γνησίως φθίνουσα στο
![A_1=(-\infty,a] A_1=(-\infty,a]](/forum/ext/geomar/texintegr/latexrender/pictures/3a0caecf2f9cae724adebfe091d48086.png)
, οπότε

.
Επίσης

είναι συνεχής (ως παραγωγίσιμη) και γνησίως αύξουσα στο

, οπότε

.
Αφού

,
οπότε

και γνησίως μονότονη σε κάθε ένα από τα

,
οπότε η

έχει από μία ακριβώς ρίζα σε κάθε ένα από τα διαστήματα

, έστω

.
Συνεπώς:
**

, άρα η

είναι γνησίως αύξουσα στο
![(-\infty,x_1] (-\infty,x_1]](/forum/ext/geomar/texintegr/latexrender/pictures/1bf043fc45ba6b853d610dd09d819740.png)
,
**

, άρα η

είναι γνησίως φθίνουσα στο
![[x_1,a] [x_1,a]](/forum/ext/geomar/texintegr/latexrender/pictures/b146a7bed29eb56990bb8ee9d256aa53.png)
,
**

, άρα η

είναι γνησίως φθίνουσα στο
![[a,x_2] [a,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/53e93863bfb8608a17600eae6b5d9681.png)
,
**

, άρα η

είναι γνησίως αύξουσα στο
![[x_2,+\infty)] [x_2,+\infty)]](/forum/ext/geomar/texintegr/latexrender/pictures/61b29eb1fe0ce09c235a131f470f3796.png)
.
Επιπλέον η συνάρτηση

είναι συνεχής στο

, οπότε είναι γνησίως φθίνουσα στο
![[x_1,x_2] [x_1,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/e2928e128099d8ebc393e5079c62ab4c.png)
.
Συνεπώς η συνάρτηση

παρουσιάζει μοναδικό τοπικό μέγιστο για
![x_1 \in (-\infty,a] x_1 \in (-\infty,a]](/forum/ext/geomar/texintegr/latexrender/pictures/86d4ac4de2707851384fa07ad963c841.png)
και μοναδικό τοπικό ελάχιστο για

.
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 11:50 am
από efakop
Στο Δ3 πρέπει να αποδείξεις ότι

για να πεις ότι η εξίσωση δεν έχει λύση. Και αποδεικνύεται αφού

και

γν. φθίνουσα στο

με

ρίζα της παραγώγου.
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 11:55 am
από kkoudas
Το Δ3 του κ. Ξένου είναι λάθος. Εφάρμοσε την μονοτονία του
![[\alpha,x_2] [\alpha,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/c7115dfb8f46549c10399f8633124b63.png)
, για να γνωματεύσει περί ανισότητας για το

. Πρέπει να δειχθεί ότι

.
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 12:08 pm
από killbill
Γιώργος Ρίζος έγραψε: ↑Δευ Ιουν 11, 2018 11:23 am
Γ1. Έστω

η πλευρά του τετραγώνου, οπότε

η περίμετρος

του κύκλου ακτίνας

με

.
Τότε

, οπότε

.
Γ2. Η συνάρτηση

που δίνει το ολικό εμβαδό είναι παραγωγίσιμη στο Π.Ο. της με

Είναι -64χ και όχι -64π, οπότε είναι λάθος και όλος ο υπόλοιπος συλλογισμός
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 12:19 pm
από diomides
θεμα Γ υπαρχει στα μαθηματικα γενικης παιδειας σελ.45
παλιοτερα το καναμε παντα, κλασσικο θεμα
τα δυο πρωτα ερωτηματα
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 12:25 pm
από evry
Η πλευρά του τετραγώνου δεν είναι

, αφού το

είναι η περίμετρος του τετραγώνου;
Γιώργος Ρίζος έγραψε: ↑Δευ Ιουν 11, 2018 11:23 am
Γ1. Έστω

η πλευρά του τετραγώνου, οπότε

η περίμετρος

του κύκλου ακτίνας

με

.
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 12:36 pm
από ΛΕΥΤΕΡΗΣ
Η συνάρτηση του Δ θεματος υπάρχει ακριβώς ίδια στο σχολικό βιβλιο σελ 278 ασκ2 β ομαδας
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 12:37 pm
από achilleas
Δ1. Παρατηρούμε ότι η συνάρτηση

είναι δύο φορές παραγωγίσιμη με

και

Η 2η παράγωγος της

υπάρχει για κάθε

, οπότε αναζητούμε τις τετμημένες των σημείων καμπής στις λύσεις τις

.
Είναι

Λόγω της μονοτονίας της εκθετικής συνάρτησης είναι

για

, και

για

.
Συνεπώς, η

αλλάζει πρόσημο εκατέρωθεν του

.
Έτσι, η συνάρτηση

έχει μοναδικό σημείο καμπής το

Δ2. Θεωρούμε τη συνάρτηση

με

για

και παρατηρούμε ότι
η

αλλάζει πρόσημο εκατέρωθεν του

.
Μάλιστα, η

είναι γνησίως φθίνουσα για

και γνησίως αύξουσα για

Επιπλέον, είναι

,

,

και

, όπου
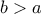
είναι τέτοιο ώστε

(η ύπαρξη του

έπεται από το ότι

)
Από Bolzano υπάρχουν

και

τέτοια ώστε

Από την μονοτονία της

στα διαστήματα

και

έπεται η μοναδικότητα των

και το ότι η

έχει τοπικό μέγιστο στο

και τοπικό ελάχιστο στο

, αφού η

θα διατηρεί σταθερό πρόσημο σε καθένα από τα διαστήματα

(θετικό),

(αρνητικό) και

(θετικό).
![\displaystyle
\begin{array}{|c|ccccccccccccccc|}
\hline
x&-\infty & &&x_1&&&&&x_2&&&&&&+\infty\\[0.2cm]
\hline
g(x)&& + & &0&&-&&&0&&&&+&& \\ [0.2cm]
\hline
f&& \nearrow &&\text{T. M. }&&\searrow&&&\text{T. E. }&&&&\nearrow&& \\ [0.2cm]
\hline
\end{array}
\displaystyle
\begin{array}{|c|ccccccccccccccc|}
\hline
x&-\infty & &&x_1&&&&&x_2&&&&&&+\infty\\[0.2cm]
\hline
g(x)&& + & &0&&-&&&0&&&&+&& \\ [0.2cm]
\hline
f&& \nearrow &&\text{T. M. }&&\searrow&&&\text{T. E. }&&&&\nearrow&& \\ [0.2cm]
\hline
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/15ef46826d32c2abaa3dda5d62635ee3.png)
Δ3. Έστω ότι υπήρχε

τέτοιο ώστε

Από ΘΜΤ θα υπήρχε

τέτοιο ώστε

, δηλ.

. Αφού

, αναγκαστικά θα είναι

, άτοπο, αφού

Δ4. Η εφαπτομένη της

στο

έχει εξίσωση

Αφού

η εξίσωση γράφεται

Λόγω της κυρτότητας της

στο
![[2,3] [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png)
είναι

για κάθε
![x\in (2,3] x\in (2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/7743659bcf2aaea50d183ac3940c4799.png)
και άρα

,
όπως θέλαμε.
****************************
Επεξεργασία 2:54μμ:
Αλλιώς για την ύπαρξη του 
: Η συνάρτηση

με

έχει

κι άρα είναι αύξουσα στο

με

για

.
Έτσι, είναι

για κάθε

, οπότε

για

****************************
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 12:52 pm
από killbill
Γιώργος Ρίζος έγραψε: ↑Δευ Ιουν 11, 2018 11:23 am
Γ3. Παίρνουμε τη γενίκευση της συνάρτησης

στο
![[0,8] [0,8]](/forum/ext/geomar/texintegr/latexrender/pictures/61464d90bc2ae67b93035582c6e220af.png)
.
Είναι

και

.
Είναι

.
Οπότε, αφού η

είναι συνεχής, γν. φθίνουσα στο
![\displaystyle \left[ {0,\;\frac{{32}}{{\pi + 4}}} \right] \displaystyle \left[ {0,\;\frac{{32}}{{\pi + 4}}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/3f3557fc2663589a9bd594f2d52d8a5e.png)
και γν. αύξουσα στο
![\displaystyle \left[ {\frac{{32}}{{\pi + 4}},\;8} \right] \displaystyle \left[ {\frac{{32}}{{\pi + 4}},\;8} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fbb53769f2d3ea993045931c4c93aa39.png)
υπάρχει ένα μοναδικό

στο

τέτοιο ώστε

.
edit: Διόρθωσα ένα τυπογραφικό λάθος.
Το τυπογραφικό λάθος που ορθώς διόρθωσες, συνεπάγεται και διόρθωση των τιμών

και

στη συνέχεια
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 12:57 pm
από killbill
ΛΕΥΤΕΡΗΣ έγραψε: ↑Δευ Ιουν 11, 2018 12:36 pm
Η συνάρτηση του Δ θεματος υπάρχει ακριβώς ίδια στο σχολικό βιβλιο σελ 278 ασκ2 β ομαδας
σελίδα 160 στην τρέχουσα έκδοση
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 1:37 pm
από margk
Διεγραψα την απαντηση στο Δ3 διοτι ηταν λανθασμενη.
Re: Μαθηματικά προσανατολισμού 2018 (Θέματα & Λύσεις)
Δημοσιεύτηκε: Δευ Ιουν 11, 2018 1:44 pm
από stranton
Το Γ3 απ' ευθείας
Θα αποδείξουμε ότι η εξίσωση

έχει μοναδική λύση στο διάστημα

.
Είναι


.
Είναι

.
Οι λύσεις της εξίσωσης είναι:

Όμως η

αφού

Ακόμα

αφού

και

αφού

Πράγματι, το τριώνυμο
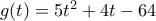
είναι αρνητικό όταν

και το

ανήκει σ' αυτό το διάστημα.
 με
με  και
και  είναι ορισμένη και συνεχής στο
είναι ορισμένη και συνεχής στο  ως διαφορά των συνεχών συναρτήσεων με τύπους
ως διαφορά των συνεχών συναρτήσεων με τύπους  (συνεχής ως σύνθεση των συνεχών
(συνεχής ως σύνθεση των συνεχών  -γινόμενο εκθετικής με σταθερά- και της
-γινόμενο εκθετικής με σταθερά- και της  -πολυωνυμική) και
-πολυωνυμική) και  (συνεχής ως πολυωνυμική).
(συνεχής ως πολυωνυμική). .
. (παραγωγίσιμη ως πολυωνυμική) με
(παραγωγίσιμη ως πολυωνυμική) με  .
. ,
,
 ,
, παρουσιάζει μοναδικό σημείο καμπής το
παρουσιάζει μοναδικό σημείο καμπής το  δηλαδή το
δηλαδή το  .
. η πλευρά του τετραγώνου, άρα
η πλευρά του τετραγώνου, άρα  η περίμετρός του, οπότε
η περίμετρός του, οπότε  η περίμετρος
η περίμετρος  του κύκλου ακτίνας
του κύκλου ακτίνας  με
με  .
. , οπότε
, οπότε  .
. που δίνει το ολικό εμβαδό είναι παραγωγίσιμη στο Π.Ο. της με
που δίνει το ολικό εμβαδό είναι παραγωγίσιμη στο Π.Ο. της με 
 .
. και η διάμετρος του κύκλου είναι
και η διάμετρος του κύκλου είναι 
 στο
στο ![[0,8] [0,8]](/forum/ext/geomar/texintegr/latexrender/pictures/61464d90bc2ae67b93035582c6e220af.png) .
. 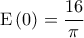 και
και  .
. .
.![\displaystyle \left[ {0,\;\frac{{32}}{{\pi + 4}}} \right] \displaystyle \left[ {0,\;\frac{{32}}{{\pi + 4}}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/3f3557fc2663589a9bd594f2d52d8a5e.png) και γν. αύξουσα στο
και γν. αύξουσα στο ![\displaystyle \left[ {\frac{{32}}{{\pi + 4}},\;8} \right] \displaystyle \left[ {\frac{{32}}{{\pi + 4}},\;8} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fbb53769f2d3ea993045931c4c93aa39.png) υπάρχει ένα μοναδικό
υπάρχει ένα μοναδικό  στο
στο  τέτοιο ώστε
τέτοιο ώστε  .
. , αφού προηγηθεί ακριβής υπολογισμός του ολοκληρώματος
, αφού προηγηθεί ακριβής υπολογισμός του ολοκληρώματος  : αρκεί να χρησιμοποιηθεί η προφανής αντικατάσταση
: αρκεί να χρησιμοποιηθεί η προφανής αντικατάσταση  στο ολοκλήρωμα
στο ολοκλήρωμα  . (Η ίδια αντικατάσταση και για το πρώτο ολοκλήρωμα.)
. (Η ίδια αντικατάσταση και για το πρώτο ολοκλήρωμα.) άρα βρίσκεται πάνω από την εφαπτομένη της
άρα βρίσκεται πάνω από την εφαπτομένη της  .Η ευθεία αυτή έχει εξίσωση
.Η ευθεία αυτή έχει εξίσωση  .
. .
. και χρήση της
και χρήση της  .
. ,
, , αφού
, αφού  και
και  και
και![\displaystyle{\lim_{x \rightarrow +\infty}f'(x)=\lim_{x \rightarrow -\infty}(2e^{x-a}-2x)=\lim_{x \righatrrow -\infty}\left[2e^{x-a}\left(1-\frac{x}{e^{x-a}\right)\right]=+\infty} \displaystyle{\lim_{x \rightarrow +\infty}f'(x)=\lim_{x \rightarrow -\infty}(2e^{x-a}-2x)=\lim_{x \righatrrow -\infty}\left[2e^{x-a}\left(1-\frac{x}{e^{x-a}\right)\right]=+\infty}](/forum/ext/geomar/texintegr/latexrender/pictures/5f7abdaaa0ce3470af5a6e6d7304c6cc.png) , αφού
, αφού ,
, (αφού τηρούνται οι προυποθέσεις του θεωρήματος De L' Hospital).
(αφού τηρούνται οι προυποθέσεις του θεωρήματος De L' Hospital).![(-\infty,a] (-\infty,a]](/forum/ext/geomar/texintegr/latexrender/pictures/b1868caa9fa0259f8d2269e6c126e219.png) και κυρτή στο
και κυρτή στο  ,
, είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![A_1=(-\infty,a] A_1=(-\infty,a]](/forum/ext/geomar/texintegr/latexrender/pictures/3a0caecf2f9cae724adebfe091d48086.png) , οπότε
, οπότε  .
. , οπότε
, οπότε  .
. ,
, και γνησίως μονότονη σε κάθε ένα από τα
και γνησίως μονότονη σε κάθε ένα από τα  ,
, έχει από μία ακριβώς ρίζα σε κάθε ένα από τα διαστήματα
έχει από μία ακριβώς ρίζα σε κάθε ένα από τα διαστήματα  .
. , άρα η
, άρα η ![(-\infty,x_1] (-\infty,x_1]](/forum/ext/geomar/texintegr/latexrender/pictures/1bf043fc45ba6b853d610dd09d819740.png) ,
, , άρα η
, άρα η ![[x_1,a] [x_1,a]](/forum/ext/geomar/texintegr/latexrender/pictures/b146a7bed29eb56990bb8ee9d256aa53.png) ,
, , άρα η
, άρα η ![[a,x_2] [a,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/53e93863bfb8608a17600eae6b5d9681.png) ,
, , άρα η
, άρα η ![[x_2,+\infty)] [x_2,+\infty)]](/forum/ext/geomar/texintegr/latexrender/pictures/61b29eb1fe0ce09c235a131f470f3796.png) .
. , οπότε είναι γνησίως φθίνουσα στο
, οπότε είναι γνησίως φθίνουσα στο ![[x_1,x_2] [x_1,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/e2928e128099d8ebc393e5079c62ab4c.png) .
.![x_1 \in (-\infty,a] x_1 \in (-\infty,a]](/forum/ext/geomar/texintegr/latexrender/pictures/86d4ac4de2707851384fa07ad963c841.png) και μοναδικό τοπικό ελάχιστο για
και μοναδικό τοπικό ελάχιστο για  .
. για να πεις ότι η εξίσωση δεν έχει λύση. Και αποδεικνύεται αφού
για να πεις ότι η εξίσωση δεν έχει λύση. Και αποδεικνύεται αφού  και
και  με
με  ρίζα της παραγώγου.
ρίζα της παραγώγου.![[\alpha,x_2] [\alpha,x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/c7115dfb8f46549c10399f8633124b63.png) , για να γνωματεύσει περί ανισότητας για το
, για να γνωματεύσει περί ανισότητας για το  . Πρέπει να δειχθεί ότι
. Πρέπει να δειχθεί ότι  .
. .
. που δίνει το ολικό εμβαδό είναι παραγωγίσιμη στο Π.Ο. της με
που δίνει το ολικό εμβαδό είναι παραγωγίσιμη στο Π.Ο. της με 
 , οπότε αναζητούμε τις τετμημένες των σημείων καμπής στις λύσεις τις
, οπότε αναζητούμε τις τετμημένες των σημείων καμπής στις λύσεις τις .
.
 για
για  , και
, και  για
για  .
. αλλάζει πρόσημο εκατέρωθεν του
αλλάζει πρόσημο εκατέρωθεν του  .
.
 με
με  για
για  αλλάζει πρόσημο εκατέρωθεν του
αλλάζει πρόσημο εκατέρωθεν του  Επιπλέον, είναι
Επιπλέον, είναι ,
,  ,
,  και
και  , όπου
, όπου 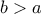 είναι τέτοιο ώστε
είναι τέτοιο ώστε 
 έπεται από το ότι
έπεται από το ότι  )
) και
και  τέτοια ώστε
τέτοια ώστε 
 και
και  έπεται η μοναδικότητα των
έπεται η μοναδικότητα των  και το ότι η
και το ότι η  , αφού η
, αφού η  (θετικό),
(θετικό),  (αρνητικό) και
(αρνητικό) και  (θετικό).
(θετικό).![\displaystyle
\begin{array}{|c|ccccccccccccccc|}
\hline
x&-\infty & &&x_1&&&&&x_2&&&&&&+\infty\\[0.2cm]
\hline
g(x)&& + & &0&&-&&&0&&&&+&& \\ [0.2cm]
\hline
f&& \nearrow &&\text{T. M. }&&\searrow&&&\text{T. E. }&&&&\nearrow&& \\ [0.2cm]
\hline
\end{array}
\displaystyle
\begin{array}{|c|ccccccccccccccc|}
\hline
x&-\infty & &&x_1&&&&&x_2&&&&&&+\infty\\[0.2cm]
\hline
g(x)&& + & &0&&-&&&0&&&&+&& \\ [0.2cm]
\hline
f&& \nearrow &&\text{T. M. }&&\searrow&&&\text{T. E. }&&&&\nearrow&& \\ [0.2cm]
\hline
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/15ef46826d32c2abaa3dda5d62635ee3.png)
 τέτοιο ώστε
τέτοιο ώστε  Από ΘΜΤ θα υπήρχε
Από ΘΜΤ θα υπήρχε  τέτοιο ώστε
τέτοιο ώστε  , δηλ.
, δηλ.  . Αφού
. Αφού  , αναγκαστικά θα είναι
, αναγκαστικά θα είναι  , άτοπο, αφού
, άτοπο, αφού 
 έχει εξίσωση
έχει εξίσωση 
 η εξίσωση γράφεται
η εξίσωση γράφεται 
![[2,3] [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png) είναι
είναι  για κάθε
για κάθε ![x\in (2,3] x\in (2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/7743659bcf2aaea50d183ac3940c4799.png) και άρα
και άρα ,
, με
με  έχει
έχει  κι άρα είναι αύξουσα στο
κι άρα είναι αύξουσα στο  για
για  .
. για κάθε
για κάθε 

 και
και  .
. και
και  στη συνέχεια
στη συνέχεια έχει μοναδική λύση στο διάστημα
έχει μοναδική λύση στο διάστημα  .
.
 .
.  .
. 
 αφού
αφού 
 αφού
αφού 
 αφού
αφού 
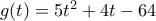 είναι αρνητικό όταν
είναι αρνητικό όταν  και το
και το  ανήκει σ' αυτό το διάστημα.
ανήκει σ' αυτό το διάστημα.