Μαθηματικά προσαν. (κατεύθ.) 2016

#121

GiorgosSim έγραψε:
cretanman έγραψε:Εναλλακτικός τρόπος για το Γ4

Θα δείξουμε ότι η είναι μοναδική λύση της εξίσωσης.

Υποθέτουμε λοιπόν, αντίθετα, ότι υπάρxει που να είναι λύση της εξίσωσης. Ισxύει $|\eta\mu x_0|<x_0$ (από τη γνωστή ανισότητα $|\eta\mu x|\leq |x|$ με ισότητα μόνο για ) καθώς επίσης $|\eta\mu x_0|< |\eta\mu x_0|+3$ και .

Διακρίνουμε τις περιπτώσεις:

$\bullet$ Αν $|\eta\mu x_0|+3<x_0$ τότε $|\eta\mu x_0|< |\eta\mu x_0|+3<x_0<x_0+3$ και επειδή ισxύουν οι προϋποθέσεις του ΘΜΤ σε κάθε ένα από τα διαστήματα $\left[|\eta\mu x_0|, |\eta\mu x_0|+3\right], \ \left[x_0,x_0+3\right]$ άρα υπάρxουν $\xi_1 \in \left(|\eta\mu x_0|, |\eta\mu x_0|+3\right) , \ \xi_2 \in \left(x_0,x_0+3\right)$ ώστε η εξίσωση να γράφεται:

$3f'(\xi_1)=3f'(\xi_2)$ απ΄όπου $f'(\xi_1)=f'(\xi_2)$ και αφού η είναι γνησίως αύξουσα (ως κυρτή) άρα είναι και κι έτσι παίρνουμε $\xi_1=\xi_2$ , πράγμα άτοπο αφού τα $\xi_1, \xi_2$ ανήκουν σε διαφορετικά διαστήματα.

$\bullet$ Αν $x_0\leq |\eta\mu x_0|+3$ τότε $|\eta\mu x_0|<x_0\leq |\eta\mu x_0|+3<x_0+3$ .

Γράφουμε την εξίσωση στη μορφή: $f(x_0)-f\left(|\eta\mu x_0|\right)=f(x_0+3)-f\left(|\eta\mu x_0|+3\right)$

Επειδή ισxύουν οι προϋποθέσεις του ΘΜΤ σε κάθε ένα από τα διαστήματα $\left[|\eta\mu x_0|, x_0\right], \ \left[|\eta\mu x_0|+3, x_0+3\right]$ άρα υπάρxουν $\xi_1 \in \left(|\eta\mu x_0|, x_0) , \ \xi_2 \in \left(|\eta\mu x_0|+3, x_0+3\right)$ ώστε η εξίσωση να γράφεται:

$(x_0-|\eta\mu x_0|)f'(\xi_1)=(x_0-|\eta\mu x_0|)f'(\xi_2)$ και αφού $x_0-|\eta\mu x_0|\neq 0$ άρα $f'(\xi_1)=f'(\xi_2)$ και αφού η είναι γνησίως αύξουσα (ως κυρτή) άρα είναι και , κι έτσι παίρνουμε $\xi_1=\xi_2$ , πράγμα άτοπο αφού τα $\xi_1, \xi_2$ ανήκουν σε διαφορετικά διαστήματα.

Χαιρετώ την αγαπητή παρέα του . Ολόιδια ακριβώς λύση με τον κ. Cretaman έκανα. Απλά έχω ενδοιασμούς μήπως υπάρχει κάποιο πρόβλημα στα διαστήματα και μπλέκονται σε κάποια περίπτωση.

Δεν τίθεται τέτοιο θέμα. Αυτός είναι και ο λόγος που παίρνουμε περιπτώσεις (στη δεύτερη περίπτωση τροποποιούμε και την εξίσωση): Για να μην έχουμε αλληλοεπικάλυψη διαστημάτων και έτσι να καταλήξουμε σε άτοπο.

daphne.man · #122

Καλησπέρα και από μένα.

Συμφωνώ με την παρατήρηση του Χρήστου, και γι' αυτό απαντώ παραθέτοντάς την ξανά:
«Δεν είναι δυνατόν η μαθηματική μας κουλτούρα να περιορίζεται στην Ανάλυση, και σε εξετάσεις εισαγωγής να προσπαθούμε να βάλουμε «τεχνικά» θέματα, ανούσιες λεπτομέρειες και παγίδες...» Ας διευρυνθεί η ύλη των Μαθηματικών, να υπάρχει επέκτασή της και σε άλλους τομείς και ας μην επικεντρωνόμαστε σε ένα τομέα των μαθηματικών, εισάγοντας διάφορες τεχνικές δυσκολίες στην εξέταση (που γίνεται για να ξεχωρίσουν οι "καλοί" από τους "άριστους". Εξ'αλλου, σε ποιόν θα χρησιμεύσει η δυνατότητα διαχείρισης της "παγίδας" στα μαθηματικά; Γιατί είναι πιο σημαντικό το να ξέρει ο νέος να διαχειρίζεται "παγίδες" στην ανάλυση από το να ξέρει γεωμετρία ή άλγεβρα;

Δάφνη Μανουσάκη

Y.Γ. Διδάσκω μαθηματικά (Λογισμό 1) στο Α εξάμηνο πανεπιστημιακής σχολής. Παρ' όλο που μεγάλο μέρος της ύλης του μαθήματος έχει ήδη καλυφθεί στα μαθηματικά κατεύθυνσης της Γ λυκείου, οι φοιτητές δε φαίνεται να έχουν κατανοήσει τις έννοιες που καλούνται να διαχειριστούν. Αναρωτιέμαι λοιπόν, εάν σε αυτούς τους μήνες πριν τις Πανελλήνιες, οι νέοι εξασκούνται στη διαχείριση "περίεργων" προβλημάτων και λιγότερο στην κατανόηση των εννοιών.

Christos75 έγραψε:Καλησπέρα σε όλους. Να εκφράσω κι εγώ την άποψή μου για τα φετινά θέματα. Θεωρώ ότι με δεδομένη την συγκεκριμένη φετινή ύλη τα θέματα ήταν...καλά! Άλλωστε τι επιλογές υπήρχαν; Η διαβάθμιση ήταν σαφής και ξεκάθαρα με εξαίρεση τα θέματα Γ και Δ. Προσωπικά εγώ θεωρώ ότι οι δυσκολίες ξεκινούσαν από το θέμα Γ και συγκεκριμένα το Γ2 και υπήρχε πρόβλημα στην αντιμετώπιση και του Γ4 από αρκετά παιδιά. Ωστόσο, θεωρώ ότι το 14 με 16 είναι εφικτό και από ένα μέτριο μαθητή αλλά από εκεί και πάνω τα πράγματα ήταν δύσκολα και απαιτούσαν καθαρό μυαλό, τεχνικές και εμβάθυνση στην ύλη, καλώς για εμένα. Το πρόβλημα που εγώ θέλω να εκφράσω και να επαναφέρω με δεδομένη τη σημερινή εξέταση είναι ότι πρέπει να αλλάξουμε τη ρότα που έχουν πάρει τα Μαθηματικά τον τελευταίο χρόνο. Κατ'εμέ δεν είναι δυνατόν να έχουμε στην ύλη Μ Ο Ν Ο ανάλυση και άλλους τομείς των Μαθηματικών ούτε καν τους...«ακουμπάμε». Που είναι η Άλγεβρα; Η Γεωμετρία ίσως; Δεν είναι δυνατόν η μαθηματική μας κουλτούρα να περιορίζεται στην Ανάλυση και σε εξετάσεις εισαγωγής σε πανεπιστήμια να προσπαθούμε να βάλουμε «τεχνικά» θέματα, λεπτομέρειες ανούσιες και παγίδες για να πέσει μέσα ο κόσμος! Πρέπει σαφώς και ξεκάθαρα, η ύλη των Μαθηματικών να διευρυνθεί, να υπάρχει επέκταση και σε άλλους τομείς και ας μην έχει τόσο βάθος στην εξέτασή της αλλά...ευρύτητα γνώσεων! Η συρρίκωνση που υφίσταται το εν λόγω μαθημα είναι ε γ κ λ η μ α τ ι κ ή ! ! ! Η Ελληνική Μαθηματική Εταιρία (Ε.Μ.Ε.) αλλά και όλοι εμείς που αγαπάμε το αντικείμενο πρέπει να αλλάξουμε αυτή τη στρέβλωση στον επιστημονικό αυτό χώρο. Ελπίζω να μην κούρασα με όσα ανέφερα και να δούμε σύντομα αλλαγές που να είναι προς όφελος της Μαθηματικής παιδείας της χώρας μας.

mathematica · #123

Καλημέρα σας
Νομίζω πως στην παρούσα φάση (εν μέσω εξετάσεων) ,θα πρέπει να αρκεστούμε στο προφανές. Τα θέματα ήταν σαφώς διατυπωμένα, υπήρχε κλιμάκωση δυσκολίας ώστε να υπάρξει η απαιτούμενη κατανομή στη βαθμολογία, εξέλειπαν φρικαλέα λάθη από πλευράς μαθηματικής ορθότητας και ευτυχώς για τους υποψήφιους , φαίνεται πως τα μέλη της επιτροπής έδειξαν την απαραίτητη εγκράτεια ώστε να μην προτείνουν ακαλαίσθητες , επιδεικτικές μαθηματικές υπερκατασκευές που έχουμε συναντήσει κατά το παρελθόν.
Καλή συνέχεια στους υποψηφίους και σε όλους τους συναδέλφους , φίλους παλιούς και νέους.
Πολλάτος Γεράσιμος
Μαθηματικός (νομίζω)

#124

mathematica έγραψε:Καλημέρα σας
Νομίζω πως στην παρούσα φάση (εν μέσω εξετάσεων) ,θα πρέπει να αρκεστούμε στο προφανές. Τα θέματα ήταν σαφώς διατυπωμένα, υπήρχε κλιμάκωση δυσκολίας ώστε να υπάρξει η απαιτούμενη κατανομή στη βαθμολογία, εξέλειπαν φρικαλέα λάθη από πλευράς μαθηματικής ορθότητας και ευτυχώς για τους υποψήφιους , φαίνεται πως τα μέλη της επιτροπής έδειξαν την απαραίτητη εγκράτεια ώστε να μην προτείνουν ακαλαίσθητες , επιδεικτικές μαθηματικές υπερκατασκευές που έχουμε συναντήσει κατά το παρελθόν.

Ναι, αλλά τα προβλήματα εξακολουθούν να μην έχουν 'ουσία' και ενδιαφέρον, εκφράζει ας πούμε κάποια βαθύτερη αλήθεια το Γ4; Πόσο θα μας ενδιέφερε ως αποτέλεσμα ... αν δεν ήταν θέμα εξετάσεων; [Φυσικά αυτό το ερώτημα θα μπορούσε να τεθεί σχεδόν για κάθε θέμα που μπορεί να φανταστεί κανείς, "έξω από τον χορό πολλά τραγούδια λέμε", κλπ]

nikolaos p. · #125

Christos75 έγραψε:........................................................................
Το πρόβλημα που εγώ θέλω να εκφράσω και να επαναφέρω με δεδομένη τη σημερινή εξέταση είναι ότι πρέπει να αλλάξουμε τη ρότα που έχουν πάρει τα Μαθηματικά τον τελευταίο χρόνο. Κατ'εμέ δεν είναι δυνατόν να έχουμε στην ύλη Μ Ο Ν Ο ανάλυση και άλλους τομείς των Μαθηματικών ούτε καν τους...«ακουμπάμε». Που είναι η Άλγεβρα; Η Γεωμετρία ίσως; Δεν είναι δυνατόν η μαθηματική μας κουλτούρα να περιορίζεται στην Ανάλυση και σε εξετάσεις εισαγωγής σε πανεπιστήμια να προσπαθούμε να βάλουμε «τεχνικά» θέματα, λεπτομέρειες ανούσιες και παγίδες για να πέσει μέσα ο κόσμος! Πρέπει σαφώς και ξεκάθαρα, η ύλη των Μαθηματικών να διευρυνθεί, να υπάρχει επέκταση και σε άλλους τομείς και ας μην έχει τόσο βάθος στην εξέτασή της αλλά...ευρύτητα γνώσεων! Η συρρίκωνση που υφίσταται το εν λόγω μαθημα είναι ε γ κ λ η μ α τ ι κ ή ! ! ! Η Ελληνική Μαθηματική Εταιρία (Ε.Μ.Ε.) αλλά και όλοι εμείς που αγαπάμε το αντικείμενο πρέπει να αλλάξουμε αυτή τη στρέβλωση στον επιστημονικό αυτό χώρο. Ελπίζω να μην κούρασα με όσα ανέφερα και να δούμε σύντομα αλλαγές που να είναι προς όφελος της Μαθηματικής παιδείας της χώρας μας.

Συμφωνώ απόλυτα!

S.E.Louridas · #126

gbaloglou έγραψε:
mathematica έγραψε:Καλημέρα σας
Νομίζω πως στην παρούσα φάση (εν μέσω εξετάσεων) ,θα πρέπει να αρκεστούμε στο προφανές. Τα θέματα ήταν σαφώς διατυπωμένα, υπήρχε κλιμάκωση δυσκολίας ώστε να υπάρξει η απαιτούμενη κατανομή στη βαθμολογία, εξέλειπαν φρικαλέα λάθη από πλευράς μαθηματικής ορθότητας και ευτυχώς για τους υποψήφιους , φαίνεται πως τα μέλη της επιτροπής έδειξαν την απαραίτητη εγκράτεια ώστε να μην προτείνουν ακαλαίσθητες , επιδεικτικές μαθηματικές υπερκατασκευές που έχουμε συναντήσει κατά το παρελθόν.
Ναι, αλλά τα προβλήματα εξακολουθούν να μην έχουν 'ουσία' και ενδιαφέρον, εκφράζει ας πούμε κάποια βαθύτερη αλήθεια το Γ4; Πόσο θα μας ενδιέφερε ως αποτέλεσμα ... αν δεν ήταν θέμα εξετάσεων; [Φυσικά αυτό το ερώτημα θα μπορούσε να τεθεί σχεδόν για κάθε θέμα που μπορεί να φανταστεί κανείς, "έξω από τον χορό πολλά τραγούδια λέμε", κλπ]

Ναί Γιώργο πράγματι.

Επιτρέψτε μου να θεωρώ παράξενο τον κάθε "πανηγυρισμό" ότι στο κορυφαίο διαγωνισμό επιλογής των φοιτητών μας αποτελεί γεγονός το ότι δεν υπάρχει Μαθηματικό λάθος. Εκεί φτάσαμε; Τα φετινά θέματα ήταν θέματα καθαρά φροντιστηριακής νοοτροπίας (το αναφέρω επισημαίνοντας και όχι καταδεικνύοντας, αφού θεωρώ την φροντιστηριακή εκπαίδευση θετική και αναγκαία στη Πατρίδα μας) που οι λύσεις τους είναι καθαρά θέμα τεχνικών. Για παράδειγμα στα φροντιστήρια λέμε και μάλιστα με φροντιστηριακή έμφαση: Σου δίνει συνεχή συνάρτηση και τουλάχιστον μία τιμή τιμή της διάφορη του μηδενός; .... Τότε κοίτα την διατήρηση του πρόσημου. Και συμπληρώνουμε με έμφαση: ... μη παρασυρθήτε από το εμφανισιακό μέρος της που ίσως πάνε να σε μπλέξουν, εσύ αυτό θα κοιτάς για την συνεχή

ή για την συνεχή f{'}

ή ... για την συνεχή $f^\ (n)$ κτλ. Προσωπικά και εγώ και ο άλλος συνάδελφος που διδάσκουμε στο αλληλέγγυο του Δήμου μας το είχαμε διδάξει και είχαμε βάλει και διαγώνισμα στην νοοτροπία αυτή. Το Δ' θέμα δεν στηρίζεται εκεί; Καλά καθαρά θέματα απλής κατασκευαστικής νοοτροπίας (επιλέγω π.χ. την f(x)=x

κτίζω μία συναρτησιακή μειώνοντας το ενδεχόμενο να ανακαλυφθεί μέσω αυτής ο τύπος της και ...να το θέμα μου), αλλά θέματα που μπορεί να επιλυθούν έτσι ή αλλιώς. Στο μέλλον καλό θα είναι οι θεματοδότες να αρχίζουν να κατασκευάζουν ή να επιλέγουν θέματα που να ανιχνεύουν την σε βάθος κατανόηση της Θεωρίας, ώστε η επιλογή της μεθόδου επίλυσης να επαφίεται στον κάθε λύτη και την αυτενέργεια του.
Ειλικρινή Συγχαρητήρια στους Διαγωνιζόμενους και στους διδάσκοντες τους και καλά αποτελέσματα.

(*) Υπάρχει άραγε διδάσκων που να μην έχει διδάξει την $e^x\geq x+1$ και την nini απόδειξη της, ώστε να χρησιμοποιείται "αυτομάτως" και άμα τη εμφανίσει της σε θέμα; Ποτέ δεν κατανόησα γιατί το επίσημο βιβλίο την $e^x\geq x+1$ την ..."κρύβει" ως εφαρμογή της θεωρίας και τη μετατοπίζει σε άσκηση.

edit: Τοποθέτηση της (*).

#127

Σε ποιο θέμα ακριβώς υπεισέρχονται
τα Μαθηματικά προσανατολισμού της Β΄ ;

knkn · #128

Η εκτίμησή μου είναι ότι τα φετινά θέματα εξυπηρετούν τον σκοπό για τον οποίο έχουν δημιουργηθεί . Όταν θα έχουμε τα στατιστικά στοιχεία της επίδοσης των μαθητών θα έχουμε καλύτερη εικόνα φυσικά .

Christos.N · #129

exdx έγραψε:Σε ποιο θέμα ακριβώς υπεισέρχονται
τα Μαθηματικά προσανατολισμού της Β΄ ;

Αυτό Γιώργη ξανά πες το ...Ταφόπλακα μεγάλη δυστυχώς, κρίμα...

Kostas Tzimoulias · #130

Εγώ ώς μαθητής για κακή μου τύχη επειδή πάντα στις διαφορικές αυτές εξισώσεις κοιτάω αν μπορώ να βρώ μια προφανή συνάρτηση. Χθες δεν είδα ότι ο όρος ήταν f(f(x))

και απο απροσεξία έιδα οτι ήταν f(x)

παρασυρόμενος απο αυτή τη βλακεία με λάθος τρόπο απέδειξα ότι η συνάρτηση ήταν η f(x)=x

και Δ2,Δ3,Δ3 πήγαν κατα διαόλου...σωστά θα ήταν αν είχα αποδείξει με σωστό τρόπο τη συνάρτηση αλλά δε τα κατάφερα και ούτε νομίζω θα τα κατάφερνα αφού ο χρόνος να συλλάβω την ιδέα και να την αποδείξω δε μου έφτανε. Εκει που υπολόγιζα δηλαδή να χάσω απο το Γ2 ( επειδή βρήκα 2 συναρτησεις) και απο το Γ4 επειδη δεν πήρα δευτερη περιπτωση για το ΘΜΤ κατέληξα να πάρω μηδεν σε 3 ερωτηματα...και απο ένα 18 και γιατί όχι και 18,8 που υπολόγιζα είμαι στο 15.5 με το ζόρι..υπάρχει μια περίπτωση να πάρω έστω λίγα μόρια στα 3 αυτά ερωτήματα? φοβάμαι μην ο βαθμολογητής νομίζει οτι πήγα να τον κοροιδέψω με αυτή τη λανθασμένη απόδειξη. τα χειρότερα συμβαίνουν εκεί που δε τα περιμένεις τελικά

Xer · #131

Μια ερώτηση για το γ3. Εάν θέταμε $\displaystyle{υ=x^2}$ η συνάρτηση f(u)

είχε πεδίο ορισμού το $\displaystyle{(0,+\infty),}$ και με δυο παραγωγισεις έβγαινε η κυρτότητα στο νέο πεδίο ορισμού. Θεωρείται σωστο;

#132

Xer έγραψε:Μια ερωτηση για το γ3. Εάν θέταμε υ=χ^2 η συνάρτηση f(u) ειχε πεδίο ορισμού το 0,+άπειρο, και με δυο παραγωγισεις έβγαινε η κυρτότητα στο νέο πεδίο ορισμού. Θεωρείται σωστο;

Δεν είναι σωστό. Πέρα από το ότι αλλάζει το πεδίο ορισμού, ακόμη και στην περίπτωση που είναι ίδιο θα είχαμε πρόβλημα. Πάρε για παράδειγμα τη συνάρτηση $f(x)=x^4-x^2, \ x\geq 0$ με αντίστοιχη την $g(x)=x^2-x, \ x\geq 0$ .

Αλέξανδρος

Xer · #133

cretanman έγραψε:
Xer έγραψε:Μια ερωτηση για το γ3. Εάν θέταμε υ=χ^2 η συνάρτηση f(u) ειχε πεδίο ορισμού το 0,+άπειρο, και με δυο παραγωγισεις έβγαινε η κυρτότητα στο νέο πεδίο ορισμού. Θεωρείται σωστο;
Δεν είναι σωστό. Πέρα από το ότι αλλάζει το πεδίο ορισμού, ακόμη και στην περίπτωση που είναι ίδιο θα είχαμε πρόβλημα. Πάρε για παράδειγμα τη συνάρτηση $f(x)=x^4-x^2, \ x\geq 0$ με αντίστοιχη την $g(x)=x^2-x, \ x\geq 0$ .

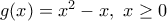Αλέξανδρος

Το πεδίο ορισμού αλλάζει αλλα δεν υπαρχει θεμα γιατι δημιουργείται μια νεα συνάρτηση που ειναι κυρτή στο δικό της πεδίο ορισμού.

Λάμπρος Μπαλός · #134

Xer έγραψε:Μια ερωτηση για το γ3. Εάν θέταμε υ=χ^2 η συνάρτηση f(u) ειχε πεδίο ορισμού το 0,+άπειρο, και με δυο παραγωγισεις έβγαινε η κυρτότητα στο νέο πεδίο ορισμού. Θεωρείται σωστο;

Εννοείς πως αν θέσεις $y=x^{2}$ θα προκύψει $f(y)=e^{y}-y-1$ ;

Αν ναι, μην ξεχνάς ότι θέτοντας $y=x^{2}$ προκύπτει $f(\sqrt{y})=e^{y}-y-1$ και αυστηρά στο $[0,+ \infty)$

υγ..πέραν αυτού, ένα τέτοιου είδους θέσιμο δεν είναι πάντα σωστό.

Λάμπρος Μπαλός · #135

Μια ερώτηση..

Αν τα ερωτήματα Δ2α,Δ2β είχαν την ανάποδη σειρά, ποιά είναι η λύση που θα προτείνατε; Κάνω την ερώτηση και εκφράζω ταυτόχρονα την απορία..μπας και υπήρξαν μαθητές που απαντήσανε πρώτα στο β και έπειτα στο α;

nickos_m · #136

Καλησπέρα σας.
Ως μαθητής εκφέρω την άποψη ότι τα θέματα ήταν "καλά" για τους διαβασμένους μαθητές, καθώς μου φάνηκαν ... τυποποιημένα!Δεν χρειάστηκε πουθενά η χρήση κριτικής σκέψης.Αυτό ,βέβαια, δεν πάει να πει ότι προτιμούμε τα θέματα άλλων ετών.
Ήθελα να δω τι ακριβώς έχω γράψει αφού έχουν τελειώσει όλα τα μαθήματα,αλλά ύστερα από ατελείωτες ερωτήσεις από φίλους και γνωστούς υπέκυψα στον πειρασμό να προσδιορίσω στο περίπου τα μόρια που "έπιασα".
Α,Β,Γ θέματα όλα okay.
Όσον αφορά το Δ έχω κάποιες απορίες:
Δ1)Όλα okay.
Δ2)α)okay
β)Έγραψα πως επειδή η f(x)

είναι συνεχής και δεν παρουσιάζει ακρότατα στο

τότε θα είναι γνησίως μονότονη και ,επιπλέον, επειδή είναι $0<\pi \Leftrightarrow f(0)<f(\pi )$ τότε θα είναι γνησίως αύξουσα.Το συγκεκριμένο ερώτημα έπιανε 2 μόρια.Υπάρχει η πιθανότητα να πάρω τουλάχιστον το 1;
Δ3)Παρατηρώ στο site ότι γράφεται $cosx + sinx \leq 2$ και στη συνέχεια το φράζουν.Ξεκίνησα με αυτήν την σκέψη αλλά δεν την συνέχισα αφού η συγκεκριμένη ανισότητα δεν μπορεί να πάρει την τιμή

αλλά μία κοντά στο 1,7

.Επομένως, το έσπασα σε δύο όρια (και αφού έγραψα ότι τα επιμέρους όρια υπάρχουν) και τα έφραξα.Είναι σωστό;
Δ4)Όσο κι αν προσπαθούσα αλλαγή μεταβλητής ,δυστυχώς, δεν μπορούσα να τη δω.
Αρχικά έκανα την απόδειξη ότι αν δύο συναρτήσεις g,h

είναι συνεχής σε ένα κλειστό διάστημα [a,b]

και ισχύει $g(x)\geq h(x) \forall x \in [a,b]$ τότε θα είναι $\int_{a}^{b}{g(x)dx}>\int_{a}^{b}{h(x)dx}$ .
Έπειτα είπα: για $1\leq lnx \leq e^{\pi } \Leftrightarrow ... \Leftrightarrow \int_{1}^{e^{\pi }}{\frac{f(1)}{x}dx} < \int_{1}^{e^{\pi }}{\frac{f(lnx)}{dx}} < \int_{1}^{e^{\pi }}{\frac{f(e^{\pi })}{x}dx}$
Όμως, $f(1)\pi > 0 \Leftrightarrow \int_{1}^{e^{\pi }}{\frac{f(lnx)}{dx}} > 0$ .
Πόσα μόρια στα 6 πιστεύετε μπορεί να πάρω;

p.s.(1)-Σας ευχαριστώ εκ των προτέρων.
p.s.(2)-Καλή τύχη στα υπόλοιπα μαθήματα στους συμμαθητές μου.

NikosTheodorakis · #137

nickos_m έγραψε:Καλησπέρα σας.
Ως μαθητής εκφέρω την άποψη ότι τα θέματα ήταν "καλά" για τους διαβασμένους μαθητές, καθώς μου φάνηκαν ... τυποποιημένα!Δεν χρειάστηκε πουθενά η χρήση κριτικής σκέψης.Αυτό ,βέβαια, δεν πάει να πει ότι προτιμούμε τα θέματα άλλων ετών.
Ήθελα να δω τι ακριβώς έχω γράψει αφού έχουν τελειώσει όλα τα μαθήματα,αλλά ύστερα από ατελείωτες ερωτήσεις από φίλους και γνωστούς υπέκυψα στον πειρασμό να προσδιορίσω στο περίπου τα μόρια που "έπιασα".
Α,Β,Γ θέματα όλα okay.
Όσον αφορά το Δ έχω κάποιες απορίες:
Δ1)Όλα okay.
Δ2)α)okay
β)Έγραψα πως επειδή η είναι συνεχής και δεν παρουσιάζει ακρότατα στο τότε θα είναι γνησίως μονότονη και ,επιπλέον, επειδή είναι $0<\pi \Leftrightarrow f(0)<f(\pi )$ τότε θα είναι γνησίως αύξουσα.Το συγκεκριμένο ερώτημα έπιανε 2 μόρια.Υπάρχει η πιθανότητα να πάρω τουλάχιστον το 1;
Δ3)Παρατηρώ στο site ότι γράφεται $cosx + sinx \leq 2$ και στη συνέχεια το φράζουν.Ξεκίνησα με αυτήν την σκέψη αλλά δεν την συνέχισα αφού η συγκεκριμένη ανισότητα δεν μπορεί να πάρει την τιμή αλλά μία κοντά στο .Επομένως, το έσπασα σε δύο όρια (και αφού έγραψα ότι τα επιμέρους όρια υπάρχουν) και τα έφραξα.Είναι σωστό;
Δ4)Όσο κι αν προσπαθούσα αλλαγή μεταβλητής ,δυστυχώς, δεν μπορούσα να τη δω.
Αρχικά έκανα την απόδειξη ότι αν δύο συναρτήσεις είναι συνεχής σε ένα κλειστό διάστημα και ισχύει $g(x)\geq h(x) \forall x \in [a,b]$ τότε θα είναι $\int_{a}^{b}{g(x)dx}>\int_{a}^{b}{h(x)dx}$ .
Έπειτα είπα: για $1\leq lnx \leq e^{\pi } \Leftrightarrow ... \Leftrightarrow \int_{1}^{e^{\pi }}{\frac{f(1)}{x}dx} < \int_{1}^{e^{\pi }}{\frac{f(lnx)}{dx}} < \int_{1}^{e^{\pi }}{\frac{f(e^{\pi })}{x}dx}$
Όμως, $f(1)\pi > 0 \Leftrightarrow \int_{1}^{e^{\pi }}{\frac{f(lnx)}{dx}} > 0$ .
Πόσα μόρια στα 6 πιστεύετε μπορεί να πάρω;
p.s.(1)-Σας ευχαριστώ εκ των προτέρων.
p.s.(2)-Καλή τύχη στα υπόλοιπα μαθήματα στους συμμαθητές μου.

Δ2 β) Θα έδινα το 1 από τα 2 μόρια, αλλά άλλος μπορεί να σε βαθμολογούσε διαφορετικά.
Δ3 Με το σκεπτικό που το πας καλό είναι πρώτα να υπολογίσεις ξεχωριστά τα δύο όρια και υπολογίζοντάς τα στην ουσία δείχνεις ότι υπάρχουν, άρα μετά μπορείς να σπάσεις το αρχικό όριο σε δύο, αφού υπάρχουν τα επιμέρους και να το υπολογίσεις. Αν το έγραψες όπως είπα θα σου έβαζα 6 στα 6 μόρια.
Δ4 Το τελευταίο όπως το γράφεις δεν είναι σωστό, εκτός και αν έγινε τυπογραφικό και εννοείς:

$1\leq lnx \leq e^{\pi } \Leftrightarrow ... \rightarrow \int_{1}^{e^{\pi }}{\frac{f(1)}{x}dx} < \int_{1}^{e^{\pi }}{\frac{f(lnx)}{x}dx} < \int_{1}^{e^{\pi }}{\frac{f(e^{\pi })}{x}dx}$
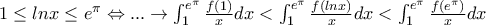
Όμως, $f(1)\pi > 0 \rightarrow \int_{1}^{e^{\pi }}{\frac{f(lnx)}{x}dx} > 0$ .

Επίσης προσοχή, όταν ολοκληρώνεις σε ανισότητα δεν ισχύει το αντίστροφο, πρέπει να βάλλεις συνεπαγωγή και όχι ισοδυναμία! Αν το έγραψες όπως και εγώ παραπάνω στην ουσία απέδειξες τη μία από τις δύο ανισότητες, οπότε παίρνεις 3 από τα 6.

Καλή συνέχεια και καλή επιτυχία στα υπόλοιπα, τα πήγες αρκετά καλά πάντως μπράβο!

Y.Γ.στην απόδειξη που έκανες στο Δ4 πρέπει να αναφέρεις και ότι οι συναρτήσεις δεν είναι παντού ίσες, ώστε να καταλήξεις σε γνήσια ανισότητα από "ανισοϊσότητα¨.

Stateofmind · #138

nickos_m έγραψε:Καλησπέρα σας.
Ως μαθητής εκφέρω την άποψη ότι τα θέματα ήταν "καλά" για τους διαβασμένους μαθητές, καθώς μου φάνηκαν ... τυποποιημένα!Δεν χρειάστηκε πουθενά η χρήση κριτικής σκέψης.Αυτό ,βέβαια, δεν πάει να πει ότι προτιμούμε τα θέματα άλλων ετών.
Ήθελα να δω τι ακριβώς έχω γράψει αφού έχουν τελειώσει όλα τα μαθήματα,αλλά ύστερα από ατελείωτες ερωτήσεις από φίλους και γνωστούς υπέκυψα στον πειρασμό να προσδιορίσω στο περίπου τα μόρια που "έπιασα".
Α,Β,Γ θέματα όλα okay.
Όσον αφορά το Δ έχω κάποιες απορίες:
Δ1)Όλα okay.
Δ2)α)okay
β)Έγραψα πως επειδή η είναι συνεχής και δεν παρουσιάζει ακρότατα στο τότε θα είναι γνησίως μονότονη και ,επιπλέον, επειδή είναι $0<\pi \Leftrightarrow f(0)<f(\pi )$ τότε θα είναι γνησίως αύξουσα.Το συγκεκριμένο ερώτημα έπιανε 2 μόρια.Υπάρχει η πιθανότητα να πάρω τουλάχιστον το 1;
Δ3)Παρατηρώ στο site ότι γράφεται $cosx + sinx \leq 2$ και στη συνέχεια το φράζουν.Ξεκίνησα με αυτήν την σκέψη αλλά δεν την συνέχισα αφού η συγκεκριμένη ανισότητα δεν μπορεί να πάρει την τιμή αλλά μία κοντά στο .Επομένως, το έσπασα σε δύο όρια (και αφού έγραψα ότι τα επιμέρους όρια υπάρχουν) και τα έφραξα.Είναι σωστό;
Δ4)Όσο κι αν προσπαθούσα αλλαγή μεταβλητής ,δυστυχώς, δεν μπορούσα να τη δω.
Αρχικά έκανα την απόδειξη ότι αν δύο συναρτήσεις είναι συνεχής σε ένα κλειστό διάστημα και ισχύει $g(x)\geq h(x) \forall x \in [a,b]$ τότε θα είναι $\int_{a}^{b}{g(x)dx}>\int_{a}^{b}{h(x)dx}$ .
Έπειτα είπα: για $1\leq lnx \leq e^{\pi } \Leftrightarrow ... \Leftrightarrow \int_{1}^{e^{\pi }}{\frac{f(1)}{x}dx} < \int_{1}^{e^{\pi }}{\frac{f(lnx)}{dx}} < \int_{1}^{e^{\pi }}{\frac{f(e^{\pi })}{x}dx}$
Όμως, $f(1)\pi > 0 \Leftrightarrow \int_{1}^{e^{\pi }}{\frac{f(lnx)}{dx}} > 0$ .
Πόσα μόρια στα 6 πιστεύετε μπορεί να πάρω;

p.s.(1)-Σας ευχαριστώ εκ των προτέρων.
p.s.(2)-Καλή τύχη στα υπόλοιπα μαθήματα στους συμμαθητές μου.

Στο Δ2 Β είπα σχεδόν το ίδιο απλά είπα ότι αποκλείεται να είναι γν. Φθίνουσα και επειδή είναι γν. Μονότονη θα είναι γν. Αύξουσα, βέβαια δεν ανέφερα τη συνέχεια λόγω υπόθεσης. Κάτι τέτοιο όμως απαιτεί απόδειξη. Αν πέσουμε σε καλή περίπτωση βαθμολογητή ίσως πάρουμε το ένα μόριο. Στο Δ3 αιτιολογώντας πως βρήκα το όριο της f στο +άπειρο και λέγοντας ότι είναι θετική κοντά σε αυτό έσπασα το κλάσμα σε 2 και μέσω κριτηρίου παρεμβολής το έλυσα και δεν βρίσκω λόγο να είναι λάθος. Καλή συνέχεια

#139

cretanman έγραψε:
GiorgosSim έγραψε:
cretanman έγραψε:Εναλλακτικός τρόπος για το Γ4

Θα δείξουμε ότι η είναι μοναδική λύση της εξίσωσης.

Υποθέτουμε λοιπόν, αντίθετα, ότι υπάρxει που να είναι λύση της εξίσωσης. Ισxύει $|\eta\mu x_0|<x_0$ (από τη γνωστή ανισότητα $|\eta\mu x|\leq |x|$ με ισότητα μόνο για ) καθώς επίσης $|\eta\mu x_0|< |\eta\mu x_0|+3$ και .

Διακρίνουμε τις περιπτώσεις:

$\bullet$ Αν $|\eta\mu x_0|+3<x_0$ τότε $|\eta\mu x_0|< |\eta\mu x_0|+3<x_0<x_0+3$ και επειδή ισxύουν οι προϋποθέσεις του ΘΜΤ σε κάθε ένα από τα διαστήματα $\left[|\eta\mu x_0|, |\eta\mu x_0|+3\right], \ \left[x_0,x_0+3\right]$ άρα υπάρxουν $\xi_1 \in \left(|\eta\mu x_0|, |\eta\mu x_0|+3\right) , \ \xi_2 \in \left(x_0,x_0+3\right)$ ώστε η εξίσωση να γράφεται:

$3f'(\xi_1)=3f'(\xi_2)$ απ΄όπου $f'(\xi_1)=f'(\xi_2)$ και αφού η είναι γνησίως αύξουσα (ως κυρτή) άρα είναι και κι έτσι παίρνουμε $\xi_1=\xi_2$ , πράγμα άτοπο αφού τα $\xi_1, \xi_2$ ανήκουν σε διαφορετικά διαστήματα.

$\bullet$ Αν $x_0\leq |\eta\mu x_0|+3$ τότε $|\eta\mu x_0|<x_0\leq |\eta\mu x_0|+3<x_0+3$ .

Γράφουμε την εξίσωση στη μορφή: $f(x_0)-f\left(|\eta\mu x_0|\right)=f(x_0+3)-f\left(|\eta\mu x_0|+3\right)$

Επειδή ισxύουν οι προϋποθέσεις του ΘΜΤ σε κάθε ένα από τα διαστήματα $\left[|\eta\mu x_0|, x_0\right], \ \left[|\eta\mu x_0|+3, x_0+3\right]$ άρα υπάρxουν $\xi_1 \in \left(|\eta\mu x_0|, x_0) , \ \xi_2 \in \left(|\eta\mu x_0|+3, x_0+3\right)$ ώστε η εξίσωση να γράφεται:

$(x_0-|\eta\mu x_0|)f'(\xi_1)=(x_0-|\eta\mu x_0|)f'(\xi_2)$ και αφού $x_0-|\eta\mu x_0|\neq 0$ άρα $f'(\xi_1)=f'(\xi_2)$ και αφού η είναι γνησίως αύξουσα (ως κυρτή) άρα είναι και , κι έτσι παίρνουμε $\xi_1=\xi_2$ , πράγμα άτοπο αφού τα $\xi_1, \xi_2$ ανήκουν σε διαφορετικά διαστήματα.

Χαιρετώ την αγαπητή παρέα του . Ολόιδια ακριβώς λύση με τον κ. Cretaman έκανα. Απλά έχω ενδοιασμούς μήπως υπάρχει κάποιο πρόβλημα στα διαστήματα και μπλέκονται σε κάποια περίπτωση.
Δεν τίθεται τέτοιο θέμα. Αυτός είναι και ο λόγος που παίρνουμε περιπτώσεις (στη δεύτερη περίπτωση τροποποιούμε και την εξίσωση): Για να μην έχουμε αλληλοεπικάλυψη διαστημάτων και έτσι να καταλήξουμε σε άτοπο.

Αλέξανδρε νομίζω, σε σχέση και με το ερώτημα φίλου μαθηματικού που δεν γράφει στο

, ότι ο παραπάνω συλλογισμός σου μπορεί να επεκταθεί στο εξής:

Αν A, B, C, D

είναι σημεία πάνω στο γράφημα κυρτής συνάρτησης τέτοια ώστε $A\prec B\prec C\prec D$ ή $A\prec C\prec B\prec D$ τότε η κλίση του

είναι μικρότερη της κλίσης του

.

Στο συνημμένο σκιαγραφείται μία γεωμετρική απόδειξη που δείχνει ότι το συμπέρασμα μπορεί να ισχύει ακόμη και στην περίπτωση $A\prec C\prec D\prec B$ , υπό τον όρο να ισχύει και η $C'\prec D$ , όπου

το μοναδικό επί του γραφήματος σημείο τέτοιο ώστε CC'//AB

.

nks · #140

Επιτροπή Θεμάτων 16 έγραψε:Δημοσιεύουμε την 1η Έκδοση του Δελτίου Λύσεων του στη σημερινή εξέταση των μαθητών στα Μαθηματικά που επιμελήθηκαν τα Διευθύνοντα Μέλη του mathematica.

Δόθηκε ιδιαίτερη έμφαση στις εναλλακτικές προσεγγίσεις κάποιων επιμέρους ερωτημάτων με σκοπό τη διευκόλυνση και των συναδέλφων Βαθμολογητών των οποίων το δύσκολο έργο ξεκινά μεθαύριο. Οι εναλλακτικοί τρόποι βρίσκονται στο τέλος του Δελτίου.

Τυχόντα τυπογραφικά/λάθη ή εναλλακτικές προσεγγίσεις σε κάποια ερωτήματα (μόνο αν διαφέρουν στην ουσία της λύσης και όχι στον τρόπο γραφής) μπορείτε να τα στέλνετε με προσωπικό μήνυμα στον παρόντα λογαριασμό είτε με email στο info (AT) mathematica.gr

Ευχόμαστε καλή συνέχεια στους μαθητές μας που διαγωνίστηκαν και καλά αποτελέσματα!

Εκ μέρους της επιτροπής σύνταξης του Δελτίου Λύσεων

MATHEMATICA GR Μαθ Θετ κατ Λύσεις Θεμάτων 2016(Έκδοση 1).pdf

Στο Θέμα Δ4 εγώ έδωσα άλλη λύση.
Διαίρεσα αριθμητή και παρονομαστή με x οπότε θα αριθμητής με κριτήριο παρεμβολής είναι 0 και ο παρονομαστής με de l'hospital έβγαλα ότι είναι αριθμός διάφορος του μηδενός γιατί ξέρουμε ότι f'(x)>0.
Δηλαδή τελικά ολόκληρο το όριο κάνει 0.
Δεν είναι σωστό;

Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Re: Μαθηματικά προσαν. (κατεύθ.) 2016

Μέλη σε σύνδεση