Μαθηματικά Γενικής Παιδείας 2015
-
Επιτροπή Θεμάτων 15
- Δημοσιεύσεις: 8
- Εγγραφή: Τετ Μάιος 20, 2015 9:51 am
Μαθηματικά Γενικής Παιδείας 2015
Αγαπητές/τοί φίλες/οι
Στο θέμα αυτό αποκλειστικά θα συζητήσουμε τα θέματα των Μαθηματικών Γενικής Παιδείας 2015 αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου.
Στο θέμα αυτό αποκλειστικά θα συζητήσουμε τα θέματα των Μαθηματικών Γενικής Παιδείας 2015 αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου.
Επιτροπή Θεμάτων 2015
-
Επιτροπή Θεμάτων 15
- Δημοσιεύσεις: 8
- Εγγραφή: Τετ Μάιος 20, 2015 9:51 am
Re: Μαθηματικά Γενικής Παιδείας 2015
Τα θέματα που μόλις δημοσιεύθηκαν στη σελίδα του Υπουργείου.
- Συνημμένα
-
- them_mat_gen_c_hmer_no_150520.pdf
- (281.66 KiB) Μεταφορτώθηκε 667 φορές
Επιτροπή Θεμάτων 2015
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Μαθηματικά Γενικής Παιδείας 2015
Για το Α θέμα:
Α1) Απόδειξη σελίδα 31 σχολικού βιβλίου
Α2) Ορισμός σελίδα 22 σχολικού βιβλίου
Α3) Ορισμός σελίδα 87 σχολικού βιβλίου
Α4) α) Λ (σελίδα 31 σχολικού βιβλίου)
β) Σ (σελίδα 14 σχολικού βιβλίου)
γ) Λ (σελίδα 95 σχολικού βιβλίου)
δ) Λ (σελίδα 97 σχολικού βιβλίου)
ε) Σ (σελίδα 141 σχολικού βιβλίου)
Ερωτήσεις για πολύ προσεκτικούς και καλοδιαβασμένους μαθητές όμως μέσα στο πλαίσιο του σχολικού βιβλίου.
Αλέξανδρος
Α1) Απόδειξη σελίδα 31 σχολικού βιβλίου
Α2) Ορισμός σελίδα 22 σχολικού βιβλίου
Α3) Ορισμός σελίδα 87 σχολικού βιβλίου
Α4) α) Λ (σελίδα 31 σχολικού βιβλίου)
β) Σ (σελίδα 14 σχολικού βιβλίου)
γ) Λ (σελίδα 95 σχολικού βιβλίου)
δ) Λ (σελίδα 97 σχολικού βιβλίου)
ε) Σ (σελίδα 141 σχολικού βιβλίου)
Ερωτήσεις για πολύ προσεκτικούς και καλοδιαβασμένους μαθητές όμως μέσα στο πλαίσιο του σχολικού βιβλίου.
Αλέξανδρος
Αλέξανδρος Συγκελάκης
Re: Μαθηματικά Γενικής Παιδείας 2015
Θέμα Δ.
Δ.1 Η κάθε διαγώνιος του ορθογωνίου είναι διάμετρος του κύκλου άρα έχει μήκος .
.
Άρα το πυθαγόρειο θεώρημα π.χ. στο τρίγωνο δίνει
δίνει  .
.
Επομένως το εμβαδόν του ορθογωνίου είναι όπως θέλαμε.
όπως θέλαμε.
Προφανώς ισχύει αφού αναφερόμαστε σε μήκος ευθ. τμήματος και
αφού αναφερόμαστε σε μήκος ευθ. τμήματος και  επειδή το τμήμα αυτό είναι σίγουρα μικρότερο της διαμέτρου.
επειδή το τμήμα αυτό είναι σίγουρα μικρότερο της διαμέτρου.
(Δεν μπορεί να είναι ίσο με τη διάμετρο γιατί τότε το ορθογώνιο εκφυλίζεται σε ευθ. τμήμα).
Άρα το π.ο. της είναι το
είναι το  .
.
Δ.2 Από τη γνωστή ανισότητα παίρνουμε
παίρνουμε  .
.
Η τιμή αυτή επιτυγχάνεται όταν και φυσικά τότε ισχύει
και φυσικά τότε ισχύει  οπότε το σχήμα είναι τετράγωνο.
οπότε το σχήμα είναι τετράγωνο.
Με παραγώγους έχει λίγες παραπάνω πράξεις αλλά με παραγώγους θα το λύσουν οι περισσότεροι.
Δ.3 Θέτουμε και το όριο γίνεται
και το όριο γίνεται  .
.
Ισχύει άρα
άρα  .
.
Επομένως το ζητούμενο όριο ισούται με .
.
Δ.4 Μελετάμε την ως προς τη μονοτονία.Θα λύσουμε την ανίσωση
ως προς τη μονοτονία.Θα λύσουμε την ανίσωση 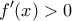 .
.
Ισοδύναμα θέλουμε .
.
Άρα στο διάστημα η
η  είναι γνησίως αύξουσα.Ισχύει
είναι γνησίως αύξουσα.Ισχύει  και
και ![\displaystyle{P(A),P(A-B)\in (0,1]\subset (0,5\sqrt{2})} \displaystyle{P(A),P(A-B)\in (0,1]\subset (0,5\sqrt{2})}](/forum/ext/geomar/texintegr/latexrender/pictures/45cfccdf3ce71e5dfaec80574e660814.png) .
.
Επομένως
 .
.
Επίσης και
και  .
.
Η τελευταία ισχύει αφού ισχύουν και οι και
και  οπότε η ζητούμενη προκύπτει με πολ/σμο κατά μέλη των παραπάνω.
οπότε η ζητούμενη προκύπτει με πολ/σμο κατά μέλη των παραπάνω.
Με λίγα λόγια η παράσταση ανήκει σίγουρα στο διάστημα
ανήκει σίγουρα στο διάστημα  ,το ίδιο και η
,το ίδιο και η  .
.
Στο διάστημα αυτό όμως η είναι γνησίως αύξουσα άρα η
είναι γνησίως αύξουσα άρα η  δίνει τη ζητούμενη ανισότητα.
δίνει τη ζητούμενη ανισότητα.
Edit:Πρόσθεσα τα πράσινα μετά από υπόδειξη του Χρ. Τσιφάκη.
Δ.1 Η κάθε διαγώνιος του ορθογωνίου είναι διάμετρος του κύκλου άρα έχει μήκος
 .
.Άρα το πυθαγόρειο θεώρημα π.χ. στο τρίγωνο
 δίνει
δίνει  .
.Επομένως το εμβαδόν του ορθογωνίου είναι
 όπως θέλαμε.
όπως θέλαμε.Προφανώς ισχύει
 αφού αναφερόμαστε σε μήκος ευθ. τμήματος και
αφού αναφερόμαστε σε μήκος ευθ. τμήματος και  επειδή το τμήμα αυτό είναι σίγουρα μικρότερο της διαμέτρου.
επειδή το τμήμα αυτό είναι σίγουρα μικρότερο της διαμέτρου.(Δεν μπορεί να είναι ίσο με τη διάμετρο γιατί τότε το ορθογώνιο εκφυλίζεται σε ευθ. τμήμα).
Άρα το π.ο. της
 είναι το
είναι το  .
.Δ.2 Από τη γνωστή ανισότητα
 παίρνουμε
παίρνουμε  .
.Η τιμή αυτή επιτυγχάνεται όταν
 και φυσικά τότε ισχύει
και φυσικά τότε ισχύει  οπότε το σχήμα είναι τετράγωνο.
οπότε το σχήμα είναι τετράγωνο.Με παραγώγους έχει λίγες παραπάνω πράξεις αλλά με παραγώγους θα το λύσουν οι περισσότεροι.
Δ.3 Θέτουμε
 και το όριο γίνεται
και το όριο γίνεται  .
.Ισχύει
 άρα
άρα  .
.Επομένως το ζητούμενο όριο ισούται με
 .
.Δ.4 Μελετάμε την
 ως προς τη μονοτονία.Θα λύσουμε την ανίσωση
ως προς τη μονοτονία.Θα λύσουμε την ανίσωση 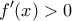 .
.Ισοδύναμα θέλουμε
 .
.Άρα στο διάστημα
 η
η  είναι γνησίως αύξουσα.Ισχύει
είναι γνησίως αύξουσα.Ισχύει  και
και ![\displaystyle{P(A),P(A-B)\in (0,1]\subset (0,5\sqrt{2})} \displaystyle{P(A),P(A-B)\in (0,1]\subset (0,5\sqrt{2})}](/forum/ext/geomar/texintegr/latexrender/pictures/45cfccdf3ce71e5dfaec80574e660814.png) .
.Επομένως

 .
.Επίσης
 και
και  .
.Η τελευταία ισχύει αφού ισχύουν και οι
 και
και  οπότε η ζητούμενη προκύπτει με πολ/σμο κατά μέλη των παραπάνω.
οπότε η ζητούμενη προκύπτει με πολ/σμο κατά μέλη των παραπάνω.Με λίγα λόγια η παράσταση
 ανήκει σίγουρα στο διάστημα
ανήκει σίγουρα στο διάστημα  ,το ίδιο και η
,το ίδιο και η  .
.Στο διάστημα αυτό όμως η
 είναι γνησίως αύξουσα άρα η
είναι γνησίως αύξουσα άρα η  δίνει τη ζητούμενη ανισότητα.
δίνει τη ζητούμενη ανισότητα.Edit:Πρόσθεσα τα πράσινα μετά από υπόδειξη του Χρ. Τσιφάκη.
τελευταία επεξεργασία από gavrilos σε Τετ Μάιος 20, 2015 11:47 am, έχει επεξεργασθεί 1 φορά συνολικά.
Γιώργος Γαβριλόπουλος
Re: Μαθηματικά Γενικής Παιδείας 2015
Ωραία λύση για το Δ4. Πάντως έχω την εντύπωση ότι οι περισσότεροι θα το λύσουν απλά αντικαθιστώντας τα ορίσματα της f στο τύπο της. Βγαίνει φυσικά, δεν έχει πάρα πολλές πράξεις (γίνονται και μερικές απλοποιήσεις) και καταλήγουμε στο  το οποίο ισχύει.
το οποίο ισχύει.
 το οποίο ισχύει.
το οποίο ισχύει.* Γιάννης Εξηνταρίδης - Μαθηματικός *
Re: Μαθηματικά Γενικής Παιδείας 2015
Το Δ3 χωρίς αλλαγή μεταβλητής είναι ο ορισμός της παραγώγου στο χ0=1.
τελευταία επεξεργασία από xr.tsif σε Τετ Μάιος 20, 2015 12:00 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Γιατί πάντα αριθμόν έχοντι. Άνευ τούτου ουδέν νοητόν και γνωστόν.
Re: Μαθηματικά Γενικής Παιδείας 2015
Στο θέμα Β
Το ότι οι πιθανότητες των ανήκουν στο σύνολο λύσεων της εξίσωσης δεν σημαίνει ότι είναι απαραίτητα και διαφορετικές μεταξύ τους.
ανήκουν στο σύνολο λύσεων της εξίσωσης δεν σημαίνει ότι είναι απαραίτητα και διαφορετικές μεταξύ τους.
Το ότι οι πιθανότητες των
 ανήκουν στο σύνολο λύσεων της εξίσωσης δεν σημαίνει ότι είναι απαραίτητα και διαφορετικές μεταξύ τους.
ανήκουν στο σύνολο λύσεων της εξίσωσης δεν σημαίνει ότι είναι απαραίτητα και διαφορετικές μεταξύ τους.Μάνος Κοθρής
Re: Μαθηματικά Γενικής Παιδείας 2015
Τα θέματα είναι δύσκολα για ένα μαθημα γενικής παιδείας.Σε σχέση με τα περσινά νομίζω πολύ πιο δύσκολα. θα ήθελα να ακούσω απόψεις συναδέλφων
Re: Μαθηματικά Γενικής Παιδείας 2015
Δόθηκε σχετική διευκρίνιση για το ερώτημα αυτό. Αν και δεν γνωρίζω ακριβώς την διευκρίνισηmanos66 έγραψε:Στο θέμα Β
Το ότι οι πιθανότητες τωνανήκουν στο σύνολο λύσεων της εξίσωσης δεν σημαίνει ότι είναι απαραίτητα και διαφορετικές μεταξύ τους.
-
AGkesk1506
- Δημοσιεύσεις: 3
- Εγγραφή: Τετ Μάιος 20, 2015 11:36 am
Re: Μαθηματικά Γενικής Παιδείας 2015
ΚΑΛΗΜΕΡΑ
Θεωρώ τα θέματα δύσκολα ΜΟΝΟ οι μαθητές κατεύθυνσης θα γράψουν
Επίσης το ΘΕΜΑ Β θέλει επεξήγηση
Θεωρώ τα θέματα δύσκολα ΜΟΝΟ οι μαθητές κατεύθυνσης θα γράψουν
Επίσης το ΘΕΜΑ Β θέλει επεξήγηση
Re: Μαθηματικά Γενικής Παιδείας 2015
Θέμα Β.
Β.1 Γνωρίζουμε κλασσικά ότι![\displaystyle{P(A),P(A\cup B),P(A\cap B),P(\Gamma)\in [0,1]} \displaystyle{P(A),P(A\cup B),P(A\cap B),P(\Gamma)\in [0,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/f219f4cdc8877b9d0438a069f1f540da.png) οπότε απορρίπτουμε όσες ρίζες δεν ανήκουν σε αυτό το διάστημα.
οπότε απορρίπτουμε όσες ρίζες δεν ανήκουν σε αυτό το διάστημα.
Επίσης (δεν γνωρίζω αν αυτή θέλει απόδειξη στις εξετάσεις).
(δεν γνωρίζω αν αυτή θέλει απόδειξη στις εξετάσεις).
Η πρώτη εξίσωση γράφεται![\displaystyle{(3x-1)(8x^2-4x-2x+1)=0\Leftrightarrow (3x-1)[4x(2x-1)-(2x-1)]=0\Leftrightarrow (3x-1)(2x-1)(4x-1)=0} \displaystyle{(3x-1)(8x^2-4x-2x+1)=0\Leftrightarrow (3x-1)[4x(2x-1)-(2x-1)]=0\Leftrightarrow (3x-1)(2x-1)(4x-1)=0}](/forum/ext/geomar/texintegr/latexrender/pictures/9f06efe99bb21f003272d5c6ceea4a72.png)
άρα ρίζες οι .Άρα αφού
.Άρα αφού  ισχύει τελικά
ισχύει τελικά  .
.
Β.2 Ισχύει .Επίσης
.Επίσης  άρα
άρα  .
.
Επίσης .Η πιθανότητα
.Η πιθανότητα  είναι η πιθανότητα να μην πραγματοποιηθεί κανένα εκ'των
είναι η πιθανότητα να μην πραγματοποιηθεί κανένα εκ'των  .
.
Δηλαδή .Επομένως
.Επομένως  .
.
Ισχύει (το μόνο που θέλουμε είναι να μην πραγματοποιούνται ταυτόχρονα).
(το μόνο που θέλουμε είναι να μην πραγματοποιούνται ταυτόχρονα).
Β.3 Ισχύει
 .
.
Β.4 Η δεύτερη εξίσωση της εκφώνησης έχει άρα
άρα  .
.
Απορρίπτοντας την αρνητική ρίζα,μένει ότι .
.
Αν τότε
τότε  άτοπο.
άτοπο.
Β.1 Γνωρίζουμε κλασσικά ότι
![\displaystyle{P(A),P(A\cup B),P(A\cap B),P(\Gamma)\in [0,1]} \displaystyle{P(A),P(A\cup B),P(A\cap B),P(\Gamma)\in [0,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/f219f4cdc8877b9d0438a069f1f540da.png) οπότε απορρίπτουμε όσες ρίζες δεν ανήκουν σε αυτό το διάστημα.
οπότε απορρίπτουμε όσες ρίζες δεν ανήκουν σε αυτό το διάστημα.Επίσης
 (δεν γνωρίζω αν αυτή θέλει απόδειξη στις εξετάσεις).
(δεν γνωρίζω αν αυτή θέλει απόδειξη στις εξετάσεις).Η πρώτη εξίσωση γράφεται
![\displaystyle{(3x-1)(8x^2-4x-2x+1)=0\Leftrightarrow (3x-1)[4x(2x-1)-(2x-1)]=0\Leftrightarrow (3x-1)(2x-1)(4x-1)=0} \displaystyle{(3x-1)(8x^2-4x-2x+1)=0\Leftrightarrow (3x-1)[4x(2x-1)-(2x-1)]=0\Leftrightarrow (3x-1)(2x-1)(4x-1)=0}](/forum/ext/geomar/texintegr/latexrender/pictures/9f06efe99bb21f003272d5c6ceea4a72.png)
άρα ρίζες οι
 .Άρα αφού
.Άρα αφού  ισχύει τελικά
ισχύει τελικά  .
.Β.2 Ισχύει
 .Επίσης
.Επίσης  άρα
άρα  .
.Επίσης
 .Η πιθανότητα
.Η πιθανότητα  είναι η πιθανότητα να μην πραγματοποιηθεί κανένα εκ'των
είναι η πιθανότητα να μην πραγματοποιηθεί κανένα εκ'των  .
.Δηλαδή
 .Επομένως
.Επομένως  .
.Ισχύει
 (το μόνο που θέλουμε είναι να μην πραγματοποιούνται ταυτόχρονα).
(το μόνο που θέλουμε είναι να μην πραγματοποιούνται ταυτόχρονα).Β.3 Ισχύει

 .
.Β.4 Η δεύτερη εξίσωση της εκφώνησης έχει
 άρα
άρα  .
.Απορρίπτοντας την αρνητική ρίζα,μένει ότι
 .
.Αν
 τότε
τότε  άτοπο.
άτοπο.Γιώργος Γαβριλόπουλος
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5284
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Μαθηματικά Γενικής Παιδείας 2015
Για το θέμα Δ.
Δ1. Φέρνουμε τη , η οποία είναι διάμετρος, αφού η γωνία
, η οποία είναι διάμετρος, αφού η γωνία  είναι ορθή.
είναι ορθή.
Στο ορθογώνιο τρίγωνο από Πυθαγόρειο Θεώρημα είναι
από Πυθαγόρειο Θεώρημα είναι  , οπότε το εμβαδό του ορθογωνίου
, οπότε το εμβαδό του ορθογωνίου  ισούται με
ισούται με  , άρα δίνεται από τη συνάρτηση
, άρα δίνεται από τη συνάρτηση 
Δ2. Η συνάρτηση είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με παράγωγο:
με παράγωγο: 
Είναι γν. αύξουσα στο , γν. φθίνουσα στο
, γν. φθίνουσα στο  , άρα παρουσιάζει μέγιστο για
, άρα παρουσιάζει μέγιστο για  .
.
Τότε , δηλαδή το
, δηλαδή το  είναι τετράγωνο.
είναι τετράγωνο.
Δ3. Για είναι
είναι 
άρα

edit: Με μικρές διαφορές από τη λύση του Gavrilos, παραπάνω. Δίχως αλλαγή μεταβλητής στο όριο, αλλά με ορισμό παραγώγου, για να αποφύγουμε τις κουραστικές συζυγείς παραστάσεις.
Διόρθωσα την τιμή . Ευχαριστώ τον nikos_el.
. Ευχαριστώ τον nikos_el.
Δ1. Φέρνουμε τη
 , η οποία είναι διάμετρος, αφού η γωνία
, η οποία είναι διάμετρος, αφού η γωνία  είναι ορθή.
είναι ορθή.Στο ορθογώνιο τρίγωνο
 από Πυθαγόρειο Θεώρημα είναι
από Πυθαγόρειο Θεώρημα είναι  , οπότε το εμβαδό του ορθογωνίου
, οπότε το εμβαδό του ορθογωνίου  ισούται με
ισούται με  , άρα δίνεται από τη συνάρτηση
, άρα δίνεται από τη συνάρτηση 
Δ2. Η συνάρτηση
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με παράγωγο:
με παράγωγο: 
Είναι γν. αύξουσα στο
 , γν. φθίνουσα στο
, γν. φθίνουσα στο  , άρα παρουσιάζει μέγιστο για
, άρα παρουσιάζει μέγιστο για  .
. Τότε
 , δηλαδή το
, δηλαδή το  είναι τετράγωνο.
είναι τετράγωνο.Δ3. Για
 είναι
είναι 
άρα


edit: Με μικρές διαφορές από τη λύση του Gavrilos, παραπάνω. Δίχως αλλαγή μεταβλητής στο όριο, αλλά με ορισμό παραγώγου, για να αποφύγουμε τις κουραστικές συζυγείς παραστάσεις.
Διόρθωσα την τιμή
 . Ευχαριστώ τον nikos_el.
. Ευχαριστώ τον nikos_el.
τελευταία επεξεργασία από Γιώργος Ρίζος σε Τετ Μάιος 20, 2015 12:59 pm, έχει επεξεργασθεί 4 φορές συνολικά.
Re: Μαθηματικά Γενικής Παιδείας 2015
Προφανώς, εννοείτε πωςΓιώργος Ρίζος έγραψε:Για το θέμα Δ.
Δ2. Η συνάρτησηείναι παραγωγίσιμη στο
με παράγωγο:

Είναι γν. αύξουσα στο, γν. φθίνουσα στο
, άρα παρουσιάζει μέγιστο για
. Τότε
, δηλαδή το
είναι τετράγωνο.
 .
.The road to success is always under construction
-
Παναγιώτης Βάγιας
- Δημοσιεύσεις: 1
- Εγγραφή: Τετ Μάιος 20, 2015 11:58 am
Re: Μαθηματικά Γενικής Παιδείας 2015
οι νόμοι του de morgan (χρησιμότατοι όπως δείχνει ο gayrilos στο β2) που (?) ακριβώς διδάσκονται στο σχολικό βιβλίο ;
οι μαθητές της θεωρητικής - μάλλον - πάνε για ολική καταστροφή , όπως και οι μέτριοι της τεχνολογικής και θετικής
οι μαθητές της θεωρητικής - μάλλον - πάνε για ολική καταστροφή , όπως και οι μέτριοι της τεχνολογικής και θετικής
- ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
- Επιμελητής
- Δημοσιεύσεις: 4658
- Εγγραφή: Κυρ Μαρ 13, 2011 9:11 pm
- Τοποθεσία: Βρυξέλλες
Re: Μαθηματικά Γενικής Παιδείας 2015
Δ1. Είναι  . Με
. Με  διάμετρος του κύκλου
διάμετρος του κύκλου  , οπότε από το Πυθαγόρειο Θεώρημα στο τρίγωνο
, οπότε από το Πυθαγόρειο Θεώρημα στο τρίγωνο

 .
.
[attachment=0]σχημα 1.png[/attachment]
Δ2. Επειδή η συνάρτηση είναι παραγωγίσιμη (τύπος πολυωνυμικής) στο διάστημα
είναι παραγωγίσιμη (τύπος πολυωνυμικής) στο διάστημα  με
με  για κάθε
για κάθε  και η
και η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  προκύπτει ότι η
προκύπτει ότι η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  και με την συνάρτηση
και με την συνάρτηση  παραγωγίσιμη (τύπος ταυτοτικής) στο
παραγωγίσιμη (τύπος ταυτοτικής) στο  προκύπτει ότι η
προκύπτει ότι η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με




Είναι

Για

και επομένως η αφού είναι συνεχής στο διάστημα
αφού είναι συνεχής στο διάστημα ![\left( {0,5\sqrt 2 } \right] \left( {0,5\sqrt 2 } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/651090273b7299e82f7d4cd3bc96b9be.png) θα είναι γνησίως αύξουσα σε αυτό.
θα είναι γνησίως αύξουσα σε αυτό.
Ομοίως για

και επομένως η (αφού είναι και συνεχής στο
(αφού είναι και συνεχής στο  ) θα είναι γνησίως φθίνουσα σε αυτό.
) θα είναι γνησίως φθίνουσα σε αυτό.
Από τα παραπάνω προκύπτει ότι η παρουσιάζει ολικό μέγιστο για
παρουσιάζει ολικό μέγιστο για  για το οποίο είναι
για το οποίο είναι
 και συνεπώς το
και συνεπώς το  είναι τετράγωνο.
είναι τετράγωνο.
Δ3. Δ3. Είναι
 .
.
Δ.4. Είναι






![\mathop \Rightarrow \limits^{f\,\gamma \nu \eta \sigma \iota \omega \varsigma \,\,\alpha \upsilon \xi o\upsilon \sigma \alpha \,\,\sigma \tau o\,\,\left( {0,5\sqrt 2 } \right]} \boxed{f\left( {\dfrac{{P\left( {A - B} \right)}}{{\sqrt {100 - {P^2}\left( {A - B} \right)} }}} \right) \leqslant f\left( {\dfrac{{P\left( A \right)}}{{\sqrt {100 - {P^2}\left( A \right)} }}} \right)} \mathop \Rightarrow \limits^{f\,\gamma \nu \eta \sigma \iota \omega \varsigma \,\,\alpha \upsilon \xi o\upsilon \sigma \alpha \,\,\sigma \tau o\,\,\left( {0,5\sqrt 2 } \right]} \boxed{f\left( {\dfrac{{P\left( {A - B} \right)}}{{\sqrt {100 - {P^2}\left( {A - B} \right)} }}} \right) \leqslant f\left( {\dfrac{{P\left( A \right)}}{{\sqrt {100 - {P^2}\left( A \right)} }}} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/22bd1866360ddadb289ebf55f3b24c64.png)
Στάθης
Υ.Σ. Στο θέμα Δ4 έχει αποδειχθεί διαφορετική ανισότητα από τη ζητούμενη Έγινε και διόρθωση στο Δ3 για να συμφωνεί με το πνεύμα του σχολικού βιβλίου
Έγινε και διόρθωση στο Δ3 για να συμφωνεί με το πνεύμα του σχολικού βιβλίου
 . Με
. Με  διάμετρος του κύκλου
διάμετρος του κύκλου  , οπότε από το Πυθαγόρειο Θεώρημα στο τρίγωνο
, οπότε από το Πυθαγόρειο Θεώρημα στο τρίγωνο
 .
.[attachment=0]σχημα 1.png[/attachment]
Δ2. Επειδή η συνάρτηση
 είναι παραγωγίσιμη (τύπος πολυωνυμικής) στο διάστημα
είναι παραγωγίσιμη (τύπος πολυωνυμικής) στο διάστημα  με
με  για κάθε
για κάθε  και η
και η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  προκύπτει ότι η
προκύπτει ότι η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  και με την συνάρτηση
και με την συνάρτηση  παραγωγίσιμη (τύπος ταυτοτικής) στο
παραγωγίσιμη (τύπος ταυτοτικής) στο  προκύπτει ότι η
προκύπτει ότι η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με 



Είναι


Για


και επομένως η
 αφού είναι συνεχής στο διάστημα
αφού είναι συνεχής στο διάστημα ![\left( {0,5\sqrt 2 } \right] \left( {0,5\sqrt 2 } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/651090273b7299e82f7d4cd3bc96b9be.png) θα είναι γνησίως αύξουσα σε αυτό.
θα είναι γνησίως αύξουσα σε αυτό. Ομοίως για


και επομένως η
 (αφού είναι και συνεχής στο
(αφού είναι και συνεχής στο  ) θα είναι γνησίως φθίνουσα σε αυτό.
) θα είναι γνησίως φθίνουσα σε αυτό.Από τα παραπάνω προκύπτει ότι η
 παρουσιάζει ολικό μέγιστο για
παρουσιάζει ολικό μέγιστο για  για το οποίο είναι
για το οποίο είναι  και συνεπώς το
και συνεπώς το  είναι τετράγωνο.
είναι τετράγωνο.Δ3. Δ3. Είναι

 .
.Δ.4. Είναι







![\mathop \Rightarrow \limits^{f\,\gamma \nu \eta \sigma \iota \omega \varsigma \,\,\alpha \upsilon \xi o\upsilon \sigma \alpha \,\,\sigma \tau o\,\,\left( {0,5\sqrt 2 } \right]} \boxed{f\left( {\dfrac{{P\left( {A - B} \right)}}{{\sqrt {100 - {P^2}\left( {A - B} \right)} }}} \right) \leqslant f\left( {\dfrac{{P\left( A \right)}}{{\sqrt {100 - {P^2}\left( A \right)} }}} \right)} \mathop \Rightarrow \limits^{f\,\gamma \nu \eta \sigma \iota \omega \varsigma \,\,\alpha \upsilon \xi o\upsilon \sigma \alpha \,\,\sigma \tau o\,\,\left( {0,5\sqrt 2 } \right]} \boxed{f\left( {\dfrac{{P\left( {A - B} \right)}}{{\sqrt {100 - {P^2}\left( {A - B} \right)} }}} \right) \leqslant f\left( {\dfrac{{P\left( A \right)}}{{\sqrt {100 - {P^2}\left( A \right)} }}} \right)}](/forum/ext/geomar/texintegr/latexrender/pictures/22bd1866360ddadb289ebf55f3b24c64.png)
Στάθης
Υ.Σ. Στο θέμα Δ4 έχει αποδειχθεί διαφορετική ανισότητα από τη ζητούμενη
- Συνημμένα
-
- σχημα 1.png (16.63 KiB) Προβλήθηκε 6721 φορές
τελευταία επεξεργασία από ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ σε Τετ Μάιος 20, 2015 3:13 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Τι περιμένετε λοιπόν ναρθεί , ποιόν καρτεράτε να σας σώσει.
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Μαθηματικά Γενικής Παιδείας 2015
Θέμα Β
Β1) ή
ή  ή
ή  ή
ή 
Άρα οι λύσεις της εξίσωσης είναι οι αριθμοί με
με 
Όμως άρα
άρα  κι έτσι
κι έτσι 



που οκοκληρώνει την απόδειξη του ερωτήματος.
Β2)
Για τον υπολογισμό του θα κάνουμε το εξής: Από το σχήμα του Venn με ενδεχόμενα τα
θα κάνουμε το εξής: Από το σχήμα του Venn με ενδεχόμενα τα  παρατηρούμε ότι
παρατηρούμε ότι  άρα
άρα 
Έτσι
Επίσης κι έτσι
κι έτσι 
Β3) Είναι
Επειδή άρα με αντικατάσταση έχουμε
άρα με αντικατάσταση έχουμε  .
.
Επειδή τα ενδεχόμενα και
και  είναι ασυμβίβαστα άρα από τον απλό προσθετικό νόμο έχουμε:
είναι ασυμβίβαστα άρα από τον απλό προσθετικό νόμο έχουμε:

Β4) ή
ή 
Όμως άρα
άρα 
Αν τα ήταν ασυμβίβαστα τότε από τον απλό προσθετικό νόμο θα είχαμε
ήταν ασυμβίβαστα τότε από τον απλό προσθετικό νόμο θα είχαμε  , άτοπο διότι
, άτοπο διότι  . Άρα τα
. Άρα τα  δεν είναι ασυμβίβαστα.
δεν είναι ασυμβίβαστα.
 Προφανώς οι θεματοδότες εννοούσαν ότι οι πιθανότητες
Προφανώς οι θεματοδότες εννοούσαν ότι οι πιθανότητες  είναι διαφορετικές μεταξύ τους ανά δύο.
είναι διαφορετικές μεταξύ τους ανά δύο.
Αλέξανδρος
Β1)
 ή
ή  ή
ή  ή
ή 
Άρα οι λύσεις της εξίσωσης είναι οι αριθμοί
 με
με 
Όμως
 άρα
άρα  κι έτσι
κι έτσι 



που οκοκληρώνει την απόδειξη του ερωτήματος.
Β2)

Για τον υπολογισμό του
 θα κάνουμε το εξής: Από το σχήμα του Venn με ενδεχόμενα τα
θα κάνουμε το εξής: Από το σχήμα του Venn με ενδεχόμενα τα  παρατηρούμε ότι
παρατηρούμε ότι  άρα
άρα 
Έτσι

Επίσης
 κι έτσι
κι έτσι 
Β3) Είναι

Επειδή
 άρα με αντικατάσταση έχουμε
άρα με αντικατάσταση έχουμε  .
.Επειδή τα ενδεχόμενα
 και
και  είναι ασυμβίβαστα άρα από τον απλό προσθετικό νόμο έχουμε:
είναι ασυμβίβαστα άρα από τον απλό προσθετικό νόμο έχουμε: 
Β4)
 ή
ή 
Όμως
 άρα
άρα 
Αν τα
 ήταν ασυμβίβαστα τότε από τον απλό προσθετικό νόμο θα είχαμε
ήταν ασυμβίβαστα τότε από τον απλό προσθετικό νόμο θα είχαμε  , άτοπο διότι
, άτοπο διότι  . Άρα τα
. Άρα τα  δεν είναι ασυμβίβαστα.
δεν είναι ασυμβίβαστα. Προφανώς οι θεματοδότες εννοούσαν ότι οι πιθανότητες
Προφανώς οι θεματοδότες εννοούσαν ότι οι πιθανότητες  είναι διαφορετικές μεταξύ τους ανά δύο.
είναι διαφορετικές μεταξύ τους ανά δύο.Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
stranton
- Επιμελητής
- Δημοσιεύσεις: 679
- Εγγραφή: Πέμ Ιουν 25, 2009 5:00 pm
- Τοποθεσία: Σπάρτη
- Επικοινωνία:
Re: Μαθηματικά Γενικής Παιδείας 2015
ΘΕΜΑ Γ
Γ1
Το ποσοστό των παρατηρήσεων του δείγματος που είναι μικρότερες του 10 είναι 10%, άρα .
.
Το ποσοστό των παρατηρήσεων του δείγματος που είναι μεγαλύτερες ή ίσες του 16 είναι 30%, άρα .
.
Στο κυκλικό διάγραμμα σχετικών συχνοτήτων, η γωνία του κυκλικού τομέα που αντιστοιχεί στην 3η κλάση είναι ,
,
άρα , δηλαδή
, δηλαδή  .
.
Έχουμε ότι .
.
Τα κέντρα των κλάσεων είναι: .
.
Επομένως,




και
Επομένως, και
και  .
.
Γ2
Η διασπορά είναι:

 .
.
Η τυπική απόκλιση είναι: .
.
Ο συντελεστής μεταβολής είναι: .
.
Άρα το δείγμα των παρατηρήσεων δεν είναι ομοιογενές.
Γ3
Είναι


 .
.
Γ4
Για είναι
είναι 
Έστω οι παρατηρήσεις
οι παρατηρήσεις  και
και  .
.
Τότε και
και  .
.
Άρα
και .
.
Γ1
Το ποσοστό των παρατηρήσεων του δείγματος που είναι μικρότερες του 10 είναι 10%, άρα
 .
.Το ποσοστό των παρατηρήσεων του δείγματος που είναι μεγαλύτερες ή ίσες του 16 είναι 30%, άρα
 .
.Στο κυκλικό διάγραμμα σχετικών συχνοτήτων, η γωνία του κυκλικού τομέα που αντιστοιχεί στην 3η κλάση είναι
 ,
, άρα
 , δηλαδή
, δηλαδή  .
.Έχουμε ότι
 .
.Τα κέντρα των κλάσεων είναι:
 .
.Επομένως,





και

Επομένως,
 και
και  .
.Γ2
Η διασπορά είναι:


 .
.Η τυπική απόκλιση είναι:
 .
. Ο συντελεστής μεταβολής είναι:
 .
.Άρα το δείγμα των παρατηρήσεων δεν είναι ομοιογενές.
Γ3
Είναι



 .
.Γ4
Για
 είναι
είναι 
Έστω
 οι παρατηρήσεις
οι παρατηρήσεις  και
και  .
.Τότε
 και
και  .
.Άρα

και
 .
.
τελευταία επεξεργασία από stranton σε Τετ Μάιος 20, 2015 12:38 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Στράτης Αντωνέας
-
ΚΟΥΤΣΟΥΚΟΣ ΓΙΑΝΝΗΣ
- Δημοσιεύσεις: 148
- Εγγραφή: Πέμ Ιουν 03, 2010 2:43 pm
Re: Μαθηματικά Γενικής Παιδείας 2015
Θεωρώ οτι τα φετινά θέματα είναι πιο δύσκολα σε σχέση με τα περσινά.
Έχουν προσεγγίσεις μέσα απο ασκήσεις , ερωτήσεις του σχολικού βιβλίου.
Λογικά στο Β1 θα πρέπει να τους έστειλαν διευκρίνιση οτι οι πιθανότητες των ενδεχομένων είναι διαφορετικές μεταξύ τους.
είναι διαφορετικές μεταξύ τους.
Επίσης στο Γ2 θα πρέπει ο εξεταζόμενος να γνωρίζει και να έχει δουλέψει οτι .
.
Επίσης με λιγη προσοχη στο Δ3 βγαίνει ευκολα ο τύπος της παραγώγου. Στο Δ4 πιστεύω οτι προσεγγιζεται πιο ευκολα απο παιδια της κατευθυνσης και οχι της θεωρητικής.
Κατα την άποψή μου τα θέματα είναι πιο ποιοτικά σε σχέση με τις προηγούμενες χρονιές και χωρίς τον χαμό των πράξεων.
Έχουν προσεγγίσεις μέσα απο ασκήσεις , ερωτήσεις του σχολικού βιβλίου.
Λογικά στο Β1 θα πρέπει να τους έστειλαν διευκρίνιση οτι οι πιθανότητες των ενδεχομένων
 είναι διαφορετικές μεταξύ τους.
είναι διαφορετικές μεταξύ τους. Επίσης στο Γ2 θα πρέπει ο εξεταζόμενος να γνωρίζει και να έχει δουλέψει οτι
 .
.Επίσης με λιγη προσοχη στο Δ3 βγαίνει ευκολα ο τύπος της παραγώγου. Στο Δ4 πιστεύω οτι προσεγγιζεται πιο ευκολα απο παιδια της κατευθυνσης και οχι της θεωρητικής.
Κατα την άποψή μου τα θέματα είναι πιο ποιοτικά σε σχέση με τις προηγούμενες χρονιές και χωρίς τον χαμό των πράξεων.
Re: Μαθηματικά Γενικής Παιδείας 2015
Γνωρίζει κάποιος με ακρίβεια το περιεχόμενο της διευκρίνησης;;
Νῆφε καί μέμνασο ἀπιστεῖν˙ ἄρθρα ταῦτα γάρ φρενῶν
Νοῦς ὁρᾷ καί Νοῦς ἀκούει˙ τἆλλα κωφά καί τυφλά.
...
Νοῦς ὁρᾷ καί Νοῦς ἀκούει˙ τἆλλα κωφά καί τυφλά.
...
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες

 , σύμφωνα με τη σχέση
, σύμφωνα με τη σχέση  γράφεται ως
γράφεται ως 