Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5283
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Αναρτήθηκαν τα θέματα των σημερινών επαναληπτικών εξετάσεων και των ομογενών.
- Συνημμένα
-
- ΜΑΘΗΜΑΤΙΚΑ_ΟΜΟΓ_2021_-6.pdf
- (187.66 KiB) Μεταφορτώθηκε 150 φορές
-
- Ε01 ΜΑΘΗΜΑΤΙΚΑ_ΕΠΑΝΑΛ_2021_NEO-9.pdf
- (205.87 KiB) Μεταφορτώθηκε 246 φορές
Λέξεις Κλειδιά:
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5283
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Με την πρώτη ματιά η προσοχή μου έπεσε το θέμα Γ. Ομολογώ ότι μού κέντρισε το ενδιαφέρον και μού άρεσε!
Γ1
Για![\displaystyle \theta \in \left[ {0,\;\pi } \right] \displaystyle \theta \in \left[ {0,\;\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/7afa5a4f0963b26ad423a921d664cb73.png) είναι
είναι 

οπότε , αφού το συνημίτονο είναι μη αρνητικό στο 1ο τεταρτημόριο).
, αφού το συνημίτονο είναι μη αρνητικό στο 1ο τεταρτημόριο).
Επίσης , οπότε, εφόσον έχουμε κινήσεις με σταθερές ταχύτητες, είναι
, οπότε, εφόσον έχουμε κινήσεις με σταθερές ταχύτητες, είναι ![\displaystyle t\left( \theta \right) = \frac{{{\rm A}\Gamma }}{{{v_1}}} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{{{v_2}}} = \frac{{{\rm A}\Gamma }}{2} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{4} = \sigma \upsilon \nu \frac{\theta }{2} + \frac{\theta }{4},\;\;\theta \in \left[ {0,\pi } \right] \displaystyle t\left( \theta \right) = \frac{{{\rm A}\Gamma }}{{{v_1}}} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{{{v_2}}} = \frac{{{\rm A}\Gamma }}{2} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{4} = \sigma \upsilon \nu \frac{\theta }{2} + \frac{\theta }{4},\;\;\theta \in \left[ {0,\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/4ead19118f5f3ed3a0ffa3f33e559e19.png)
Γ2
Η συνάρτηση είναι παραγωγίσιμη με
Είναι
Για είναι
είναι  και για
και για ![\displaystyle \theta \in \left( {\frac{\pi }{3},\;\pi } \right] \displaystyle \theta \in \left( {\frac{\pi }{3},\;\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/323b9f6a5a748186bd84164558e4d68b.png) είναι
είναι  , οπότε η συνάρτηση παρουσιάζει μέγιστο στο
, οπότε η συνάρτηση παρουσιάζει μέγιστο στο 
(Δεν ζητείται εδώ, αλλά χρειάζεται παρακάτω: με τιμή )
)
Γ3
Για κωπηλατεί ευθύγραμμα διαδρομή
κωπηλατεί ευθύγραμμα διαδρομή  σε χρόνο
σε χρόνο 
(Πράγματι, )
)
Για , πάει περπατώντας στην ημιπεριφέρεια μήκους
, πάει περπατώντας στην ημιπεριφέρεια μήκους  σε χρόνο
σε χρόνο  .
.
(Είναι ).
).
Στο![\displaystyle \left[ {0,\;\frac{\pi }{3}} \right] \displaystyle \left[ {0,\;\frac{\pi }{3}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/28c4e45f81ba36ef240b2924f5752fd2.png) η συνάρτηση είναι γν. αύξουσα κι έχει Π.Τ.
η συνάρτηση είναι γν. αύξουσα κι έχει Π.Τ. ![\displaystyle \left[ {1,\;\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2}} \right] \displaystyle \left[ {1,\;\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/e38a535dd5ff7ebc5f904d6d74ec1212.png) , ενώ στο
, ενώ στο ![\displaystyle \left[ {\frac{\pi }{3},\;\pi } \right] \displaystyle \left[ {\frac{\pi }{3},\;\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/38b14facf673da4a7909eaa576398727.png) έχει είναι γν. φθίνουσα κι έχει Π.Τ.
έχει είναι γν. φθίνουσα κι έχει Π.Τ. ![\displaystyle \left[ {\frac{\pi }{4},\;\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2}} \right] \displaystyle \left[ {\frac{\pi }{4},\;\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/68f450e39210c7a5724bb3bcb1a3f4a8.png) , άρα η ελάχιστη διαδρομή είναι η III, αφού
, άρα η ελάχιστη διαδρομή είναι η III, αφού  .
.
edit: Στο Γ1 εννοείται ότι ο υπολογισμός του μήκους του μπορεί να γίνει και δίχως τη χρήση του Ν. Συνημιτόνων και του τύπου διπλασίου τόξου, φέρνοντας την κάθετη από το
μπορεί να γίνει και δίχως τη χρήση του Ν. Συνημιτόνων και του τύπου διπλασίου τόξου, φέρνοντας την κάθετη από το  στην
στην  . Οπότε
. Οπότε  κ.ο.κ. Απλά ήθελα να αποφύγω την κατασκευή σχήματος στην αρχική ανάρτηση.
κ.ο.κ. Απλά ήθελα να αποφύγω την κατασκευή σχήματος στην αρχική ανάρτηση.
Πρόσθεσα τη φράση με τα πράσινα γράμματα στο Γ1, μετά την υπόδειξη του Χρήστου (δείτε παρακάτω #9), ώστε να δικαιολογείται ο τύπος που δίνει το χρόνο ως πηλίκο διανυθέντος διαστήματος προς την ταχύτητα.
Γ1
Για
![\displaystyle \theta \in \left[ {0,\;\pi } \right] \displaystyle \theta \in \left[ {0,\;\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/7afa5a4f0963b26ad423a921d664cb73.png) είναι
είναι 

οπότε
 , αφού το συνημίτονο είναι μη αρνητικό στο 1ο τεταρτημόριο).
, αφού το συνημίτονο είναι μη αρνητικό στο 1ο τεταρτημόριο).Επίσης
 , οπότε, εφόσον έχουμε κινήσεις με σταθερές ταχύτητες, είναι
, οπότε, εφόσον έχουμε κινήσεις με σταθερές ταχύτητες, είναι ![\displaystyle t\left( \theta \right) = \frac{{{\rm A}\Gamma }}{{{v_1}}} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{{{v_2}}} = \frac{{{\rm A}\Gamma }}{2} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{4} = \sigma \upsilon \nu \frac{\theta }{2} + \frac{\theta }{4},\;\;\theta \in \left[ {0,\pi } \right] \displaystyle t\left( \theta \right) = \frac{{{\rm A}\Gamma }}{{{v_1}}} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{{{v_2}}} = \frac{{{\rm A}\Gamma }}{2} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{4} = \sigma \upsilon \nu \frac{\theta }{2} + \frac{\theta }{4},\;\;\theta \in \left[ {0,\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/4ead19118f5f3ed3a0ffa3f33e559e19.png)
Γ2
Η συνάρτηση είναι παραγωγίσιμη με

Είναι

Για
 είναι
είναι  και για
και για ![\displaystyle \theta \in \left( {\frac{\pi }{3},\;\pi } \right] \displaystyle \theta \in \left( {\frac{\pi }{3},\;\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/323b9f6a5a748186bd84164558e4d68b.png) είναι
είναι  , οπότε η συνάρτηση παρουσιάζει μέγιστο στο
, οπότε η συνάρτηση παρουσιάζει μέγιστο στο 
(Δεν ζητείται εδώ, αλλά χρειάζεται παρακάτω: με τιμή
 )
)Γ3
Για
 κωπηλατεί ευθύγραμμα διαδρομή
κωπηλατεί ευθύγραμμα διαδρομή  σε χρόνο
σε χρόνο 
(Πράγματι,
 )
)Για
 , πάει περπατώντας στην ημιπεριφέρεια μήκους
, πάει περπατώντας στην ημιπεριφέρεια μήκους  σε χρόνο
σε χρόνο  .
.(Είναι
 ).
).Στο
![\displaystyle \left[ {0,\;\frac{\pi }{3}} \right] \displaystyle \left[ {0,\;\frac{\pi }{3}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/28c4e45f81ba36ef240b2924f5752fd2.png) η συνάρτηση είναι γν. αύξουσα κι έχει Π.Τ.
η συνάρτηση είναι γν. αύξουσα κι έχει Π.Τ. ![\displaystyle \left[ {1,\;\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2}} \right] \displaystyle \left[ {1,\;\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/e38a535dd5ff7ebc5f904d6d74ec1212.png) , ενώ στο
, ενώ στο ![\displaystyle \left[ {\frac{\pi }{3},\;\pi } \right] \displaystyle \left[ {\frac{\pi }{3},\;\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/38b14facf673da4a7909eaa576398727.png) έχει είναι γν. φθίνουσα κι έχει Π.Τ.
έχει είναι γν. φθίνουσα κι έχει Π.Τ. ![\displaystyle \left[ {\frac{\pi }{4},\;\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2}} \right] \displaystyle \left[ {\frac{\pi }{4},\;\frac{\pi }{{12}} + \frac{{\sqrt 3 }}{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/68f450e39210c7a5724bb3bcb1a3f4a8.png) , άρα η ελάχιστη διαδρομή είναι η III, αφού
, άρα η ελάχιστη διαδρομή είναι η III, αφού  .
.edit: Στο Γ1 εννοείται ότι ο υπολογισμός του μήκους του
 μπορεί να γίνει και δίχως τη χρήση του Ν. Συνημιτόνων και του τύπου διπλασίου τόξου, φέρνοντας την κάθετη από το
μπορεί να γίνει και δίχως τη χρήση του Ν. Συνημιτόνων και του τύπου διπλασίου τόξου, φέρνοντας την κάθετη από το  στην
στην  . Οπότε
. Οπότε  κ.ο.κ. Απλά ήθελα να αποφύγω την κατασκευή σχήματος στην αρχική ανάρτηση.
κ.ο.κ. Απλά ήθελα να αποφύγω την κατασκευή σχήματος στην αρχική ανάρτηση.Πρόσθεσα τη φράση με τα πράσινα γράμματα στο Γ1, μετά την υπόδειξη του Χρήστου (δείτε παρακάτω #9), ώστε να δικαιολογείται ο τύπος που δίνει το χρόνο ως πηλίκο διανυθέντος διαστήματος προς την ταχύτητα.
τελευταία επεξεργασία από Γιώργος Ρίζος σε Κυρ Σεπ 12, 2021 7:14 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- exdx
- Επιμελητής
- Δημοσιεύσεις: 1739
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Είναι το πρόβλημα "ο οικολόγος Ed" του Μ Spivak . Θα υπάρχει κι αλλού .Γιώργος Ρίζος έγραψε: ↑Τετ Σεπ 08, 2021 6:52 pmΜε την πρώτη ματιά η προσοχή μου έπεσε το θέμα Γ. Ομολογώ ότι μού κέντρισε το ενδιαφέρον και μού άρεσε!
Kαλαθάκης Γιώργης
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Πολύ ωραίο θέμα πράγματι !Γιώργος Ρίζος έγραψε: ↑Τετ Σεπ 08, 2021 6:52 pmedit: Στο Γ1 εννοείται ότι ο υπολογισμός του μήκους τουμπορεί να γίνει και δίχως τη χρήση του Ν. Συνημιτόνων και του τύπου διπλασίου τόξου, φέρνοντας την κάθετη από το
στην
. Οπότε
κ.ο.κ. Απλά ήθελα να αποφύγω την κατασκευή σχήματος στην αρχική ανάρτηση.
Επιτρέψτε μου, Μια ακόμη εναλλακτική προσεγγιση για το συγκεκριμένο:
Η
 οπότε με νόμο των ημιτόνων στο
οπότε με νόμο των ημιτόνων στο  προκύπτει το ζητούμενο για την
προκύπτει το ζητούμενο για την 
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Επιτρέψτε μου να θεωρήσω το Γ1 αρκετα δύσκολο τη στιγμη που χρειάζονται τύποι που οι οδηγίες ορίζουν να διδαχθούν σε 1 διδακτική ώρα εκτός και με άλλη λυση δεν χρειαζεται το 3.7 της αλγεβρας της Β Λυκείου ή τον νομο των ημιτόνων που νομίζω ότι είναι εκτός ύλης. (Αν ήταν θεμα Ιουνιου θα υπήρχε τεραστια αποτυχία)
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5283
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Αγαπητέ prof καλώς ήλθες στοprof έγραψε: ↑Πέμ Σεπ 09, 2021 1:30 pmΕπιτρέψτε μου να θεωρήσω το Γ1 αρκετα δύσκολο τη στιγμη που χρειάζονται τύποι που οι οδηγίες ορίζουν να διδαχθούν σε 1 διδακτική ώρα εκτός και με άλλη λυση δεν χρειαζεται το 3.7 της αλγεβρας της Β Λυκείου ή τον νομο των ημιτόνων που νομίζω ότι είναι εκτός ύλης. (Αν ήταν θεμα Ιουνιου θα υπήρχε τεραστια αποτυχία)
Επέλεξα να δώσω τη λύση με Ν. Συνημιτόνων, που προσωπικά τον θεωρώ σημαντικότατο εργαλείο στην επίλυση τέτοιων προβλημάτων, δίχως να υποτιμώ τις πιο απλές προσεγγίσεις:
Ο μαθητής πρέπει να ξέρει:
Σχέση επίκεντρης - εγγεγραμμένης που βαίνουν στο ίδιο τόξο.
Το ύψος στη βάση ισοσκελούς ταυτίζεται με τη διάμεσό του
Ορισμό συνημιτόνου σε ορθογώνιο τρίγωνο
"Τα ξέρω" σημαίνει ότι "μπορώ να τα συνδυάζω" σε ένα όμορφο πρόβλημα όπως το παραπάνω.
Αν δεν τα ξέρει αυτά ή δεν μπορεί να τα εφαρμόσει, δεν βλέπω πώς θα μπορέσει να κατανοήσει τα ανώτερα μαθηματικά που απαιτεί ή όποια σχολή πετύχει κι ας έχει μάθει απέξω δεκάδες τεχνικές και συνταγές ασκήσεων με υπαρξιακά ερωτήματα που όμως είναι ανύπαρκτα στη φύση και στα ουσιώδη μαθηματικά.
Δίνω τη λύση με τα παραπάνω εργαλεία.
Γ1
 ως εγγεγραμμένη που βαίνει στο ίδιο τόξο με την επίκεντρη
ως εγγεγραμμένη που βαίνει στο ίδιο τόξο με την επίκεντρη  .
. ισοσκελές με
ισοσκελές με  . Φέρνουμε την κάθετη
. Φέρνουμε την κάθετη  στην
στην  που είναι και διάμεσος.
που είναι και διάμεσος.Τότε
 .
.Επίσης
 , οπότε
, οπότε ![\displaystyle t\left( \theta \right) = \frac{{{\rm A}\Gamma }}{2} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{4} = \sigma \upsilon \nu \frac{\theta }{2} + \frac{\theta }{4},\;\;\theta \in \left[ {0,\pi } \right] \displaystyle t\left( \theta \right) = \frac{{{\rm A}\Gamma }}{2} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{4} = \sigma \upsilon \nu \frac{\theta }{2} + \frac{\theta }{4},\;\;\theta \in \left[ {0,\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/8bfa0e5708d44c732467a5175cdb2a44.png)
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
ακόμη και αυτη η γνώση μπορεί να αντικατασταθεί από μια που διδάσκεται νωρίτερα: ηΓιώργος Ρίζος έγραψε: ↑Πέμ Σεπ 09, 2021 7:23 pm
Ο μαθητής πρέπει να ξέρει:
Σχέση επίκεντρης - εγγεγραμμένης που βαίνουν στο ίδιο τόξο.
...
 είναι εξωτερική γωνία ισοσκελούς τριγώνου
είναι εξωτερική γωνία ισοσκελούς τριγώνουRe: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Aλλη μια λυση πιο απλη θα ηταν :

Φερνοντας την καθετο η οποια λογο ισοσκελους τριγωνου θα ειναι και διαμεσος και διχοτομος, χωριζει την γωνια σε 2 ισες εστω
με


Φερνοντας την καθετο η οποια λογο ισοσκελους τριγωνου θα ειναι και διαμεσος και διχοτομος, χωριζει την γωνια σε 2 ισες εστω

με


- Christos.N
- Δημοσιεύσεις: 2105
- Εγγραφή: Πέμ Νοέμ 26, 2009 2:28 pm
- Τοποθεσία: Ίλιον
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Γιώργο όλα καλά , αλλά τόσο προφανή είναι τα πηλίκα;Γιώργος Ρίζος έγραψε: ↑Τετ Σεπ 08, 2021 6:52 pmΜε την πρώτη ματιά η προσοχή μου έπεσε το θέμα Γ. Ομολογώ ότι μού κέντρισε το ενδιαφέρον και μού άρεσε!
Γ1
...οπότε![\displaystyle t\left( \theta \right) = \frac{{{\rm A}\Gamma }}{2} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{4} = \sigma \upsilon \nu \frac{\theta }{2} + \frac{\theta }{4},\;\;\theta \in \left[ {0,\pi } \right] \displaystyle t\left( \theta \right) = \frac{{{\rm A}\Gamma }}{2} + \frac{{\mathop {{\rm B}\Gamma }\limits^ \cap }}{4} = \sigma \upsilon \nu \frac{\theta }{2} + \frac{\theta }{4},\;\;\theta \in \left[ {0,\pi } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/8bfa0e5708d44c732467a5175cdb2a44.png)
Χρήστος Ντάβας
Wir müssen wissen — wir werden wissen! D.Hilbert
Wir müssen wissen — wir werden wissen! D.Hilbert
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Αν φέρουμε την ΒΓ, τότε το ΑΓ υπολογίζεται επίσης πάρα πολύ απλά, αφού ΑΓΒ είναι τρίγωνο ορθογώνιο στο Γ, οπότε
 κ.τ.λ.π
κ.τ.λ.π
 κ.τ.λ.π
κ.τ.λ.πΚαλό Καλοκαίρι!
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Αντίθετα εμένα με ξένισε το γεγονός ότι έδωσαν τον τύπο του μήκους τόξου. Είναι αδιανόητο να θέλουν να εισαχθούν σε πολυτεχνικές ή φυσικομαθηματικές σχολές και να μην γνωρίουν στοιχειώδη τριγωνομετρία. Εξάλλου ο νόμος των συνημιτόνων χρησιμοποιείται ευρύτατα και στη Φυσική, άρα τον ξέρουν και από εκεί.prof έγραψε: ↑Πέμ Σεπ 09, 2021 1:30 pmΕπιτρέψτε μου να θεωρήσω το Γ1 αρκετα δύσκολο τη στιγμη που χρειάζονται τύποι που οι οδηγίες ορίζουν να διδαχθούν σε 1 διδακτική ώρα εκτός και με άλλη λυση δεν χρειαζεται το 3.7 της αλγεβρας της Β Λυκείου ή τον νομο των ημιτόνων που νομίζω ότι είναι εκτός ύλης. (Αν ήταν θεμα Ιουνιου θα υπήρχε τεραστια αποτυχία)
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
το θεμα αυτο υπαρχει στο βιβλίο μου "οι ασκήσεις" που εχει ανεβασει ο Ν. Μαυρογιάννης στον Εκθετη
ΜΟΥ ΕΚΑΝΕ ΕΝΤΥΠΩΣΗ γιατι είναι ιδια ΜΕΧΡΙ και τα νούμερα
Είναι στι κεφάλαιο των παραγώγων η άσκηση 9Β3
Λετε να το πήραν από εκεί η είναι ΣΚΑΝΔΑΛΩΔΗΣ ΣΥΜΠΤΩΣΗ?
ΜΟΥ ΕΚΑΝΕ ΕΝΤΥΠΩΣΗ γιατι είναι ιδια ΜΕΧΡΙ και τα νούμερα
Είναι στι κεφάλαιο των παραγώγων η άσκηση 9Β3
Λετε να το πήραν από εκεί η είναι ΣΚΑΝΔΑΛΩΔΗΣ ΣΥΜΠΤΩΣΗ?
- exdx
- Επιμελητής
- Δημοσιεύσεις: 1739
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Μάλλον είναι απλή σύμπτωση
Η πρωτότυπη απ΄τον Spivak : (Κυκλοφορεί και στο διαδίκτυο)
Ecological Ed must cross a circular lake of radius 1 mile.
He can row across at 2 mph or walk around at 4 mph, or he can row part way and walk the rest .
What route should he take so as to;
Απλά άλλαξαν τα μίλια σε χιλιόμετρα
Η πρωτότυπη απ΄τον Spivak : (Κυκλοφορεί και στο διαδίκτυο)
Ecological Ed must cross a circular lake of radius 1 mile.
He can row across at 2 mph or walk around at 4 mph, or he can row part way and walk the rest .
What route should he take so as to;
Απλά άλλαξαν τα μίλια σε χιλιόμετρα
Kαλαθάκης Γιώργης
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1290
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: Θέματα επαναληπτικών εξετάσεων Σεπτεμβρίου 2021
Στην παρούσα δημοσίευση θα δούμε το τέταρτο θέμα των Επαναληπτικών του 2021.
ΘΕΜΑ Δ
Δίνεται η συνάρτηση με τύπο
με τύπο 
και συνάρτηση με τύπο
με τύπο 
για την οποία το όριο υπάρχει στο
υπάρχει στο 
Δ1. Να αποδείξετε ότι
MONAΔΕΣ 6
Δ2. Να αποδείξετε ότι η μοναδική εφαπτομένη της γραφικής παράστασης της συνάρτησης
που διέρχεται από το σημείο είναι η ευθεία
είναι η ευθεία  (μονάδες 3)
(μονάδες 3)
Στη συνέχεια, να αποδείξετε ότι η ευθεία εφάπτεται και στη
εφάπτεται και στη
γραφική παράσταση της συνάρτησης (μονάδες 3),
(μονάδες 3),
MONAΔΕΣ 6
Δ3. Να αποδείξετε ότι για κάθε
για κάθε 
MONAΔΕΣ 6
Δ4. Να αποδείξετε ότι η εξίσωση :

έχει μία τουλάχιστον ρίζα στο διάστημα
MONAΔΕΣ 7
Δ1

![\displaystyle{ \lim_{x \rightarrow +\infty}\left (x \sqrt{ 1-\frac{a}{x} }+ax \right )={ \lim_{x \rightarrow +\infty}\left [ x \left ( \sqrt{1+\frac{a}{x}}+a \right ) \right ]=+\infty(1+a) \displaystyle{ \lim_{x \rightarrow +\infty}\left (x \sqrt{ 1-\frac{a}{x} }+ax \right )={ \lim_{x \rightarrow +\infty}\left [ x \left ( \sqrt{1+\frac{a}{x}}+a \right ) \right ]=+\infty(1+a)](/forum/ext/geomar/texintegr/latexrender/pictures/5367a9bd301066c020b8a3f33f0b6977.png)
Διακρίνω περιπτώσεις:
1.
Σε αυτήν την περίπτωση το όριο είναι ίσο με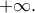
2.
Σε αυτήν την περίπτωση το όριο είναι ίσο με
3.Εξετάζω τι γίνεται για
Σε αυτήν την περίπτωση


Aναγκαστικά λοιπόν
Δ2. Η εφαπτομένη της γραφικής παράστασης της στο τυχαίο σημείο της
στο τυχαίο σημείο της 
έχει εξίσωση
H εν λόγω εφαπτομένη διέρχεται από το σημείο αν και μόνον αν
αν και μόνον αν

H εφαπτομένη της γραφικής παράστασης της στο σημείο της
στο σημείο της 
έχει εξίσωση
Θα αποδειχθεί ότι η ευθεία αυτή εφάπτεται στη γραφική παράσταση της .
.

Θα θέλαμε ένα σημείο τέτοιο ώστε
τέτοιο ώστε

H εφαπτομένη της γραφικής παράστασης της στο σημείο της
στο σημείο της 
έχει εξίσωση

Δ3. Αυτό που θέλουμε να αποδειχθεί είναι η ανισότητα
 για κάθε
για κάθε 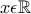
Ασφαλώς ξέρουμε ότι
με την ισότητα αν και μόνον αν .
.
Eπίσης
με την ισότητα αν και μόνον αν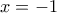 .
.
Έτσι μπορεί να γραφεί άφοβα ότι
 για κάθε
για κάθε 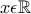
Δ4. Έστω η συνάρτηση
![H\left ( x \right )=\left ( x-k-1 \right )\left [ f\left ( x-1 \right ) -x\right ]+\left ( x-k \right )\left [ f\left ( x \right )-g\left ( x \right ) \right ] H\left ( x \right )=\left ( x-k-1 \right )\left [ f\left ( x-1 \right ) -x\right ]+\left ( x-k \right )\left [ f\left ( x \right )-g\left ( x \right ) \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/2513a12a8f208bda987120d5ee607038.png)
με![x\epsilon \left [ k,k+1 \right ] x\epsilon \left [ k,k+1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/2991aca17439ae6a92f4aa4ed1864977.png)
H είναι συνεχής στο
είναι συνεχής στο ![\left [ k,k+1 \right ] \left [ k,k+1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/ab07f3b7f823a40166b6f1d76a1da0de.png)

όπως είδαμε στο προηγούμενο σκέλος.

Γράφω αιτιολόγηση του αρνητικού προσήμου.
Eίναι βέβαιο ότι
με την ισότητα να ισχύει αν και μόνον αν .
.
H τιμή όμως αυτή έχει εξαιρεθεί από τη διατύπωση του θέματος.
Αναγκαστικά λοιπόν
Σύμφωνα με το θεώρημα Bolzano υπάρχει ένα τουλάχιστον
τέτοιο ώστε
![H\left ( \rho \right )=0\Leftrightarrow \left ( \rho -k-1 \right )\left [ f\left ( \rho -1 \right )-\rho \right ]+\left ( \rho -k \right )\left [ f\left ( \rho \right )-g\left ( \rho \right ) \right ]=0\Leftrightarrow H\left ( \rho \right )=0\Leftrightarrow \left ( \rho -k-1 \right )\left [ f\left ( \rho -1 \right )-\rho \right ]+\left ( \rho -k \right )\left [ f\left ( \rho \right )-g\left ( \rho \right ) \right ]=0\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/7b116bb2a31a328b7e433df41f7ed1b0.png)

ΘΕΜΑ Δ
Δίνεται η συνάρτηση
 με τύπο
με τύπο 
και συνάρτηση
 με τύπο
με τύπο 
για την οποία το όριο
 υπάρχει στο
υπάρχει στο 
Δ1. Να αποδείξετε ότι

MONAΔΕΣ 6
Δ2. Να αποδείξετε ότι η μοναδική εφαπτομένη της γραφικής παράστασης της συνάρτησης

που διέρχεται από το σημείο
 είναι η ευθεία
είναι η ευθεία  (μονάδες 3)
(μονάδες 3)Στη συνέχεια, να αποδείξετε ότι η ευθεία
 εφάπτεται και στη
εφάπτεται και στη γραφική παράσταση της συνάρτησης
 (μονάδες 3),
(μονάδες 3),MONAΔΕΣ 6
Δ3. Να αποδείξετε ότι
 για κάθε
για κάθε 
MONAΔΕΣ 6
Δ4. Να αποδείξετε ότι η εξίσωση :

έχει μία τουλάχιστον ρίζα στο διάστημα

MONAΔΕΣ 7
Δ1


![\displaystyle{ \lim_{x \rightarrow +\infty}\left (x \sqrt{ 1-\frac{a}{x} }+ax \right )={ \lim_{x \rightarrow +\infty}\left [ x \left ( \sqrt{1+\frac{a}{x}}+a \right ) \right ]=+\infty(1+a) \displaystyle{ \lim_{x \rightarrow +\infty}\left (x \sqrt{ 1-\frac{a}{x} }+ax \right )={ \lim_{x \rightarrow +\infty}\left [ x \left ( \sqrt{1+\frac{a}{x}}+a \right ) \right ]=+\infty(1+a)](/forum/ext/geomar/texintegr/latexrender/pictures/5367a9bd301066c020b8a3f33f0b6977.png)
Διακρίνω περιπτώσεις:
1.

Σε αυτήν την περίπτωση το όριο είναι ίσο με
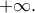
2.

Σε αυτήν την περίπτωση το όριο είναι ίσο με

3.Εξετάζω τι γίνεται για

Σε αυτήν την περίπτωση


Aναγκαστικά λοιπόν

Δ2. Η εφαπτομένη της γραφικής παράστασης της
 στο τυχαίο σημείο της
στο τυχαίο σημείο της 
έχει εξίσωση

H εν λόγω εφαπτομένη διέρχεται από το σημείο
 αν και μόνον αν
αν και μόνον αν
H εφαπτομένη της γραφικής παράστασης της
 στο σημείο της
στο σημείο της 
έχει εξίσωση

Θα αποδειχθεί ότι η ευθεία αυτή εφάπτεται στη γραφική παράσταση της
 .
.
Θα θέλαμε ένα σημείο
 τέτοιο ώστε
τέτοιο ώστε 
H εφαπτομένη της γραφικής παράστασης της
 στο σημείο της
στο σημείο της 
έχει εξίσωση

Δ3. Αυτό που θέλουμε να αποδειχθεί είναι η ανισότητα
 για κάθε
για κάθε 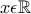
Ασφαλώς ξέρουμε ότι

με την ισότητα αν και μόνον αν
 .
.Eπίσης

με την ισότητα αν και μόνον αν
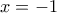 .
.Έτσι μπορεί να γραφεί άφοβα ότι
 για κάθε
για κάθε 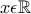
Δ4. Έστω η συνάρτηση
![H\left ( x \right )=\left ( x-k-1 \right )\left [ f\left ( x-1 \right ) -x\right ]+\left ( x-k \right )\left [ f\left ( x \right )-g\left ( x \right ) \right ] H\left ( x \right )=\left ( x-k-1 \right )\left [ f\left ( x-1 \right ) -x\right ]+\left ( x-k \right )\left [ f\left ( x \right )-g\left ( x \right ) \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/2513a12a8f208bda987120d5ee607038.png)
με
![x\epsilon \left [ k,k+1 \right ] x\epsilon \left [ k,k+1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/2991aca17439ae6a92f4aa4ed1864977.png)
H
 είναι συνεχής στο
είναι συνεχής στο ![\left [ k,k+1 \right ] \left [ k,k+1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/ab07f3b7f823a40166b6f1d76a1da0de.png)

όπως είδαμε στο προηγούμενο σκέλος.

Γράφω αιτιολόγηση του αρνητικού προσήμου.
Eίναι βέβαιο ότι

με την ισότητα να ισχύει αν και μόνον αν
 .
.H τιμή όμως αυτή έχει εξαιρεθεί από τη διατύπωση του θέματος.
Αναγκαστικά λοιπόν

Σύμφωνα με το θεώρημα Bolzano υπάρχει ένα τουλάχιστον

τέτοιο ώστε
![H\left ( \rho \right )=0\Leftrightarrow \left ( \rho -k-1 \right )\left [ f\left ( \rho -1 \right )-\rho \right ]+\left ( \rho -k \right )\left [ f\left ( \rho \right )-g\left ( \rho \right ) \right ]=0\Leftrightarrow H\left ( \rho \right )=0\Leftrightarrow \left ( \rho -k-1 \right )\left [ f\left ( \rho -1 \right )-\rho \right ]+\left ( \rho -k \right )\left [ f\left ( \rho \right )-g\left ( \rho \right ) \right ]=0\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/7b116bb2a31a328b7e433df41f7ed1b0.png)

Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
