ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΟΜΟΓΕΝΩΝ 2020
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΡΑΤΟΣ
- Δημοσιεύσεις: 467
- Εγγραφή: Τρί Αύγ 04, 2009 12:16 pm
ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΟΜΟΓΕΝΩΝ 2020
Καλησπέρα,
Ανεβάζω τα θέματα επαναληπτικών εξετάσεων ημερήσιων λυκείων και ομογενών της 08-9-2020.
Εύχομαι καλή σχολική χρονιά με Υγεία !
Ανεβάζω τα θέματα επαναληπτικών εξετάσεων ημερήσιων λυκείων και ομογενών της 08-9-2020.
Εύχομαι καλή σχολική χρονιά με Υγεία !
- Συνημμένα
-
- ΘΕΜΑΤΑ ΟΜΟΓΕΝΩΝ - ΝΕΟ ΣΥΣΤΗΜΑ.pdf
- (192.47 KiB) Μεταφορτώθηκε 258 φορές
-
- ΘΕΜΑΤΑ ΟΜΟΓΕΝΩΝ - ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ.pdf
- (240.16 KiB) Μεταφορτώθηκε 171 φορές
-
- ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΗΜΕΡ&ΕΣΠΕΡ-ΝΕΟ ΣΥΣΤΗΜΑ.pdf
- (207.01 KiB) Μεταφορτώθηκε 247 φορές
-
- ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΗΜΕΡ&ΕΣΠΕΡ-ΠΑΛΙΟ ΣΥΣΤΗΜΑ.pdf
- (277.1 KiB) Μεταφορτώθηκε 176 φορές
Λέξεις Κλειδιά:
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1291
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΟΜΟΓΕΝΩΝ 2020
Θα γράψω μία λύση για το τέταρτο θέμα των επαναληπτικών των ημερησίων με το νέο σύστημα.
Το θέμα έχει ως εξής:
Έστω παραγωγίσιμη συνάρτηση για την οποία ισχύουν :
για την οποία ισχύουν :
 για κάθε
για κάθε  ,
,

Δ1. Να αποδείξετε ότι η συνάρτηση είναι σταθερή. Στη συνέχεια να αποδείξετε ότι
είναι σταθερή. Στη συνέχεια να αποδείξετε ότι 
MONAΔΕΣ 6
Δ2. Να αποδείξετε ότι η συνάρτηση παρουσιάζει μοναδικό ολικό ελάχιστο στο
παρουσιάζει μοναδικό ολικό ελάχιστο στο  το οποίο και να βρείτε.
το οποίο και να βρείτε.
MONAΔΕΣ 6
Δ3. Να αποδείξετε ότι η εξίσωση στο διάστημα
στο διάστημα 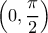 έχει ακριβώς δύο ρίζες
έχει ακριβώς δύο ρίζες 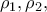 με
με 
MONAΔΕΣ 6
Δ4. Να αποδείξετε ότι όπου
όπου 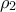 η ρίζα του ερωτήματος Δ3.
η ρίζα του ερωτήματος Δ3.
MONAΔΕΣ 7
ΛΥΣΗ
Δ1 Η δοσμένη ισότητα γράφεται ισοδύναμα
![\displaystyle \sigma \upsilon \nu ^{2}x\left [ f\left ( x \right )\sigma \upsilon \nu x+f'\left ( x \right )\eta \mu x \right ]=1\Leftrightarrow \displaystyle \sigma \upsilon \nu ^{2}x\left [ f\left ( x \right )\sigma \upsilon \nu x+f'\left ( x \right )\eta \mu x \right ]=1\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/8a77bcd098bba39f1fed101c66eafdd2.png)


![\left [ f\left ( x \right )\eta \mu x \right ]'=\left ( \varepsilon \varphi x \right )' \left [ f\left ( x \right )\eta \mu x \right ]'=\left ( \varepsilon \varphi x \right )'](/forum/ext/geomar/texintegr/latexrender/pictures/19a49fa894b27932641e70a5610e0812.png) για κάθε
για κάθε 
Άρα μπορώ να γράψω ότι ισχύει στο διάστημα αυτό , όπου
, όπου  σταθερά.
σταθερά.
Για προκύπτει ότι
προκύπτει ότι

Άρα για κάθε ισχύει
ισχύει 
Πλέον είναι πολύ εύκολο να αποδειχθεί ότι η συνάρτηση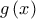 είναι σταθερή στο
είναι σταθερή στο 

Δ2

Αφού έχουμε ότι
έχουμε ότι 
Έτσι λοιπόν
Συνεπώς η εξίσωση γράφεται ισοδύναμα
H μοναδική λύση της εξίσωσης αυτής στο είναι η
είναι η 
Θα εξεταστεί η μονοτονία της στα διαστήματα
στα διαστήματα  και
και 


Με αντίστοιχες σκέψεις συμπεραίνει κάποιος ότι
Στην επίλυση των παραπάνω ανισώσεων ελήφθη υπ' όψιν το γεγονός ότι η συνάρτηση ''εφαπτομένη'' είναι γνησίως αύξουσα στο
Το πρόσημο της μπορεί να βρεθεί και διαφορετικά, ας το δούμε...
μπορεί να βρεθεί και διαφορετικά, ας το δούμε...
Η είναι συνεχής στο
είναι συνεχής στο  , άρα το πρόσημό της στο
, άρα το πρόσημό της στο  είναι το ίδιο με το πρόσημο της τιμής της σε κάποιο σημείο του διαστήματος αυτού.
είναι το ίδιο με το πρόσημο της τιμής της σε κάποιο σημείο του διαστήματος αυτού.

Η είναι συνεχής στο
είναι συνεχής στο  , άρα το πρόσημό της στο
, άρα το πρόσημό της στο  είναι το ίδιο με το πρόσημο της τιμής της σε κάποιο σημείο του διαστήματος αυτού.
είναι το ίδιο με το πρόσημο της τιμής της σε κάποιο σημείο του διαστήματος αυτού.

Έτσι λοιπόν η είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  και γνησίως αύξουσα στο
και γνησίως αύξουσα στο  , άρα εμφανίζει ολικό ελάχιστο στο
, άρα εμφανίζει ολικό ελάχιστο στο  με τιμή
με τιμή

Δ3 Ισχύει ότι
και ότι
Αυτό σημαίνει ότι η συνεχής συνάρτηση απεικονίζει το διάστημα
απεικονίζει το διάστημα ![\displaystyle\left ( 0,\frac{\pi }{4} \right ] \displaystyle\left ( 0,\frac{\pi }{4} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/623e8b7b9ebb260d6d70bfde93a52fe5.png) , στο οποίο είναι γνησίως
, στο οποίο είναι γνησίως
φθίνουσα, στο και το διάστημα
και το διάστημα  ,στο οποίο
,στο οποίο
είναι γνησίως αύξουσα, πάλι στο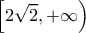 . Φυσικά
. Φυσικά 
Έτσι λοιπόν υπάρχει ακριβώς ένα τέτοιο ώστε
τέτοιο ώστε  και ακριβώς ένα
και ακριβώς ένα  τέτοιο ώστε
τέτοιο ώστε  Φυσικά
Φυσικά 
Δ4 Για την ισχύουν οι δύο συνθήκες για να ισχύει το Θεώρημα Μέσης Τιμής του Διαφορικού Λογισμού στο
ισχύουν οι δύο συνθήκες για να ισχύει το Θεώρημα Μέσης Τιμής του Διαφορικού Λογισμού στο ![\displaystyle \left [ \frac{\pi }{4},\rho _{2} \right ] \displaystyle \left [ \frac{\pi }{4},\rho _{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/dd41275989caa6a5e312523c97836c57.png) . Άρα υπάρχει ένα τουλάχιστον
. Άρα υπάρχει ένα τουλάχιστον  τέτοιο ώστε
τέτοιο ώστε 
Συνεπώς για αυτό το ισχύει ότι
ισχύει ότι  .
.
Έχουμε δει ότι
Έτσι λοιπόν για κάθε
για κάθε 
Συνεπώς η είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
Έτσι .
.
Νομίζω ότι όλοι καταλαβαίνουν ότι αφού
αφού  κι έτσι η φορά της διάταξης μένει ίδια...
κι έτσι η φορά της διάταξης μένει ίδια...
Στα όσα έχω γράψει θα ήθελα να κάνω μία προσθήκη: Έχει η γραφική παράσταση της άξονα συμμετρίας;
άξονα συμμετρίας;
Αν τουλάχιστον ένα παιδί ωφεληθεί από αυτήν τη δημοσίευση, θα μείνω ικανοποιημένος...
Το θέμα έχει ως εξής:
Έστω παραγωγίσιμη συνάρτηση
 για την οποία ισχύουν :
για την οποία ισχύουν : για κάθε
για κάθε  ,
,
Δ1. Να αποδείξετε ότι η συνάρτηση
 είναι σταθερή. Στη συνέχεια να αποδείξετε ότι
είναι σταθερή. Στη συνέχεια να αποδείξετε ότι 
MONAΔΕΣ 6
Δ2. Να αποδείξετε ότι η συνάρτηση
 παρουσιάζει μοναδικό ολικό ελάχιστο στο
παρουσιάζει μοναδικό ολικό ελάχιστο στο  το οποίο και να βρείτε.
το οποίο και να βρείτε.MONAΔΕΣ 6
Δ3. Να αποδείξετε ότι η εξίσωση
 στο διάστημα
στο διάστημα 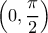 έχει ακριβώς δύο ρίζες
έχει ακριβώς δύο ρίζες 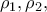 με
με 
MONAΔΕΣ 6
Δ4. Να αποδείξετε ότι
 όπου
όπου 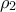 η ρίζα του ερωτήματος Δ3.
η ρίζα του ερωτήματος Δ3.MONAΔΕΣ 7
ΛΥΣΗ
Δ1 Η δοσμένη ισότητα γράφεται ισοδύναμα
![\displaystyle \sigma \upsilon \nu ^{2}x\left [ f\left ( x \right )\sigma \upsilon \nu x+f'\left ( x \right )\eta \mu x \right ]=1\Leftrightarrow \displaystyle \sigma \upsilon \nu ^{2}x\left [ f\left ( x \right )\sigma \upsilon \nu x+f'\left ( x \right )\eta \mu x \right ]=1\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/8a77bcd098bba39f1fed101c66eafdd2.png)


![\left [ f\left ( x \right )\eta \mu x \right ]'=\left ( \varepsilon \varphi x \right )' \left [ f\left ( x \right )\eta \mu x \right ]'=\left ( \varepsilon \varphi x \right )'](/forum/ext/geomar/texintegr/latexrender/pictures/19a49fa894b27932641e70a5610e0812.png) για κάθε
για κάθε 
Άρα μπορώ να γράψω ότι ισχύει στο διάστημα αυτό
 , όπου
, όπου  σταθερά.
σταθερά.Για
 προκύπτει ότι
προκύπτει ότι 
Άρα για κάθε
 ισχύει
ισχύει 
Πλέον είναι πολύ εύκολο να αποδειχθεί ότι η συνάρτηση
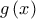 είναι σταθερή στο
είναι σταθερή στο 

Δ2


Αφού
 έχουμε ότι
έχουμε ότι 
Έτσι λοιπόν

Συνεπώς η εξίσωση γράφεται ισοδύναμα

H μοναδική λύση της εξίσωσης αυτής στο
 είναι η
είναι η 
Θα εξεταστεί η μονοτονία της
 στα διαστήματα
στα διαστήματα  και
και 


Με αντίστοιχες σκέψεις συμπεραίνει κάποιος ότι

Στην επίλυση των παραπάνω ανισώσεων ελήφθη υπ' όψιν το γεγονός ότι η συνάρτηση ''εφαπτομένη'' είναι γνησίως αύξουσα στο

Το πρόσημο της
 μπορεί να βρεθεί και διαφορετικά, ας το δούμε...
μπορεί να βρεθεί και διαφορετικά, ας το δούμε...Η
 είναι συνεχής στο
είναι συνεχής στο  , άρα το πρόσημό της στο
, άρα το πρόσημό της στο  είναι το ίδιο με το πρόσημο της τιμής της σε κάποιο σημείο του διαστήματος αυτού.
είναι το ίδιο με το πρόσημο της τιμής της σε κάποιο σημείο του διαστήματος αυτού.
Η
 είναι συνεχής στο
είναι συνεχής στο  , άρα το πρόσημό της στο
, άρα το πρόσημό της στο  είναι το ίδιο με το πρόσημο της τιμής της σε κάποιο σημείο του διαστήματος αυτού.
είναι το ίδιο με το πρόσημο της τιμής της σε κάποιο σημείο του διαστήματος αυτού.
Έτσι λοιπόν η
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  και γνησίως αύξουσα στο
και γνησίως αύξουσα στο  , άρα εμφανίζει ολικό ελάχιστο στο
, άρα εμφανίζει ολικό ελάχιστο στο  με τιμή
με τιμή 
Δ3 Ισχύει ότι

και ότι

Αυτό σημαίνει ότι η συνεχής συνάρτηση
 απεικονίζει το διάστημα
απεικονίζει το διάστημα ![\displaystyle\left ( 0,\frac{\pi }{4} \right ] \displaystyle\left ( 0,\frac{\pi }{4} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/623e8b7b9ebb260d6d70bfde93a52fe5.png) , στο οποίο είναι γνησίως
, στο οποίο είναι γνησίως φθίνουσα, στο
 και το διάστημα
και το διάστημα  ,στο οποίο
,στο οποίο είναι γνησίως αύξουσα, πάλι στο
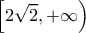 . Φυσικά
. Φυσικά 
Έτσι λοιπόν υπάρχει ακριβώς ένα
 τέτοιο ώστε
τέτοιο ώστε  και ακριβώς ένα
και ακριβώς ένα  τέτοιο ώστε
τέτοιο ώστε  Φυσικά
Φυσικά 
Δ4 Για την
 ισχύουν οι δύο συνθήκες για να ισχύει το Θεώρημα Μέσης Τιμής του Διαφορικού Λογισμού στο
ισχύουν οι δύο συνθήκες για να ισχύει το Θεώρημα Μέσης Τιμής του Διαφορικού Λογισμού στο ![\displaystyle \left [ \frac{\pi }{4},\rho _{2} \right ] \displaystyle \left [ \frac{\pi }{4},\rho _{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/dd41275989caa6a5e312523c97836c57.png) . Άρα υπάρχει ένα τουλάχιστον
. Άρα υπάρχει ένα τουλάχιστον  τέτοιο ώστε
τέτοιο ώστε 
Συνεπώς για αυτό το
 ισχύει ότι
ισχύει ότι  .
.Έχουμε δει ότι

Έτσι λοιπόν
 για κάθε
για κάθε 
Συνεπώς η
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
Έτσι
 .
.Νομίζω ότι όλοι καταλαβαίνουν ότι
 αφού
αφού  κι έτσι η φορά της διάταξης μένει ίδια...
κι έτσι η φορά της διάταξης μένει ίδια...Στα όσα έχω γράψει θα ήθελα να κάνω μία προσθήκη: Έχει η γραφική παράσταση της
 άξονα συμμετρίας;
άξονα συμμετρίας;Αν τουλάχιστον ένα παιδί ωφεληθεί από αυτήν τη δημοσίευση, θα μείνω ικανοποιημένος...
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΟΜΟΓΕΝΩΝ 2020
Δίνω τη γραφική παράσταση τηςΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Τρί Μάιος 25, 2021 6:54 pmΘα γράψω μία λύση για το τέταρτο θέμα των επαναληπτικών των ημερησίων με το νέο σύστημα.
Το θέμα έχει ως εξής:
Έστω παραγωγίσιμη συνάρτησηγια την οποία ισχύουν :
για κάθε
,
Δ1. Να αποδείξετε ότι η συνάρτησηείναι σταθερή. Στη συνέχεια να αποδείξετε ότι
MONAΔΕΣ 6
Δ2. Να αποδείξετε ότι η συνάρτησηπαρουσιάζει μοναδικό ολικό ελάχιστο στο
το οποίο και να βρείτε.
MONAΔΕΣ 6
Δ3. Να αποδείξετε ότι η εξίσωσηστο διάστημα
έχει ακριβώς δύο ρίζες
με
MONAΔΕΣ 6
Δ4. Να αποδείξετε ότιόπου
η ρίζα του ερωτήματος Δ3.
MONAΔΕΣ 7
ΛΥΣΗ
Δ1 Η δοσμένη ισότητα γράφεται ισοδύναμα
για κάθε
Άρα μπορώ να γράψω ότι ισχύει στο διάστημα αυτό, όπου
σταθερά.
Γιαπροκύπτει ότι
Άρα για κάθεισχύει
Πλέον είναι πολύ εύκολο να αποδειχθεί ότι η συνάρτησηείναι σταθερή στο
Δ2
Αφούέχουμε ότι
Έτσι λοιπόν
Συνεπώς η εξίσωση γράφεται ισοδύναμα
H μοναδική λύση της εξίσωσης αυτής στοείναι η
Θα εξεταστεί η μονοτονία τηςστα διαστήματα
και
Με αντίστοιχες σκέψεις συμπεραίνει κάποιος ότι
Στην επίλυση των παραπάνω ανισώσεων ελήφθη υπ' όψιν το γεγονός ότι η συνάρτηση ''εφαπτομένη'' είναι γνησίως αύξουσα στο
Το πρόσημο τηςμπορεί να βρεθεί και διαφορετικά, ας το δούμε...
Ηείναι συνεχής στο
, άρα το πρόσημό της στο
είναι το ίδιο με το πρόσημο της τιμής της σε κάποιο σημείο του διαστήματος αυτού.
Ηείναι συνεχής στο
, άρα το πρόσημό της στο
είναι το ίδιο με το πρόσημο της τιμής της σε κάποιο σημείο του διαστήματος αυτού.
Έτσι λοιπόν ηείναι γνησίως φθίνουσα στο
και γνησίως αύξουσα στο
, άρα εμφανίζει ολικό ελάχιστο στο
με τιμή
Δ3 Ισχύει ότι
και ότι
Αυτό σημαίνει ότι η συνεχής συνάρτησηαπεικονίζει το διάστημα
, στο οποίο είναι γνησίως
φθίνουσα, στοκαι το διάστημα
,στο οποίο
είναι γνησίως αύξουσα, πάλι στο. Φυσικά
Έτσι λοιπόν υπάρχει ακριβώς ένατέτοιο ώστε
και ακριβώς ένα
τέτοιο ώστε
Φυσικά
Δ4 Για τηνισχύουν οι δύο συνθήκες για να ισχύει το Θεώρημα Μέσης Τιμής του Διαφορικού Λογισμού στο
. Άρα υπάρχει ένα τουλάχιστον
τέτοιο ώστε
Συνεπώς για αυτό τοισχύει ότι
.
Έχουμε δει ότι
Έτσι λοιπόνγια κάθε
Συνεπώς ηείναι γνησίως αύξουσα στο
Έτσι.
Νομίζω ότι όλοι καταλαβαίνουν ότιαφού
κι έτσι η φορά της διάταξης μένει ίδια...
Στα όσα έχω γράψει θα ήθελα να κάνω μία προσθήκη: Έχει η γραφική παράσταση τηςάξονα συμμετρίας;
Αν τουλάχιστον ένα παιδί ωφεληθεί από αυτήν τη δημοσίευση, θα μείνω ικανοποιημένος...

-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1291
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΟΜΟΓΕΝΩΝ 2020
Να ευχαριστήσω το Γιώργο για τη γραφική παράσταση που δημοσίευσε.
Θα ήθελα να δοθεί λεπτομερής λύση στο πρόσθετο ερώτημα που έθεσα: Έχει η γραφική παράσταση της άξονα συμμετρίας;
άξονα συμμετρίας;
Εποπτικά είναι εύκολο πλέον να δοθεί απάντηση, σκεφθείτε όμως να ήταν σκέλος του θέματος. Πώς θα το διαπραγματευόταν κάποιος πετυχημένα;
Ας το δούμε για χάρη των παιδιών...
Θα ήθελα να δοθεί λεπτομερής λύση στο πρόσθετο ερώτημα που έθεσα: Έχει η γραφική παράσταση της
 άξονα συμμετρίας;
άξονα συμμετρίας;Εποπτικά είναι εύκολο πλέον να δοθεί απάντηση, σκεφθείτε όμως να ήταν σκέλος του θέματος. Πώς θα το διαπραγματευόταν κάποιος πετυχημένα;
Ας το δούμε για χάρη των παιδιών...
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13277
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΟΜΟΓΕΝΩΝ 2020
ΘΕΜΑ Γ
Δίνεται η συνεχής συνάρτηση με τύπο
με τύπο  .
.
Γ1. Να αποδείξετε ότι από το σημείο διέρχονται δύο ακριβώς εφαπτομένες της γραφικής παράστασης της f και να βρείτε τις εξισώσεις τους.......... Μονάδες 8
διέρχονται δύο ακριβώς εφαπτομένες της γραφικής παράστασης της f και να βρείτε τις εξισώσεις τους.......... Μονάδες 8
Γ2. Έστω η μία από τις δύο εφαπτομένες του ερωτήματος Γ1. Έστω ακόμα
η μία από τις δύο εφαπτομένες του ερωτήματος Γ1. Έστω ακόμα  ευθεία η οποία είναι παράλληλη στην
ευθεία η οποία είναι παράλληλη στην  και διέρχεται από το σημείο
και διέρχεται από το σημείο  με
με  . Να αποδείξετε ότι ανάμεσα στις ευθείες
. Να αποδείξετε ότι ανάμεσα στις ευθείες 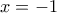 και
και  υπάρχει ακριβώς ένα σημείο τομής της
υπάρχει ακριβώς ένα σημείο τομής της  με τη γραφική παράσταση της
με τη γραφική παράσταση της  . .......... Μονάδες 9
. .......... Μονάδες 9
Γ3. Ένα υλικό σημείο κινείται κατά μήκος της καμπύλης
κινείται κατά μήκος της καμπύλης  με ρυθμό μεταβολής της τετμημένης του
με ρυθμό μεταβολής της τετμημένης του  . Το σημείο
. Το σημείο  ξεκινά από το σημείο
ξεκινά από το σημείο  και καταλήγει στην αρχή τω αξόνων
και καταλήγει στην αρχή τω αξόνων  . Σε ποιο σημείο της καμπύλης ο ρυθμός μεταβολής της τεταγμένης του σημείου
. Σε ποιο σημείο της καμπύλης ο ρυθμός μεταβολής της τεταγμένης του σημείου  είναι τριπλάσιος του ρυθμού μεταβολής της τετμημένης του; ............... Μονάδες 8
είναι τριπλάσιος του ρυθμού μεταβολής της τετμημένης του; ............... Μονάδες 8
Λύση
Γ1. Έστω
Έστω  η εφαπτομένη της
η εφαπτομένη της  στο σημείο
στο σημείο 
Οι συντεταγμένες του επαληθεύουν την εξίσωση
επαληθεύουν την εξίσωση  άρα:
άρα:
 ή
ή 
Έχουμε λοιπόν δύο εφαπτόμενες με εξισώσεις και
και 
Γ2. Είναι η άσκηση της Β' ΟΜΑΔΑΣ του σχολικού βιβλίου στο κεφάλαιο "Συνέπειες του ΘΜΤ".
της Β' ΟΜΑΔΑΣ του σχολικού βιβλίου στο κεφάλαιο "Συνέπειες του ΘΜΤ".
Γ3. και
και 
Έστω η χρονική στιγμή όπου η τεταγμένη του
η χρονική στιγμή όπου η τεταγμένη του  έχει ρυθμό μεταβολής τριπλάσιο της τετμημένης του.
έχει ρυθμό μεταβολής τριπλάσιο της τετμημένης του.

κι επειδή θα είναι
θα είναι  και το ζητούμενο σημείο
και το ζητούμενο σημείο 
Σχόλια:
1. Το ερώτημα Γ2 είναι άσκηση του σχολικού βιβλίου, κάτι που παρατηρούμε όλο και συχνότερα τα τελευταία χρόνια και κατά την άποψή μου αποτελεί θετικό στοιχείο.
2. Το ελληνικό αλφάβητο έχει (δόξα τω Θεώ) 24 γράμματα. Πώς είναι δυνατόν να επιλεχθεί το γράμμα Μ για δύο διαφορετικά σημεία στην ίδια άσκηση;
Δίνεται η συνεχής συνάρτηση
 με τύπο
με τύπο  .
.Γ1. Να αποδείξετε ότι από το σημείο
 διέρχονται δύο ακριβώς εφαπτομένες της γραφικής παράστασης της f και να βρείτε τις εξισώσεις τους.......... Μονάδες 8
διέρχονται δύο ακριβώς εφαπτομένες της γραφικής παράστασης της f και να βρείτε τις εξισώσεις τους.......... Μονάδες 8Γ2. Έστω
 η μία από τις δύο εφαπτομένες του ερωτήματος Γ1. Έστω ακόμα
η μία από τις δύο εφαπτομένες του ερωτήματος Γ1. Έστω ακόμα  ευθεία η οποία είναι παράλληλη στην
ευθεία η οποία είναι παράλληλη στην  και διέρχεται από το σημείο
και διέρχεται από το σημείο  με
με  . Να αποδείξετε ότι ανάμεσα στις ευθείες
. Να αποδείξετε ότι ανάμεσα στις ευθείες 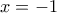 και
και  υπάρχει ακριβώς ένα σημείο τομής της
υπάρχει ακριβώς ένα σημείο τομής της  με τη γραφική παράσταση της
με τη γραφική παράσταση της  . .......... Μονάδες 9
. .......... Μονάδες 9Γ3. Ένα υλικό σημείο
 κινείται κατά μήκος της καμπύλης
κινείται κατά μήκος της καμπύλης  με ρυθμό μεταβολής της τετμημένης του
με ρυθμό μεταβολής της τετμημένης του  . Το σημείο
. Το σημείο  ξεκινά από το σημείο
ξεκινά από το σημείο  και καταλήγει στην αρχή τω αξόνων
και καταλήγει στην αρχή τω αξόνων  . Σε ποιο σημείο της καμπύλης ο ρυθμός μεταβολής της τεταγμένης του σημείου
. Σε ποιο σημείο της καμπύλης ο ρυθμός μεταβολής της τεταγμένης του σημείου  είναι τριπλάσιος του ρυθμού μεταβολής της τετμημένης του; ............... Μονάδες 8
είναι τριπλάσιος του ρυθμού μεταβολής της τετμημένης του; ............... Μονάδες 8Λύση
Γ1.
 Έστω
Έστω  η εφαπτομένη της
η εφαπτομένη της  στο σημείο
στο σημείο 
Οι συντεταγμένες του
 επαληθεύουν την εξίσωση
επαληθεύουν την εξίσωση  άρα:
άρα: ή
ή 
Έχουμε λοιπόν δύο εφαπτόμενες με εξισώσεις
 και
και 
Γ2. Είναι η άσκηση
 της Β' ΟΜΑΔΑΣ του σχολικού βιβλίου στο κεφάλαιο "Συνέπειες του ΘΜΤ".
της Β' ΟΜΑΔΑΣ του σχολικού βιβλίου στο κεφάλαιο "Συνέπειες του ΘΜΤ".Γ3.
 και
και 
Έστω
 η χρονική στιγμή όπου η τεταγμένη του
η χρονική στιγμή όπου η τεταγμένη του  έχει ρυθμό μεταβολής τριπλάσιο της τετμημένης του.
έχει ρυθμό μεταβολής τριπλάσιο της τετμημένης του.
κι επειδή
 θα είναι
θα είναι  και το ζητούμενο σημείο
και το ζητούμενο σημείο 
Σχόλια:
1. Το ερώτημα Γ2 είναι άσκηση του σχολικού βιβλίου, κάτι που παρατηρούμε όλο και συχνότερα τα τελευταία χρόνια και κατά την άποψή μου αποτελεί θετικό στοιχείο.
2. Το ελληνικό αλφάβητο έχει (δόξα τω Θεώ) 24 γράμματα. Πώς είναι δυνατόν να επιλεχθεί το γράμμα Μ για δύο διαφορετικά σημεία στην ίδια άσκηση;
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1291
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΟΜΟΓΕΝΩΝ 2020
O Γιώργος Βισβίκης έκανε πολύ καλά που έλυσε το τρίτο θέμα από τις επαναληπτικές πανελλήνιες του 2020 με το νέο σύστημα. Τα θέματα των επαναληπτικών ας μην τα προσπερνάμε...
Είχα θέσει ένα ερώτημα τελειώνοντας τη δημοσίευση της λύσης του τέταρτου θέματος από τις επαναληπτικές πανελλήνιες του 2020 με το νέο σύστημα.
Έχει η γραφική παράσταση της άξονα συμμετρίας;
άξονα συμμετρίας;
Από τη γραφική παράσταση που δημοσίευσε ο Γιώργος Βισβίκης φαίνεται ότι η ευθεία αποτελεί απάντηση στο ερώτημα. Πώς όμως αυτό αποδεικνύεται;
αποτελεί απάντηση στο ερώτημα. Πώς όμως αυτό αποδεικνύεται;
Πρώτα πρέπει να αποδειχθεί ότι το πεδίο ορισμού της είναι ''συμμετρικό'' ως προς το
είναι ''συμμετρικό'' ως προς το  . Η λέξη που μπήκε σε εισαγωγικά μπήκε γιατί είναι μάλλον αδόκιμη, ουδέποτε την είδα κάπου γραμμένη σε παρόμοιο θέμα...
. Η λέξη που μπήκε σε εισαγωγικά μπήκε γιατί είναι μάλλον αδόκιμη, ουδέποτε την είδα κάπου γραμμένη σε παρόμοιο θέμα...

Μετά, χρησιμοποιώντας τα γνωστά από την Τριγωνομετρία και τα συμπληρωματικά τόξα, μπορούμε αμέσως να αποδείξουμε ότι
 .
.
Άρα η ευθεία είναι άξονας συμμετρίας της γραφικής παράστασης της
είναι άξονας συμμετρίας της γραφικής παράστασης της  .
.
Ένα άλλο ωραίο συμπέρασμα που προκύπτει είναι το εξής:
Να αποδειχθεί ότι
Το ζητούμενο αυτό είναι εκτός ύλης μετά τις περικοπές που έγιναν για το 2020 και το 2021.
Η ύλη της Ανάλυσης της Τρίτης Λυκείου ανέκαθεν περιλάμβανε τις άρτιες και τις περιττές συναρτήσεις και τις όμορφες συμμετρίες που πηγάζουν από αυτές. Εδώ βλέπουμε μια συμμετρία σε συνάρτηση που δεν περιλαμβάνεται στις δύο αυτές περιπτώσεις.
Είχα θέσει ένα ερώτημα τελειώνοντας τη δημοσίευση της λύσης του τέταρτου θέματος από τις επαναληπτικές πανελλήνιες του 2020 με το νέο σύστημα.
Έχει η γραφική παράσταση της
 άξονα συμμετρίας;
άξονα συμμετρίας;Από τη γραφική παράσταση που δημοσίευσε ο Γιώργος Βισβίκης φαίνεται ότι η ευθεία
 αποτελεί απάντηση στο ερώτημα. Πώς όμως αυτό αποδεικνύεται;
αποτελεί απάντηση στο ερώτημα. Πώς όμως αυτό αποδεικνύεται;Πρώτα πρέπει να αποδειχθεί ότι το πεδίο ορισμού της
 είναι ''συμμετρικό'' ως προς το
είναι ''συμμετρικό'' ως προς το  . Η λέξη που μπήκε σε εισαγωγικά μπήκε γιατί είναι μάλλον αδόκιμη, ουδέποτε την είδα κάπου γραμμένη σε παρόμοιο θέμα...
. Η λέξη που μπήκε σε εισαγωγικά μπήκε γιατί είναι μάλλον αδόκιμη, ουδέποτε την είδα κάπου γραμμένη σε παρόμοιο θέμα...
Μετά, χρησιμοποιώντας τα γνωστά από την Τριγωνομετρία και τα συμπληρωματικά τόξα, μπορούμε αμέσως να αποδείξουμε ότι
 .
. Άρα η ευθεία
 είναι άξονας συμμετρίας της γραφικής παράστασης της
είναι άξονας συμμετρίας της γραφικής παράστασης της  .
.Ένα άλλο ωραίο συμπέρασμα που προκύπτει είναι το εξής:
Να αποδειχθεί ότι

Το ζητούμενο αυτό είναι εκτός ύλης μετά τις περικοπές που έγιναν για το 2020 και το 2021.
Η ύλη της Ανάλυσης της Τρίτης Λυκείου ανέκαθεν περιλάμβανε τις άρτιες και τις περιττές συναρτήσεις και τις όμορφες συμμετρίες που πηγάζουν από αυτές. Εδώ βλέπουμε μια συμμετρία σε συνάρτηση που δεν περιλαμβάνεται στις δύο αυτές περιπτώσεις.
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΟΜΟΓΕΝΩΝ 2020
Θα μπορούσαμε να δυσκολέψουμε λίγο ακόμα το ερώτημα, ζητώντας να βρεθούν οι άξονες συμμετρίας της γραφικής παράστασης της συνάρτησης.ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Σάβ Μάιος 29, 2021 11:12 am
Είχα θέσει ένα ερώτημα τελειώνοντας τη δημοσίευση της λύσης του τέταρτου θέματος από τις επαναληπτικές πανελλήνιες του 2020 με το νέο σύστημα.
Έχει η γραφική παράσταση τηςάξονα συμμετρίας;
-
ΚΕΦΑΛΟΝΙΤΗΣ
- Δημοσιεύσεις: 1291
- Εγγραφή: Δευ Δεκ 28, 2009 11:41 pm
- Τοποθεσία: Kάπου στο πιο μεγάλο νησί του Ιονίου
Re: ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΟΜΟΓΕΝΩΝ 2020
Στην παρούσα δημοσίευση θα δούμε το τέταρτο θέμα από τις Επαναληπτικές Πανελλήνιες Εξετάσεις του 2020 με το Παλιό Σύστημα. Νομίζω ότι αξίζει να του ρίξετε μια ματιά...
Έστω![\displaystyle f:\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]\rightarrow \mathbb{R} \displaystyle f:\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/e082bddff103b3d088ee047a245528a7.png) μια συνεχής συνάρτηση τέτοια, ώστε για κάθε
μια συνεχής συνάρτηση τέτοια, ώστε για κάθε ![\displaystyle x\epsilon \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle x\epsilon \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/143074ba7a6fea13ce8c76c415a4b042.png) να ισχύει :
να ισχύει :

Δ1. Να αποδείξετε ότι![f\left ( x \right ) =\begin{cases} \displaystyle \frac{\sigma \upsilon \nu x-1}{x}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ 0, x=0 \end{cases} f\left ( x \right ) =\begin{cases} \displaystyle \frac{\sigma \upsilon \nu x-1}{x}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ 0, x=0 \end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/333f332d38fc988b9614bb55851e5fd8.png)
MONAΔΕΣ 3
Δ2. Να υπολογίσετε το ολοκλήρωμα
MONAΔΕΣ 4
Δ3. Nα αποδείξετε ότι η συνάρτηση είναι γνησίως φθίνουσα στο διάστημα
είναι γνησίως φθίνουσα στο διάστημα ![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png)
MONAΔΕΣ 7
Δ4. Nα αποδείξετε ότι η εξίσωση
έχει ακριβώς δύο ρίζες στο διάστημα![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png)
MONAΔΕΣ 4
Δ5. Έστω μια αρχική συνάρτηση της
μια αρχική συνάρτηση της  στο διάστημα
στο διάστημα ![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png) με
με 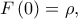 όπου
όπου  η μεγαλύτερη ρίζα της εξίσωσης του ερωτήματος (Δ4).
η μεγαλύτερη ρίζα της εξίσωσης του ερωτήματος (Δ4).
Να αποδείξετε ότι για κάθε![\displaystyle x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/011a431d7ba5538a169f6efe9761db4d.png) ισχύει
ισχύει 
MONAΔΕΣ 7
ΛΥΣΗ
Δ1. Aν τότε από τη δοσμένη ισότητα προκύπτει ότι
τότε από τη δοσμένη ισότητα προκύπτει ότι 
Aν τι γίνεται; Η
τι γίνεται; Η  είναι συνεχής στο
είναι συνεχής στο  από τα δεδομένα, συνεπώς
από τα δεδομένα, συνεπώς 
Έτσι![f\left ( x \right ) =\begin{cases} \displaystyle \frac{\sigma \upsilon \nu x-1}{x}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ 0, x=0 \end{cases} f\left ( x \right ) =\begin{cases} \displaystyle \frac{\sigma \upsilon \nu x-1}{x}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ 0, x=0 \end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/333f332d38fc988b9614bb55851e5fd8.png)
Δ2. H είναι ορισμένη στο διάστημα
είναι ορισμένη στο διάστημα ![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png) . Αυτό εξασφαλίζει ότι για κάθε
. Αυτό εξασφαλίζει ότι για κάθε ![\displaystyle x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/5fcf5742e3464ce61d2943f80ca94d14.png) θα ισχύει ότι
θα ισχύει ότι ![\displaystyle -x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle -x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7b370039d76cbb98511e45c180ae7778.png)
Για ισχύει ότι
ισχύει ότι 
Αυτό σημαίνει ότι η είναι περιττή στο διάστημα
είναι περιττή στο διάστημα ![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png) .
.
Άρα
Δ3. Θα εξεταστεί η παραγωγισιμότητα της στο
στο 

Για![\displaystyle x\epsilon \left [ -\frac{\pi }{2} ,0\right )\cup \left (0,\frac{\pi }{2} \right ] \displaystyle x\epsilon \left [ -\frac{\pi }{2} ,0\right )\cup \left (0,\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/775a16504dd32e677e2189230f2a5172.png) η
η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με

Έτσι μπορεί να γραφεί ότι![\displaystyle{f'\left ( x \right ) =\begin{cases} \displaystyle \frac{1-\sigma \upsilon \nu x-x\cdot \eta \mu x}{x^{2}}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ \displaystyle -\frac{1}{2}, x=0 \end{cases}} \displaystyle{f'\left ( x \right ) =\begin{cases} \displaystyle \frac{1-\sigma \upsilon \nu x-x\cdot \eta \mu x}{x^{2}}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ \displaystyle -\frac{1}{2}, x=0 \end{cases}}](/forum/ext/geomar/texintegr/latexrender/pictures/19c5f27421ffb65ac0a31e77a70da967.png)
Αυτό που οφείλω να αποδείξω είναι ότι για κάθε
για κάθε 

Στο ισχύει ότι
ισχύει ότι 
Έτσι στο διάστημα αυτό ισχύει ότι
Στο ισχύει ότι
ισχύει ότι 
Έτσι στο διάστημα αυτό ισχύει ότι
Συνεπώς ισχύει για κάθε
για κάθε 
Έτσι λοιπόν για κάθε
για κάθε  και έτσι η συνάρτηση
και έτσι η συνάρτηση  είναι γνησίως φθίνουσα στο διάστημα
είναι γνησίως φθίνουσα στο διάστημα ![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png)
Δ4. Mία προφανής ρίζα της δοσμένης εξίσωσης είναι το
H δοσμένη εξίσωση γράφεται ισοδύναμα φυσικά με
φυσικά με 

Ισχύει για την ότι
ότι ![\displaystyle \left [ -\frac{\pi }{2},0 \right )\rightarrow \left ( 0,\frac{2 }{\pi } \right ] \displaystyle \left [ -\frac{\pi }{2},0 \right )\rightarrow \left ( 0,\frac{2 }{\pi } \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/a53674f22c0cf3f4a670ec7036d05493.png) και
και
![\displaystyle\left ( 0,\frac{\pi }{2} \right ]\rightarrow \left [ -\frac{2}{\pi } ,0\right ) \displaystyle\left ( 0,\frac{\pi }{2} \right ]\rightarrow \left [ -\frac{2}{\pi } ,0\right )](/forum/ext/geomar/texintegr/latexrender/pictures/6fe03df21f77d88ce89c80621d13db6d.png) . Άρα η συνεχής συνάρτηση
. Άρα η συνεχής συνάρτηση  λαμβάνει τη
λαμβάνει τη
θετική τιμή για κάποιο
για κάποιο  η δε τιμή αυτή είναι και μοναδική γιατί η
η δε τιμή αυτή είναι και μοναδική γιατί η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
Δ5. Στο Δ4 είδαμε ότι η εξίσωση έχει δύο ακριβώς ρίζες, το και το
και το  με
με  Άρα
Άρα 
Ας δούμε τι γίνεται για εκείνα τα που ανήκουν στο
που ανήκουν στο 
Για την ισχύουν οι δύο συνθήκες του Θεωρήματος Μέσης Τιμής του Διαφορικού Λογισμού στο
ισχύουν οι δύο συνθήκες του Θεωρήματος Μέσης Τιμής του Διαφορικού Λογισμού στο ![\left [ x,0 \right ] \left [ x,0 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/43dd48e5a7d3af210d66c676c7897aee.png)
Άρα υπάρχει ένα τουλάχιστον τέτοιο ώστε
τέτοιο ώστε  , δηλαδή υπάρχει ένα τουλάχιστον
, δηλαδή υπάρχει ένα τουλάχιστον  τέτοιο ώστε
τέτοιο ώστε 
Όμως είδαμε ότι το πεδίο τιμών της είναι το
είναι το ![\displaystyle\left [ -\frac{2}{\pi } ,\frac{2}{\pi }\right ] \displaystyle\left [ -\frac{2}{\pi } ,\frac{2}{\pi }\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/2e9517a8cbb463a8da2fbba844f66e13.png) , άρα
, άρα

Για να μη σας κουράζω γράφοντας πολλά, αντίστοιχες σκέψεις κάνω για τα που ανήκουν στο διάστημα
που ανήκουν στο διάστημα ![\displaystyle\left ( 0,\frac{\pi }{2} \right ] \displaystyle\left ( 0,\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/18a765bdf678310ad153cbe479a01c44.png) βρίσκοντας ένα αντίστοιχο
βρίσκοντας ένα αντίστοιχο  και καταλήγω στην ίδια ανισότητα.
και καταλήγω στην ίδια ανισότητα.
Φυσικά για ισχύει η ισότητα. Αποδείχθηκε αυτό που ζητιόταν για κάθε
ισχύει η ισότητα. Αποδείχθηκε αυτό που ζητιόταν για κάθε ![\displaystyle x\epsilon \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle x\epsilon \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/46fc7d718461e26d40c741b89c9a4664.png)
Έστω
![\displaystyle f:\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]\rightarrow \mathbb{R} \displaystyle f:\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/e082bddff103b3d088ee047a245528a7.png) μια συνεχής συνάρτηση τέτοια, ώστε για κάθε
μια συνεχής συνάρτηση τέτοια, ώστε για κάθε ![\displaystyle x\epsilon \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle x\epsilon \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/143074ba7a6fea13ce8c76c415a4b042.png) να ισχύει :
να ισχύει :
Δ1. Να αποδείξετε ότι
![f\left ( x \right ) =\begin{cases} \displaystyle \frac{\sigma \upsilon \nu x-1}{x}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ 0, x=0 \end{cases} f\left ( x \right ) =\begin{cases} \displaystyle \frac{\sigma \upsilon \nu x-1}{x}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ 0, x=0 \end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/333f332d38fc988b9614bb55851e5fd8.png)
MONAΔΕΣ 3
Δ2. Να υπολογίσετε το ολοκλήρωμα

MONAΔΕΣ 4
Δ3. Nα αποδείξετε ότι η συνάρτηση
 είναι γνησίως φθίνουσα στο διάστημα
είναι γνησίως φθίνουσα στο διάστημα ![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png)
MONAΔΕΣ 7
Δ4. Nα αποδείξετε ότι η εξίσωση

έχει ακριβώς δύο ρίζες στο διάστημα
![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png)
MONAΔΕΣ 4
Δ5. Έστω
 μια αρχική συνάρτηση της
μια αρχική συνάρτηση της  στο διάστημα
στο διάστημα ![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png) με
με 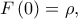 όπου
όπου  η μεγαλύτερη ρίζα της εξίσωσης του ερωτήματος (Δ4).
η μεγαλύτερη ρίζα της εξίσωσης του ερωτήματος (Δ4). Να αποδείξετε ότι για κάθε
![\displaystyle x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/011a431d7ba5538a169f6efe9761db4d.png) ισχύει
ισχύει 
MONAΔΕΣ 7
ΛΥΣΗ
Δ1. Aν
 τότε από τη δοσμένη ισότητα προκύπτει ότι
τότε από τη δοσμένη ισότητα προκύπτει ότι 
Aν
 τι γίνεται; Η
τι γίνεται; Η  είναι συνεχής στο
είναι συνεχής στο  από τα δεδομένα, συνεπώς
από τα δεδομένα, συνεπώς 
Έτσι
![f\left ( x \right ) =\begin{cases} \displaystyle \frac{\sigma \upsilon \nu x-1}{x}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ 0, x=0 \end{cases} f\left ( x \right ) =\begin{cases} \displaystyle \frac{\sigma \upsilon \nu x-1}{x}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ 0, x=0 \end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/333f332d38fc988b9614bb55851e5fd8.png)
Δ2. H
 είναι ορισμένη στο διάστημα
είναι ορισμένη στο διάστημα ![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png) . Αυτό εξασφαλίζει ότι για κάθε
. Αυτό εξασφαλίζει ότι για κάθε ![\displaystyle x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/5fcf5742e3464ce61d2943f80ca94d14.png) θα ισχύει ότι
θα ισχύει ότι ![\displaystyle -x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle -x\epsilon\left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7b370039d76cbb98511e45c180ae7778.png)
Για
 ισχύει ότι
ισχύει ότι 
Αυτό σημαίνει ότι η
 είναι περιττή στο διάστημα
είναι περιττή στο διάστημα ![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png) .
.Άρα

Δ3. Θα εξεταστεί η παραγωγισιμότητα της
 στο
στο 

Για
![\displaystyle x\epsilon \left [ -\frac{\pi }{2} ,0\right )\cup \left (0,\frac{\pi }{2} \right ] \displaystyle x\epsilon \left [ -\frac{\pi }{2} ,0\right )\cup \left (0,\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/775a16504dd32e677e2189230f2a5172.png) η
η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με 
Έτσι μπορεί να γραφεί ότι
![\displaystyle{f'\left ( x \right ) =\begin{cases} \displaystyle \frac{1-\sigma \upsilon \nu x-x\cdot \eta \mu x}{x^{2}}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ \displaystyle -\frac{1}{2}, x=0 \end{cases}} \displaystyle{f'\left ( x \right ) =\begin{cases} \displaystyle \frac{1-\sigma \upsilon \nu x-x\cdot \eta \mu x}{x^{2}}, x\epsilon \left [ -\frac{\pi }{2},0 \right )\cup \left (0,\frac{\pi }{2} \right ] \\ \displaystyle -\frac{1}{2}, x=0 \end{cases}}](/forum/ext/geomar/texintegr/latexrender/pictures/19c5f27421ffb65ac0a31e77a70da967.png)
Αυτό που οφείλω να αποδείξω είναι ότι
 για κάθε
για κάθε 

Στο
 ισχύει ότι
ισχύει ότι 
Έτσι στο διάστημα αυτό ισχύει ότι

Στο
 ισχύει ότι
ισχύει ότι 
Έτσι στο διάστημα αυτό ισχύει ότι

Συνεπώς ισχύει
 για κάθε
για κάθε 
Έτσι λοιπόν
 για κάθε
για κάθε  και έτσι η συνάρτηση
και έτσι η συνάρτηση  είναι γνησίως φθίνουσα στο διάστημα
είναι γνησίως φθίνουσα στο διάστημα ![\displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0670ab240c9ce8c32a0ed0118a127.png)
Δ4. Mία προφανής ρίζα της δοσμένης εξίσωσης είναι το

H δοσμένη εξίσωση γράφεται ισοδύναμα
 φυσικά με
φυσικά με 

Ισχύει για την
 ότι
ότι ![\displaystyle \left [ -\frac{\pi }{2},0 \right )\rightarrow \left ( 0,\frac{2 }{\pi } \right ] \displaystyle \left [ -\frac{\pi }{2},0 \right )\rightarrow \left ( 0,\frac{2 }{\pi } \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/a53674f22c0cf3f4a670ec7036d05493.png) και
και ![\displaystyle\left ( 0,\frac{\pi }{2} \right ]\rightarrow \left [ -\frac{2}{\pi } ,0\right ) \displaystyle\left ( 0,\frac{\pi }{2} \right ]\rightarrow \left [ -\frac{2}{\pi } ,0\right )](/forum/ext/geomar/texintegr/latexrender/pictures/6fe03df21f77d88ce89c80621d13db6d.png) . Άρα η συνεχής συνάρτηση
. Άρα η συνεχής συνάρτηση  λαμβάνει τη
λαμβάνει τηθετική τιμή
 για κάποιο
για κάποιο  η δε τιμή αυτή είναι και μοναδική γιατί η
η δε τιμή αυτή είναι και μοναδική γιατί η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
Δ5. Στο Δ4 είδαμε ότι η εξίσωση έχει δύο ακριβώς ρίζες, το
 και το
και το  με
με  Άρα
Άρα 
Ας δούμε τι γίνεται για εκείνα τα
 που ανήκουν στο
που ανήκουν στο 
Για την
 ισχύουν οι δύο συνθήκες του Θεωρήματος Μέσης Τιμής του Διαφορικού Λογισμού στο
ισχύουν οι δύο συνθήκες του Θεωρήματος Μέσης Τιμής του Διαφορικού Λογισμού στο ![\left [ x,0 \right ] \left [ x,0 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/43dd48e5a7d3af210d66c676c7897aee.png)
Άρα υπάρχει ένα τουλάχιστον
 τέτοιο ώστε
τέτοιο ώστε  , δηλαδή υπάρχει ένα τουλάχιστον
, δηλαδή υπάρχει ένα τουλάχιστον  τέτοιο ώστε
τέτοιο ώστε 
Όμως είδαμε ότι το πεδίο τιμών της
 είναι το
είναι το ![\displaystyle\left [ -\frac{2}{\pi } ,\frac{2}{\pi }\right ] \displaystyle\left [ -\frac{2}{\pi } ,\frac{2}{\pi }\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/2e9517a8cbb463a8da2fbba844f66e13.png) , άρα
, άρα 
Για να μη σας κουράζω γράφοντας πολλά, αντίστοιχες σκέψεις κάνω για τα
 που ανήκουν στο διάστημα
που ανήκουν στο διάστημα ![\displaystyle\left ( 0,\frac{\pi }{2} \right ] \displaystyle\left ( 0,\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/18a765bdf678310ad153cbe479a01c44.png) βρίσκοντας ένα αντίστοιχο
βρίσκοντας ένα αντίστοιχο  και καταλήγω στην ίδια ανισότητα.
και καταλήγω στην ίδια ανισότητα.Φυσικά για
 ισχύει η ισότητα. Αποδείχθηκε αυτό που ζητιόταν για κάθε
ισχύει η ισότητα. Αποδείχθηκε αυτό που ζητιόταν για κάθε ![\displaystyle x\epsilon \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ] \displaystyle x\epsilon \left [ -\frac{\pi }{2},\frac{\pi }{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/46fc7d718461e26d40c741b89c9a4664.png)
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
