Ενδεχομένως η ταξινόμηση να μην είναι η καλύτερη δυνατή αλλά μόλις συγκεντρώσω τις προταθείσες θα την βελτιώσω.
Χρησιμοποιούνται οι φάκελοι Γεωμετρίας A΄Λυκείου, Γεωμετρίας Juniors,Γεωμετρίας Seniors εως 01-01-2013
και Γεωμετρίας Β΄Λυκείου εως 01-01-2012 (με τον καιρό θα ανανεωθεί μιας και πέτυχα κι άλλες ασκήσεις στο 2ο πέρασμα των ίδιων φακέλων αλλά και άλλων)
Περιορισμένη χρήση κανόνα και διαβήτη
εύρεση μόνο με διαβήτη του σημείου τομής δυο τεμνόμενων ευθυγράμμων τμημάτων αν δίνονται τα άκρα τους από Ροδόλφο Μπόρη
εύρεση του κέντρου κύκλου μόνο με το διαβήτη από Μπάμπη Στεργίου
κατασκευή μόνο με διαβήτη της καθέτου σε ευθύγραμμο τμήμα στις πλευρές τετραγώνου στο οποίο βαίνει γωνία
 με κορυφή την απέναντι κορυφή του τετραγώνου
με κορυφή την απέναντι κορυφή του τετραγώνουκατασκευή από σημείο Α, που δεν ευρίσκεται επί ευθείας ε, κάθετης σε αυτήν χρησιμοποιώντας μόνο μία φορά κύκλο (ή τμήμα κύκλου) και χρησιμοποιώντας όσες ευθείες χρειάζεστε από Σωτήρη Λουρίδα
κατασκευή από σημείο Α, που ευρίσκεται επί ευθείας ε, κάθετης σε αυτήν χρησιμοποιώντας μόνο 2 φορές κύκλο (ή τμήμα κύκλου) και χρησιμοποιώντας όσες ευθείες χρειάζεστε από Σωτήρη Λουρίδα
κατασκευή ευθείας που ενώνει δυο σημεία μόνο με κανόνα μικρότερης απόστασης από την απόσταση των σημείων από dimitris pap
έχουμε ευθεία (ε) και σημείο A εκτός αυτής.Χρησιμοποιώντας μόνο μία φορά τον διαβήτη και όσες θέλουμε τον κανόνα, να βρεθούν κατασκευαστικά τρία σημεία, έστω K,B,C με τα B,C να ανήκουν στην (ε), ώστε να είμαστε σίγουροι ότι οι περιγεγραμμένοι κύκλοι στά τρίγωνα
 είναι ίσοι. από Σωτήρη Λουρίδα
είναι ίσοι. από Σωτήρη ΛουρίδαΤμημάτων Μήκους
 από Σωτήρη Λουρίδα
από Σωτήρη Λουρίδα![\sqrt[4]{{\alpha ^4 + \beta ^4 }} \sqrt[4]{{\alpha ^4 + \beta ^4 }}](/forum/ext/geomar/texintegr/latexrender/pictures/b8b0c917bffaf1738c1f2ee745728143.png) από Σωτήρη Λουρίδα
από Σωτήρη Λουρίδα , πχ,
, πχ,  από smarpant
από smarpant  από Γιώργο Ρίζο
από Γιώργο Ρίζο αν έχουμε σαν δεδομένα δύο ευθύγραμμα τμήματα με μήκη
αν έχουμε σαν δεδομένα δύο ευθύγραμμα τμήματα με μήκη  , με την ιδιότητα
, με την ιδιότητα  από Σωτήρη Λουρίδα
από Σωτήρη Λουρίδα από Φωτεινή Καλδη
από Φωτεινή Καλδη από Φωτεινή Καλδη
από Φωτεινή Καλδη από Φωτεινή Καλδη
από Φωτεινή Καλδη από Φωτεινή Καλδη
από Φωτεινή Καλδη από Atemlos
από AtemlosΑσυνήθιστες
χωρισμός αμβλυγωνίου τριγώνου ΑΒΓ σε μη επικαλυπτόμενα οξυγώνια τρίγωνα (δεν υπάρχει περιορισμός στο πλήθος και στην θέση) από Σεραφείμ Τσιπέλη
έχουμε ένα τετράδιο με τουλάχιστον δύο φύλλα και ένα μολύβι. Σχίζουμε το ένα φύλλο του τετραδίου.Να βρείτε (σημαδέψετε με το μολύβι) το μέσον της μικρότερης πλευράς του φύλλου (ορθογωνίου) που σχίσατε. Σημείωση: Δεν επιτρέπεται η δίπλωση του φύλλου και δεν μπορεί να χρησιμοποιηθεί κανένα άλλο αντικείμενο πλην αυτών που αναφέρονται στο πρόβλημα από Παναγιώτη Γιαννόπουλο
ένας γεωμέτρης διαθέτει ένα όργανο με το οποίο μπορεί να χαράσσει :
α) μία ευθεία που να διέρχεται από δύο δοσμένα σημεία και β) μία ευθεία κάθετη προς δοσμένη ευθεία σε δοσμένο σημείο της.
Πως θα μπορέσει ο γεωμέτρης με τη βοήθεια αυτού του οργάνου να φέρει από ένα σημείο εκτός ευθείας κάθετη προς την ευθεία αυτή; από Φωτεινή Καλδη
δίνεται τρίγωνο ΔΕΖ.Να προσδιορίσετε το πλήθος των κατασκευάσιμων τριγώνων ΑΒΓ με Δ,Ε,Ζ εσωτερικά σημεία αντίστοιχα των πλευρών ΒΓ,ΓΑ,ΑΒ, γωνΑ=2γωνΓ (<Α=2<Γ) και με την πλευρά ΑΓ ίση με δοθέν ευθύγραμμο τμήμα,έστω λ από Σωτήρη Λουρίδα
κατασκευή τετραπλεύρου με συναρμολόγηση τριγώνων από dimplak (νδο τα τρίγωνα ΑΚΝ, ΒΚΛ, ΓΛΜ και ΔΜΝ μπορούν να συναρμολογηθούν με τρόπο ώστε να προκύψει το τετράπλευρο ΚΛΜΝ όπου τα Κ,Λ,Μ και Ν είναι τα μέσα των πλευρών του κυρτού τετραπλεύρου ΑΒΓΔ)
δίνεται ευθεία (ε) και σημείο Α εκτός αυτής. Θεωρούμε γωνία xΑy σταθερού μέτρου περιστρεφόμενη περί το Α και που οι πλευρές της στην τυχούσα θέση τέμνουν την (ε) στα σημεία Β, Γ. Να βρεθεί, κατασκευαστικά,
1) H θέση που το ευθύγραμμο τμήμα ΒΓ θα ισούται με δοθέν ευθύγραμμο τμήμα.
2) H θέση που το ευθύγραμμο τμήμα ΒΓ είναι ελάχιστο.
3) Η θέση που το γινόμενο (ΑΒ)(ΒΓ), να είναι δοθέν από Σωτήρη Λουρίδα
Ισεμβαδικά - ισοπεριμετρικά
εύρεση θέση του τμήματος με ελάχιστο μήκος σε ισοσκελές και ορθογώνιο τρίγωνο ώστε να το χωρίζει σε 2 ισεμβαδικά τρίγωνα από Παναγιώτη Γκριμπαβιώτη
διαίρεση τριγώνου σε ισεμβαδικά χωρία με ευθεία διερχόμενη από σημείο πλευράς τριγώνου από Νίκο Ζαφειρόπουλο
διαίρεση τρίγωνου σε ισεμβαδικά χωρία με ευθεία διερχόμενη από σημείο εκτός τριγώνου από Νίκο Ζαφειρόπουλο
διαίρεση τρίγωνου σε ισεμβαδικά και ισοπεριμετρικά χωρία με ευθεία (εξισωτής τριγώνου)
διαίρεση τρίγωνου σε 2 χωρία με σταθερό λόγο περιμέτρων με ευθεία από Σωτήρη Λουρίδα
διαίρεση ισοσκελούς τρίγωνου σε δυο ισοσκελή τρίγωνα με ευθεία από κορυφή του από Γιώργο Απόκη
διαίρεση μέρους ορθογωνίου εκτός κύκλου σε δύο ισεμβαδικά χωρία με ευθεία (δοθέντος κύκλου εντός ορθογωνίου) από miltos
διαίρεση μέρους ορθογωνίου εκτός άλλου ορθογωνίου σε δύο ισεμβαδικά χωρία με ευθεία (δοθέντος ορθογωνίου εντός ορθογωνίου) από Παναγιώτη Γιαννόπουλο
διαίρεση τριγώνου σε ισοπεριμετρικά σχήματα με ευθείας από το μέσο πλευράς σκαληνού τριγώνου από komi
διαίρεση κυρτού τετράπλευρου σε τρία ισοδύναμα (ίσων εμβαδών) μέρη με ευθείες που να διέρχονται από δοθέν σημείο μιας πλευράς του από Σωτήρη Λουρίδα
εγγραφή τριγώνου με ελάχιστο λόγο εμβαδών από Ανδρέα Βαρβεράκη (δίδεται ορθογώνιο και ισοσκελές τρίγωνο
 . Να εγγραφεί σε αυτό, άλλο ορθογώνιο και ισοσκελές τρίγωνο (οι κορυφές του να ανήκουν ανά μία στις πλευρές του αρχικού), τέτοιο ώστε ο λόγος του εμβαδού του προς εκείνο του αρχικού, να είναι ελάχιστος.)
. Να εγγραφεί σε αυτό, άλλο ορθογώνιο και ισοσκελές τρίγωνο (οι κορυφές του να ανήκουν ανά μία στις πλευρές του αρχικού), τέτοιο ώστε ο λόγος του εμβαδού του προς εκείνο του αρχικού, να είναι ελάχιστος.)Εύρεση σημείων
ύπαρξη ευθείας από Σωτήρη Λουρίδα (δίνεται γωνία
 σημείο Ρ εσωτερικό της και σημείο Σ στο εσωτερικό της παραπληρωματικής της
σημείο Ρ εσωτερικό της και σημείο Σ στο εσωτερικό της παραπληρωματικής της  (Οη,Οy εκατέροθεν της ευθείας Οx). νδο υπάρχει ευθεία διερχόμενη από το σημείο Σ που να τέμνει τις Οx,Οy σε σημεία Α, Β αντίστοιχα ώστε τα σημεία Ο, Α, Ρ, Β να είναι σημεία του ίδιου κύκλου. Είναι δυνατόν να οριστεί ,κατασκευαστικά, η ευθεία αυτή; )
(Οη,Οy εκατέροθεν της ευθείας Οx). νδο υπάρχει ευθεία διερχόμενη από το σημείο Σ που να τέμνει τις Οx,Οy σε σημεία Α, Β αντίστοιχα ώστε τα σημεία Ο, Α, Ρ, Β να είναι σημεία του ίδιου κύκλου. Είναι δυνατόν να οριστεί ,κατασκευαστικά, η ευθεία αυτή; )ύπαρξη 2 ευθειών από Σωτήρη Λουρίδα (δίνεται γωνία
 σημείο Ρ εσωτερικό της και σημείο Σ στο εσωτερικό της παραπληρωματικής της
σημείο Ρ εσωτερικό της και σημείο Σ στο εσωτερικό της παραπληρωματικής της (Οη,Οy εκατέρωθεν της ευθείας Οx). νδο υπάρχουν δύο ευθείες (μή ταυτιζόμενες) διερχόμενες από το σημείο Σ που να τέμνουν η πρώτη τις Οx,Οy σε σημεία Α, Β αντίστοιχα και η δεύτερη επίσης τις Οx,Οy στα σημεία Γ, Δ αντίστοιχα ώστε
(Οη,Οy εκατέρωθεν της ευθείας Οx). νδο υπάρχουν δύο ευθείες (μή ταυτιζόμενες) διερχόμενες από το σημείο Σ που να τέμνουν η πρώτη τις Οx,Οy σε σημεία Α, Β αντίστοιχα και η δεύτερη επίσης τις Οx,Οy στα σημεία Γ, Δ αντίστοιχα ώστε  Είναι δυνατόν να οριστούν ,κατασκευαστικά, οι ευθείες αυτές;)
Είναι δυνατόν να οριστούν ,κατασκευαστικά, οι ευθείες αυτές;)εύρεση σημείου από Σωτήρη Λουρίδα (έστω γωνία xOy και δύο σημεία Α, Β στο εσωτερικό της. Είναι δυνατόν να προσδιοριστεί (κατασκευαστικά) σημείο C της Οx ώστε :
 όταν
όταν  )
)εύρεση σημείου από KARKAR (δίνεται κύκλος
 με τα σταθερά , αντιδιαμετρικά σημεία του
με τα σταθερά , αντιδιαμετρικά σημεία του  , και ευθεία
, και ευθεία  , με το σταθερό της σημείο
, με το σταθερό της σημείο  . Να βρεθεί σημείο
. Να βρεθεί σημείο  , επί του κύκλου , ώστε αν οι
, επί του κύκλου , ώστε αν οι  , τέμνουν την ευθεία
, τέμνουν την ευθεία  στα σημεία
στα σημεία  αντίστοιχα , το
αντίστοιχα , το  να είναι το μέσο του
να είναι το μέσο του  )
)εύρεση σημείου από Σωτήρη Λουρίδα (δίνεται ευθεία ΧΟΨ και δύο σημεία Α, Β μή ανήκοντα σε αυτή.Να προσδιοριστεί κατασκευαστικά σημείο Μ της (ε) ώστε <ΧΜΑ = 2<ΨΜΒ.)
εύρεση σημείου από KARKAR (να βρεθεί ( κατασκευασθεί ) σημείο S πάνω στον περίκυκλο τριγώνου
 , ώστε για κάθε κύκλο που διέρχεται από τα
, ώστε για κάθε κύκλο που διέρχεται από τα  , και τέμνει τις πλευρές
, και τέμνει τις πλευρές  στα σημεία D , E αντίστοιχα , να προκύπτει :
στα σημεία D , E αντίστοιχα , να προκύπτει :  )
)εύρεση σημείου από KARKAR (Στο "άνω" ημικύκλιο , κύκλου διαμέτρου
 , βρίσκονται τα σημεία
, βρίσκονται τα σημεία  και
και  . Βρείτε τη θέση σημείου S στο "κάτω" ημικύκλιο , ώστε οι
. Βρείτε τη θέση σημείου S στο "κάτω" ημικύκλιο , ώστε οι  να τέμνουν τη διάμετρο σε σημεία
να τέμνουν τη διάμετρο σε σημεία  , συμμετρικά ως προς το κέντρο
, συμμετρικά ως προς το κέντρο  )
)εύρεση σημείου από Σωτήρη Λουρίδα (δίνεται κύκλος
 και δύο σημεία του επιπέδου του
και δύο σημεία του επιπέδου του  που δεν ανήκουν σε αυτόν. Εξετάστε αν δύναται να προσδιοριστεί κατασκευαστικά σημείο
που δεν ανήκουν σε αυτόν. Εξετάστε αν δύναται να προσδιοριστεί κατασκευαστικά σημείο  του κύκλου, ώστε να ισχύει
του κύκλου, ώστε να ισχύει  , όπου
, όπου  οι τομές των
οι τομές των  με τον δοθέντα κύκλο ,
με τον δοθέντα κύκλο ,  οι αντίστοιχοι διάμεσοι των τριγώνων
οι αντίστοιχοι διάμεσοι των τριγώνων  που άγονται από την κοινή κορυφή τους
που άγονται από την κοινή κορυφή τους  και
και  οι αντίστοιχοι εσωτερικοί διχοτόμοι των γωνιών των ίδιων τριγώνων που επίσης άγονται από την κοινή κορυφή τους
οι αντίστοιχοι εσωτερικοί διχοτόμοι των γωνιών των ίδιων τριγώνων που επίσης άγονται από την κοινή κορυφή τους  )
)εύρεση σημείου από KARKAR (2 ευθείες
 και
και 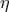 , τέμνονται στο
, τέμνονται στο  και έστω σημείο
και έστω σημείο  της
της  και σημείο
και σημείο  της
της 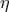 .Να κατασκευασθεί σημείο
.Να κατασκευασθεί σημείο  της
της  , ώστε αν
, ώστε αν  το συμμετρικό του ως προς
το συμμετρικό του ως προς  , η
, η  να είναι διχοτόμος της
να είναι διχοτόμος της 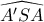 )
)εύρεση 2 σημείων από Σωτήρη Λουρίδα (σε τρίγωνο ΑΒΓ να κατασκευαστούν δύο σημεία Δ της ΑΒ και Ε της ΑΓ ώστε το ΒΔ+ΔΕ+ΕΓ είναι δεδομένο όπως επίσης είναι δεδομένο και το εμβαδόν (ΒΔΕΓ) του τετραπλεύρου ΒΔΕΓ)
εύρεση 2 σημείων από Σωτήρη Λουρίδα (δίνεται γωνία xOy και δύο σημεία των πλευρών της A,B αντίστοιχα των Οχ, Οψ διάφορα του Ο.Υπάρχει ευθύγραμμο τμήμα KL με K σημείο της Οx και L σημείο της Οy, ώστε (KL^2-KA^2=c^2) και (KL^2-KB^2=t^2), όταν c,t δοθείσες θετικές σταθερές; Είναι δυνατή (αν υπάρχει) η κατασκευή του KL;)
εύρεση 2 σημείων από KARKAR (έστω τρίγωνο
 , αμβλυγώνιο στο
, αμβλυγώνιο στο  . Βρείτε δύο σημεία
. Βρείτε δύο σημεία  στη βάση
στη βάση  , τέτοια ώστε :
, τέτοια ώστε :  και
και  . Στη συνέχεια δείξτε ότι :
. Στη συνέχεια δείξτε ότι :  )
)εύρεση 2 σημείων από Σωτήρη Λουρίδα (δίνονται στο επίπεδο τρία σημεία, όχι κατ’ ανάγκη της ίδιας ευθείας,
 Θεωρούμε τους κύκλους με διαμέτρους τα
Θεωρούμε τους κύκλους με διαμέτρους τα  Ζητάμε την κατασκευή δύο αντίστοιχων σημείων
Ζητάμε την κατασκευή δύο αντίστοιχων σημείων  στούς κύκλους και με την σειρά που τούς αναφέραμε, ώστε:
στούς κύκλους και με την σειρά που τούς αναφέραμε, ώστε:  με
με  να είναι δοθέντα ευθύγραμμα τμήματα.)
να είναι δοθέντα ευθύγραμμα τμήματα.)εύρεση 2 σημείων από Σωτήρη Λουρίδα (θεωρούμε ορθή γωνία <xOy= 9
 . Έστω δύο κινούμενα σημεία
. Έστω δύο κινούμενα σημεία  ώστε η ευθεία ΑΒ να εφάπτεται σε δοθέντα κύκλο (O, R) και σε αντίστοιχο σημείο του, έστω Γ. Να αιτιολογήσετε σε ποια θέση της ΑΒ το άθροισμα
ώστε η ευθεία ΑΒ να εφάπτεται σε δοθέντα κύκλο (O, R) και σε αντίστοιχο σημείο του, έστω Γ. Να αιτιολογήσετε σε ποια θέση της ΑΒ το άθροισμα  γίνεται ελάχιστο, όταν k, m δοθέντες θετικοί αριθμοί.)
γίνεται ελάχιστο, όταν k, m δοθέντες θετικοί αριθμοί.)εύρεση 2 σημείων (θεωρούμε γωνία
 και δύο σημεία
και δύο σημεία  κινούμενα στις πλευρές
κινούμενα στις πλευρές  αντίστοιχα ώστε να διατηρείται το μήκος
αντίστοιχα ώστε να διατηρείται το μήκος  .
. Έστω
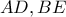 οι δύο διχοτόμοι του τριγώνου
οι δύο διχοτόμοι του τριγώνου  .
.Προσδιορίστε (με απόδειξη) την θέση του
 , ώστε το γινόμενο
, ώστε το γινόμενο  να παίρνει την μέγιστη τιμή.)
να παίρνει την μέγιστη τιμή.)εύρεση 2 σημείων από Ανδρέα Βαρβεράκη (ευθύγραμμου τμήματος ΔΕ με τα σημεία Δ, Ε να ανήκουν στις πλευρές ΑΒ,ΑΓ αντίστοιχα, τυχαίου τριγώνου ΑΒΓ τέτοιο ώστε ΒΔ=ΔΕ=ΕΓ)
εύρεση 2 σημείων από Δημήτρη Σκουτέρη (ευθύγραμμου τμήματος δεδομένου μήκους και παράλληλου σε δεδομένη ευθεία , του οποίου τα άκρα να βρίσκονται επί δεδομένων κύκλων)
εύρεση 2 σημείων από KARKAR (ισόπλευρο τρίγωνο
 , είναι τοποθετημένο μεταξύ δύο παραλλήλων ευθειών.Να κατασκευασθεί τμήμα DH , με άκρα επί των ευθειών , το οποίο να τριχοτομείται από τα σημεία τομής του E , Z , με τις δύο πλευρές του τριγώνου )
, είναι τοποθετημένο μεταξύ δύο παραλλήλων ευθειών.Να κατασκευασθεί τμήμα DH , με άκρα επί των ευθειών , το οποίο να τριχοτομείται από τα σημεία τομής του E , Z , με τις δύο πλευρές του τριγώνου )εύρεση 2 σημείων από petros r (βρείτε την μικρότερη τιμή του x τέτοια ώστε, για οποιαδήποτε σημείο Α μέσα σε ισόπλευρο τρίγωνο με πλευρά 1, μπορούμε πάντα να διαλέξουμε δύο σημεία στις πλευρές του τριγώνου που βρίσκονται στην ίδια ευθεία με το Α και έχουν απόσταση x μεταξύ τους.)
Κατασκευές ευθείας
διχοτόμου μιας γωνίας της οποίας η κορυφή βρίσκεται έξω από το φύλλο σχεδίασης από Μάκη Χατζόπουλο (κι εδώ , εδώ)
κοινό εφαπτόμενο τμήμα 2 (εφαπτόμενων) ημικυκλίων από KARKAR
κοινών εξωτερικών εφαπτομένων 2 κύκλων από dimitris pap
ευθείας διερχόμενη από σημείο ώστε να σχηματίζει ισόπλευρο τρίγωνο με δοσμένες παράλληλες ευθείες και άλλο σημείο από KARKAR (σημείο
 βρίσκεται μέσα στη ζώνη των παραλλήλων ευθειών
βρίσκεται μέσα στη ζώνη των παραλλήλων ευθειών  , και σημείο
, και σημείο  επί της
επί της  Να αχθεί τρίτη ευθεία , η οποία να διέρχεται από το
Να αχθεί τρίτη ευθεία , η οποία να διέρχεται από το  , έτσι ώστε αν τέμνει τις ευθείες
, έτσι ώστε αν τέμνει τις ευθείες  στα
στα  το τρίγωνο
το τρίγωνο  , να είναι ισοσκελές)
, να είναι ισοσκελές)ευθείας (μεταβλητής παράλληλης προς τις βάσεις τραπεζίου) από Κώστα Βήττα (ευθεία
 παράλληλη προς τις βάσεις
παράλληλη προς τις βάσεις  δοσμένου τραπεζίου
δοσμένου τραπεζίου  τέμνει τις πλευρές του
τέμνει τις πλευρές του  στα σημεία
στα σημεία  αντιστοίχως και έστω τα σημεία
αντιστοίχως και έστω τα σημεία  και
και  Προσδιορίστε τη θέση της
Προσδιορίστε τη θέση της  ώστε το
ώστε το  να είναι παραλληλόγραμμο.)
να είναι παραλληλόγραμμο.)ευθείας παράλληλης στη ΒΓ σε τρίγωνο ΑΒΓ, η οποία να τέμνει την ΑΒ στο Δ και την ΑΓ στο Ε και να είναι ΔΜΕ=90 μοίρες, όπου Μ το μέσο της ΒΓ από dimplak
τέμνουσας σε γωνία από Γιώργο Απόκη (δίνεται γωνία
 ,
,  εσωτερικό σημείο της και πραγματική σταθερά
εσωτερικό σημείο της και πραγματική σταθερά  . Να κατασκευαστεί ευθεία που να διέρχεται από το
. Να κατασκευαστεί ευθεία που να διέρχεται από το  και να τέμνει τις πλευρές της γωνίας στα
και να τέμνει τις πλευρές της γωνίας στα  , έτσι ώστε α)
, έτσι ώστε α)  β) το
β) το  να είναι ελάχιστο.)
να είναι ελάχιστο.)Λοιπές κατασκευές
έγκεντρου, διαμέσων, βαρύκεντρου, ορθόκεντρου, περίκεντρου,ύψών σε τρίγωνο, του οποίου οι κορυφές βρίσκονται έξω από το χαρτί σχεδιάσεως από Νίκο Κυριαζή
Κατασκευή τριγώνου
ισοπλεύρου τριγώνου εγγεγραμμένου σε τετράγωνο από Ανδρέα Πούλο
τριγώνου ΑΒΓ από την πλευρά του ΒΓ=α, τη διάμεσό του ΑΜ=μ και τη διαφορά των γωνιών του Β και Γ, Β-Γ=φ από ypatia
τριγώνου ΑΒΓ από την πλευρά του ΒΓ=α και γνωστής θέσης, την ευθεία ε, επί της οποίας βρίσκεται η κορυφή Α και τη διαφορά των γωνιών του Β και Γ, Β-Γ=φ από ypatia
τριγώνου ΑΒΓ από την πλευρά του ΒΓ=α, τη διαφορά των γωνιών του Β και Γ, Β-Γ=φ και το γινόμενο των πλευρών του ΑΒ * ΑΓ = λ^2 από ypatia
τριγώνου ΑΒΓ από την πλευρά του ΒΓ=α, τη διαφορά των γωνιών του Β-Γ=φ και τον πόδα Δ επί την ΒΓ του ύψους ΑΔ από ypatia
τριγώνου με δεδομένη την ακτίνα του περιγεγραμμένου κύκλου (
 ), το άθροισμα δυο πλευρών (
), το άθροισμα δυο πλευρών (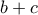 ) και τη διαφορά των αντίστοιχων γωνιών (
) και τη διαφορά των αντίστοιχων γωνιών ( ) από Δημήτρη Σκουτέρη
) από Δημήτρη Σκουτέρητριγώνου με πλευρές
 και ακτίνα περιγεγραμμένου κύκλου
και ακτίνα περιγεγραμμένου κύκλου  όταν είναι γνωστά τα
όταν είναι γνωστά τα  και
και  από Δημήτρη Σκουτέρη
από Δημήτρη Σκουτέρητριγώνου ΑΒΓ αν είναι γνωστά τα μήκη των υψών από τα Α,Β και της διαμέσου από το Α από Φωτεινή Καλδη
τριγώνου ΑΒΓ όταν δίνονται η γωνία Α,το άθροισμα ΑΒ+ΑΓ,το εμβαδόν του (ΑΒΓ) από Σωτήρη Λουρίδα
τριγώνου ΑΒΓ, το οποίο είναι όμοιο σε τρίγωνο με κορυφές επι τριών γνωστών ομόκεντρων κύκλων από antegeia
τριγώνου ABC όταν δίνονται η ακτίνα του περιγραμμένου κύκλου του, η περίμετρος του και ότι το τρίγωνο ABC είναι τέτοιο πού ο περιγεγραμμένος κύκλος του τριγώνου
 , που είναι ομοιόθετο του ABC στην ομοιοθεσία
, που είναι ομοιόθετο του ABC στην ομοιοθεσία  όπου t δεδομένος θετικός αριθμός, να εφάπτεται της BC από Σωτήρη Λουρίδα
όπου t δεδομένος θετικός αριθμός, να εφάπτεται της BC από Σωτήρη Λουρίδατριγώνου ΑΒΓ, όταν δίνονται το εμβαδόν του, η γωνία του
 και ένα σημείο
και ένα σημείο  που δεν ανήκει στις πλευρές Ax, Ay αλλά ανήκει στην ευθεία ΒΓ από Σωτήρη Λουρίδα
που δεν ανήκει στις πλευρές Ax, Ay αλλά ανήκει στην ευθεία ΒΓ από Σωτήρη Λουρίδατριγώνου ΑΒΓ όταν δίνονται τα σημεία Δ, Ε, Ζ όταν Δ είναι το ίχνος της διχοτόμου ΑΔ, Ε είναι το μέσον της πλευράς ΑΓ και Ζ το σημείο τομής της ΓΛ με την πλευρά ΑΒ, όπου Λ το σημείο τομής των ΑΔ ,ΒΕ από Σωτήρη Λουρίδα
τριγώνου αν δίνονται το μέγεθος kβγ/λR (β,γ πλευρές, R η ακτίνα του περιγεγραμμένου κύκλου),με κ,λ δοθείσες θετικές σταθερές,η διαφορά των γωνιών Β-Γ, η ισχύς της ισότητας β+γ=nα (οταν α η τρίτη πλευρά), όπου n δοθεντας θετικός ακέραιος από Σωτήρη Λουρίδα
τριγώνου ΑΒΓ εαν ΒΓ = 8, γωνία ΒΓΑ = 120 μοίρες και η διάμεσος ΓΔ είναι κάθετη στην πλευρά ΒΓ από Ανδρέα Πούλο
τριγώνου
 αν είναι γνωστά τα ύψη του
αν είναι γνωστά τα ύψη του  και η διάμεσός του
και η διάμεσός του  από Φωτεινή Καλδη
από Φωτεινή Καλδητριγώνου δοθέντος ισοπλεύρου τριγώνου από Στάθη Κούτρα (δίνεται ισόπλευρο τρίγωνο ΑΒΓ και σημείο Ο στο εσωτερικό του που δεν ανήκει στον περιγεγραμμένο κύκλο του τριγώνου ΑΒΓ. Να δειχθεί ότι με πλευρές τις ΟΑ, ΟΒ, ΟΓ κατασκευάζεται πάντοτε τρίγωνο και οι γωνίες του είναι
 . Τι συμβαίνει όταν το Ο είναι εξωτερικό του τριγώνου;)
. Τι συμβαίνει όταν το Ο είναι εξωτερικό του τριγώνου;)τριγώνου ΑΒΓ με Α εσωτερικό σημείο γωνίας xOy ,
 και με επιπλέον δεδομένα, την γωνία
και με επιπλέον δεδομένα, την γωνία  και το γινόμενο
και το γινόμενο  (ω, k>0 δεδομένα μεγέθη) από Σωτήρη Λουρίδα
(ω, k>0 δεδομένα μεγέθη) από Σωτήρη Λουρίδατριγώνου εφαπτόμενου σε 3 σταθερούς κύκλους από Σωτήρη Λουρίδα (είναι δυνατόν να υπάρχουν τρείς σταθεροί κύκλοι (Κ,ρ), (Λ,σ), (Μ,τ) και ένα τρίγωνο ΑΒΓ που οι πλευρές του ΑΒ, ΑΓ, ΒΓ να εφάπτονται αντίστοιχα στους κύκλους αυτούς και να συνεχίζουν να εφάπτονται με την ίδια αντιστοιχία για άπειρες θέσεις του ίδιου τριγώνου; )
ισοσκελούς τριγώνου από Κώστα Βήττα (να κατασκευαστεί ισοσκελές τρίγωνο
 με
με  αν δίνονται η κορυφή του
αν δίνονται η κορυφή του  η ευθεία
η ευθεία  τυχόν σημείο
τυχόν σημείο  στην προέκταση της πλευράς
στην προέκταση της πλευράς  προς το μέρος του
προς το μέρος του  και τυχόν κύκλος
και τυχόν κύκλος  χορδής
χορδής  με το κέντρο του
με το κέντρο του  προς το μέρος της
προς το μέρος της  που δεν κείνται το
που δεν κείνται το  )
)τριγώνου με δεδομένο το περίκεντρο
 , το έγκεντρο
, το έγκεντρο  και ένα παράκεντρο
και ένα παράκεντρο  . από Δημήτρη Σκουτέρη
. από Δημήτρη Σκουτέρητριγώνου που ορίζουν τα μέσα ευθυγράμμων τμημάτων αγόμενα από τις κορυφές του από Παναγιώτη Γιαννόπουλο
τριγώνου
 με πλευρές
με πλευρές  αν γνωρίζουμε τα μήκη των
αν γνωρίζουμε τα μήκη των  απόthemiskant
απόthemiskantτριγώνου
 όταν δίνονται
όταν δίνονται  , το ύψος
, το ύψος  , όταν
, όταν  δοθέντα ευθύγραμμα τμήματα και ότι η εσωτερική διχοτόμος του τριγώνου αυτού είναι μέση ανάλογη των τμημάτων που ορίζει αυτή επί της βάσης
δοθέντα ευθύγραμμα τμήματα και ότι η εσωτερική διχοτόμος του τριγώνου αυτού είναι μέση ανάλογη των τμημάτων που ορίζει αυτή επί της βάσης  από Σωτήρη Λουρίδα
από Σωτήρη Λουρίδατριγώνου
 αν δίνονται η γωνία του
αν δίνονται η γωνία του  , το ύψος του
, το ύψος του  και το
και το  ,όπου τ η ημιπερίμετρος του. από Άλκη Μπεντεβή
,όπου τ η ημιπερίμετρος του. από Άλκη Μπεντεβήτριγώνου
 , αν δίνονται: η πλευρά του
, αν δίνονται: η πλευρά του  , η ακτίνα
, η ακτίνα  του περιγεγραμμένου του κύκλου (
του περιγεγραμμένου του κύκλου ( ) και η διαφορά
) και η διαφορά  , όπου
, όπου  και
και  . από Βαγγέλη Μουρούκο
. από Βαγγέλη Μουρούκοτριγώνου
 αν δίνονται:
αν δίνονται:  Με
Με  το ύψος του και διχοτόμος του αντίστοιχα που άγονται από την κορυφή του
το ύψος του και διχοτόμος του αντίστοιχα που άγονται από την κορυφή του  . από Σωτήρη Λουρίδα
. από Σωτήρη Λουρίδαισοσκελούς τριγώνου από Κώστα Βήττα (δίνεται τρίγωνο
 και έστω
και έστω 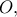 τυχόν σημείο στο εσωτερικό του. Ζητείται να προσδιοριστούν τα σημεία
τυχόν σημείο στο εσωτερικό του. Ζητείται να προσδιοριστούν τα σημεία 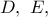 επί των
επί των  αντιστοίχως, ώστε το τρίγωνο
αντιστοίχως, ώστε το τρίγωνο  να είναι ισοσκελές με
να είναι ισοσκελές με  και
και  όπου
όπου  είναι δοσμένη γωνία)
είναι δοσμένη γωνία)τριγώνου όταν γνωρίζουμε τις ακτίνες του εγγεγραμμένου και του περιγεγραμμένου κύκλων του από Σωτήρη Λουρίδα
Κατασκευή τετραπλεύρου
τραπέζιου
 όταν δίνονται οι πλευρές ΑΔ=α, ΒΓ=β και οι διαγώνιες ΒΔ=γ, ΑΓ=δ
όταν δίνονται οι πλευρές ΑΔ=α, ΒΓ=β και οι διαγώνιες ΒΔ=γ, ΑΓ=δ  από Σωτήρη Λουρίδα
από Σωτήρη Λουρίδακοινής εξωτερικής εφαπτομένης δύο κύκλων με διάκεντρο μεγαλύτερη της διαφοράς των δύο ακτίνων από Σπύρο Καρδαμίτση
τετραγώνου εγγεγραμμένου σε τρίγωνο από Ανδρέα Πούλο
κυρτού τετραπλεύρου
 , όταν δίνονται τα στοιχεία του:
, όταν δίνονται τα στοιχεία του:  όταν
όταν  δεδομένα ευθύγραμμα τμήματα από Σωτήρη Λουρίδα
δεδομένα ευθύγραμμα τμήματα από Σωτήρη Λουρίδαεγγράψιμου κυρτού τετράπλευρου από Σωτήρη Λουρίδα (δίνεται κυρτό τετράπλευρο
 με
με  .Αποδείξτε την κατασκευαστική ύπαρξη εγγράψιμου κυρτού τετραπλεύρου
.Αποδείξτε την κατασκευαστική ύπαρξη εγγράψιμου κυρτού τετραπλεύρου  με τις ίδιες κατά σειρά πλευρές
με τις ίδιες κατά σειρά πλευρές  .)
.)αμφιγράψιμου τετραπλεύρου από Grigoris K. (Εις δοθέντα κύκλον να εγγραφή τετράπλευρον
 του οποίου δίδεται η διαγώνιος
του οποίου δίδεται η διαγώνιος  , η γωνία των διαγωνίων και το οποίον να είναι συγχρόνως και περιγράψιμον εις κύκλον.)
, η γωνία των διαγωνίων και το οποίον να είναι συγχρόνως και περιγράψιμον εις κύκλον.)Κατασκευή ν-γωνου με 5+ πλευρές
μη κανονικόυ εξάγωνου ΑΒΓΔΕΖ με ίσες πλευρές τέτοιο ώστε οι πλευρές ΑΒ, ΓΔ και ΕΖ τα βρίσκονται πάνω στις πλευρές ισοπλεύρου τριγώνου ΚΛΜ από Ανδρέα Βαρβεράκη
Κατασκευή κύκλου
κύκλου εφαπτόμενου σε κύκλο και σε ευθεία σε δοθέν σημείο αυτής από Κώστα Σερίφη
κύκλου εφαπτόμενου σε 2 εξωτερικά εφαπτόμενους κύκλους και στην κοινή εφαπτομένη τους από Κώστα Βήττα
κύκλου διερχόμενου από σταθερό σημείο κι εφαπτόμενου σε ευθεία και σε κύκλο από Φωτεινή Καλδη
κύκλου εφαπτόμενου σε κύκλου και διερχόμενου από 2 σημεία εκτός κύκλου από papel
κύκλου εφαπτόμενου σε ευθεία και διερχόμενου από 2 σημεία εκτός ευθείας από papel
κύκλου που εφάπτεται εσωτερικά στον περιγεγραμμένο κύκλο τριγώνου και σε δύο πλευρές του από Σωτήρη Λουρίδα
κύκλου εφαπτόμενου σε ευθεία και κύκλο από geomyljason
κύκλου που να διέρχεται από σημείο και να εφάπτεται σε 2 ευθείες από Φωτεινή Καλδη
κύκλου
 ώστε να διέρχεται από την κορυφή
ώστε να διέρχεται από την κορυφή  και να εφάπτεται στις πλευρές
και να εφάπτεται στις πλευρές  και
και  σε τετράγωνο
σε τετράγωνο  από Κώστα Δόρτσιο
από Κώστα Δόρτσιοκύκλου διερχόμενου από δυο δοθέντα σημεία που να τέμνει δοθείσα ευθεία κατά χορδή που να απέχει από το κέντρο του δοθείσα απόσταση από Σωτήρη Λουρίδα
Αδύνατες
εύρεση σημείου από Σωτήρη Λουρίδα (θεωρούμε κύκλο C, χορδή του ΒΓ και σημείο Δ της χορδής αυτής διάφορο των άκρων της. Να προσδιοριστεί σημείο Α της μεσοκάθετης της ΒΓ ώστε αν Ε η τομή της ΑΔ με το μεγάλο τόξο ΒΓ, να έχουμε:
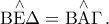 )
)πρόβλημα νεύσης από Σωτήρη Λουρίδα (δίνεται κυρτή γωνία <xOy και σημείο Α της παραπληρωματικής της μη ανήκον στις ημιευθείες Ox, Oy.Να εξεταστεί αν μπορεί, εν γένει, να κατασκευαστεί ευθεία διερχόμενη από το Α και τέμνουσα τις Ox, Oy στά σημεία Β, Γ, ώστε το ΒΓ να ισούται με δεδομένο ευθύγραμμο τμήμα,)
ευθείας διερχόμενης από την κορυφή Δ ορθογωνίου ΑΒΓΔ, η οποία να τέμνει τις ευθείες ΑΒ, ΒΓ στα Κ, Λ αντίστοιχα, ώστε ΟΚ=ΟΛ, όπου Ο το κέντρο του ορθογωνίου
κατασκευή ευθείας από Atemlos
(οι ευθείες
 και
και  είναι παράλληλες και οι
είναι παράλληλες και οι  και
και  κάθετες.Εαν
κάθετες.Εαν  τότε να δείξετε ότι η γωνία
τότε να δείξετε ότι η γωνία  είναι διπλάσια της γωνίας
είναι διπλάσια της γωνίας  )
)κατασκευή τριγώνου από Doloros (τριγώνου
 η
η  . Η κάθετη στην
. Η κάθετη στην  στο
στο  τέμνει την
τέμνει την  στο σημείο
στο σημείο  . Αν
. Αν  να υπολογιστεί το τμήμα,
να υπολογιστεί το τμήμα,  .Κατασκευάζεται γεωμετρικά το πιο πάνω τρίγωνο
.Κατασκευάζεται γεωμετρικά το πιο πάνω τρίγωνο ; )
; )Ενδεχομένως η ταξινόμηση να μην είναι η καλύτερη δυνατή αλλά μόλις συγκεντρώσω τις προταθείσες, θα την βελτιώσω.
για τους λάτρεις της Γεωμετρίας
