Χρησιμοποιούνται οι φάκελοι Γεωμετρίας Juniors, Γεωμετρίας Seniors, Γεωμετρίας A΄Λυκείου,Γεωμετρίας Β΄Λυκείου, Μόνο για Μαθητές, ΑΣΕΠ: Προτεινόμενα Θέματα, Γενικά Θέματα, Φάκελος Καθηγητή: Γενικά, Φάκελος Καθηγητή: Γεωμετρία εως τις ημερομηνίες εδώ
Όσα θεωρήματα βρίσκονται σε φυλλάδια υπάρχουν συγκεντρωμένα στα Φυλλάδια σε Διαγωνιστικά Μαθηματικά
Θεωρήματα με λέξεις
Θεώρημα των ίσων λόγων στο τετράπλευρο (δίνεται κυρτό (ή μη κυρτό, ή και στρεβλό) τετράπλευρο
 και έστω
και έστω  σημεία επί των πλευρών του
σημεία επί των πλευρών του  αντιστοίχως, τέτοια ώστε
αντιστοίχως, τέτοια ώστε  . Επί των
. Επί των  λαμβάνουμε αντιστοίχως τα εσωτερικά σημεία
λαμβάνουμε αντιστοίχως τα εσωτερικά σημεία  έτσι ώστε
έτσι ώστε  . Αποδείξτε ότι τα σημεία αυτά είναι συνευθειακά και ότι
. Αποδείξτε ότι τα σημεία αυτά είναι συνευθειακά και ότι  )
)Θεώρημα της Σπασμένης Χορδής του Αρχιμήδη (κι εδώ, εδώ) (πάνω σε ένα κύκλο, παίρνουμε τα σημεία
 και
και  και θεωρούμε
και θεωρούμε  το μέσο του κυρτογώνιου τόξου
το μέσο του κυρτογώνιου τόξου  . Θεωρούμε και το τυχαίο σημείο
. Θεωρούμε και το τυχαίο σημείο  του επίσης κυρτογώνιου τόξου
του επίσης κυρτογώνιου τόξου  .Αν
.Αν  είναι η προβολή του σημείου
είναι η προβολή του σημείου  πάνω στην χορδή
πάνω στην χορδή  τότε
τότε  )
)Θεώρημα Νότιου Πόλου (εδώ) (σε κάθε τρίγωνο
 η διχοτόμος μιας γωνίας(πχ της
η διχοτόμος μιας γωνίας(πχ της  ) και η μεσοκάθετος της τρίτης πλευράς (πχ της
) και η μεσοκάθετος της τρίτης πλευράς (πχ της  )τέμνονται σε σημείο του περιγεγραμμένου κύκλου του τριγώνου.)
)τέμνονται σε σημείο του περιγεγραμμένου κύκλου του τριγώνου.)Θεώρημα Πεταλούδας (κι εδώ, εδώ) (σε κύκλο με κέντρο Ο, έστω ΑΒ χορδή και Ι το μέσο της χορδής. ΓΔ,ΖΕ τυχαίες χορδές του κύκλου που διέρχονται από το Ι . Μ,Ν τα σημεία τομής των ΓΖ,ΕΔ με την ΑΒ αντίστοιχα τότε ΙΜ=ΙΝ)
Ιαπωνικό Θεώρημα (κι εδώ)(Σε κάθε εγγράψιμο τετράπλευρο,το άθροισμα των ακτίνων των εγγεγραμμένων κύκλων των τριγώνων,στα οποία χωρίζει το τετράπλευρο μια διαγώνιος του,ισούται με το αντίστοιχο άθροισμα των ακτίνων των εγγεγραμμένων κύκλων των τριγώνων που χωρίζει η άλλη διαγώνιος του τετραπλεύρου)
Γενικευμένο Θεώρημα Διχοτόμων
Θεώρημα Εσωτερικής και Εξωτερικής Διχοτόμου με εμβαδά, με Ν.Ημιτόνων
Πυθαγόρειο θεώρημα (κι εδώ, εδώ)
Εφαπτομένη αθροίσματος και διαφοράς γεωμετρικά
Ημίτονο αθροίσματος και διαφοράς από Θ. Πτολεμαίου
Ημίτονο - Συνημίτονο διπλάσιας γωνίας γεωμετρικά
Ημίτονο - Συνημίτονο τριπλάσιας γωνίας γεωμετρικά
Μετρικές Σχέσεις σε ορθογώνιο τρίγωνο κι αντίστροφα με διανύσματα
Θεωρήματα Διαμέσων με διανύσματα
Διάμεσος βάσης ισοσκελούς τριγώνου με διανύσματα
Διάμεσος υποτείνουσας κι αντίστροφο με διανύσματα
Τριγωνική Ανισότητα από Νόμο Συνημιτόνων
Ιδιότητα Μεσοκαθέτου διαφορετική
Θεωρήματα με ονόματα (αλφαβητικά)
Θεώρημα του Blackwell (σε κάθε ορθογώνιο τρίγωνο, τα ημικύκλια που έχουν διάμετρο τις πλευρές του τριγώνου και δεν έχουν άλλα κοινά σημεία με αυτό, εφάπτονται σε ένα τετράγωνο που έχει πλευρά την ημιπερίμετρο του τριγώνου)
Θεώρημα Brahmagupta (κι εδώ) (δύο κάθετες μεταξύ τους χορδές
 ενός κύκλου, τέμνονται στο
ενός κύκλου, τέμνονται στο  .νδο η κάθετη από το
.νδο η κάθετη από το  προς την
προς την  , διέρχεται από το μέσο
, διέρχεται από το μέσο  της
της  )
)Τύπος του Brahmagupta (κι εδώ) (Αν
 είναι τετράπλευρο εγγράψιμο σε κύκλο με
είναι τετράπλευρο εγγράψιμο σε κύκλο με  τότε
τότε  με
με  την ημιπερίμετρο του
την ημιπερίμετρο του  )
)Τύπος του Bretschneider (ας είναι
 οι πλευρές ενός τετραπλεύρου,
οι πλευρές ενός τετραπλεύρου,  οι διαγωνιές του και
οι διαγωνιές του και  οι δύο απέναντι γωνίες του.
οι δύο απέναντι γωνίες του.Να αποδείξετε ότι:
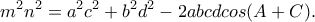 )
)Θεώρημα του Brianchon
Θεώρημα Carnot (κι εδώ)(σημείο Ρ προβάλλεται επι των πλευρών ΒΓ,ΓΑ,ΑΒ τριγώνου ΑΒΓ με αντίστοιχα ίχνη Δ, Ε, Ζ , τότε
 και αντιστρόφως)
και αντιστρόφως)Θεώρημα Casey
Ισότητα Casey (κι εδώ) (Θεωρούμε δύο κύκλους
 και το ριζικό άξονα αυτών
και το ριζικό άξονα αυτών  Αν
Αν  σημείο του επιπέδου και
σημείο του επιπέδου και  είναι η απόσταση του
είναι η απόσταση του  από την
από την  να αποδείξετε ότι:
να αποδείξετε ότι:  )
)Ceva τριγωνομετρικό
Θεώρημα του Feuerbach (κι εδώ) (σε κάθε τρίγωνο ο κύκλος των εννέα σημείων (Euler) εφάπτεται του εγγεγραμμένου και των τριών παρεγγεγραμμένων κύκλων του)
Θεώρημα του Desargues (κι εδώ, εδώ)(δέσμη τριών ευθειών συντρέχουν στο σημείο
 . Αντίστοιχα στην κάθε μία βρίσκονται τα ζεύγη σημείων
. Αντίστοιχα στην κάθε μία βρίσκονται τα ζεύγη σημείων  . Τα σημεία
. Τα σημεία  είναι τα σημεία τομής των τμημάτων
είναι τα σημεία τομής των τμημάτων  . Τότε τα
. Τότε τα  είναι συνευθειακά)
είναι συνευθειακά)Ευθεία Euler (κι εδώ, εδώ) (το ορθόκεντρο, βαρύκεντρο και περίκεντρο οξυγωνίου τριγώνου είναι συνευθειακά, κτλ)
Θεώρημα Euler (Αν Ο και Ι είναι τα κέντρα του περιγεγραμμένου και του εγγεγραμμένου κύκλου αντίστοιχα ενός τριγώνου ΑΒΓ και R , r οι ακτίνες τους (αντίστοιχα) τότε
 )
)Κύκλος Euler
Εyball theorem (κι εδώ) (Έστω δύο κύκλοι
 and
and  , με κέντρα
, με κέντρα  ,
,  και ακτίνες
και ακτίνες  ,
,  , αντίστοιχα. Έστω ότι οι εφαπτομένες από το
, αντίστοιχα. Έστω ότι οι εφαπτομένες από το  στο
στο  , τέμνουν τον
, τέμνουν τον  στα σημεία
στα σημεία  και
και  , ενώ οι εφαπτομένες από το
, ενώ οι εφαπτομένες από το  στο
στο  , τέμνουν τον
, τέμνουν τον  στα σημεία
στα σημεία  και
και  . Να αποδειχθεί ότι
. Να αποδειχθεί ότι  )
)πρόβλημα Fagnano - ορθικό τρίγωνο (την ελάχιστη περίμετρο τριγώνου σε οξυγώνιο τρίγωνο την έχει το ορθικό τρίγωνο)
Σημείο Gergonne (σε κάθε τρίγωνο ΑΒΓ οι ευθείες που συνδέουν τις κορυφές του με τα σημεία επαφής των πλευρών με τον εγγεγραμμένο κύκλο διέρχονται από το ίδιο σημείο,το ίδιο ισχύει για τις ευθείες εκείνες του τριγώνου αυτού που συνδέουν τις κορυφές με τα σημεία επαφής των πλευρών με τους παρεγγεγραμμένους κύκλους)
Θεώρημα του Καραθεοδωρή (κι εδώ) ( Στο εσωτερικό τριγώνου
 θεωρούμε τυχαίο σημείο
θεωρούμε τυχαίο σημείο  . Να δείξετε ότι :
. Να δείξετε ότι :  όπου
όπου  τα εμβαδά των τριγώνων
τα εμβαδά των τριγώνων  αντίστοιχα.)
αντίστοιχα.)Θεώρημα Leibnitz (κι εδώ) (για σημείο τυχαίο σημείο Ρ και βαρύκεντρο Κ τριγώνου ΑΒΓ ισχύει
 )
)Σημείο του Lemoine (κι εδώ, εδώ , εδώ, εδώ, εδώ) (σε κάθε τρίγωνο οι ευθείες που συνδέουν τα μέσα των υψών με τα μέσα των αντίστοιχων πλευρών συντρέχουν - στο σημείο Lemoine του τριγώνου, οι 3 συμμετροδιάμεσοι ενός τριγώνου διέρχονται από το ίδιο σημείο. Οι αποστάσεις αυτού του σημείου από τις πλευρές του τριγώνου είναι ανάλογες προς τις πλευρές. Είναι το σημείο του οποίου το άθροισμα των τετραγώνων των αποστάσεων από τις πλευρές του τριγώνου είναι ελάχιστο)
Θεώρημα MacLaurin (κι εδώ)(πάνω στις πλευρές γωνίας
 θεωρώ τα σημεία
θεωρώ τα σημεία  τέτοια ώστε
τέτοια ώστε  . Καθώς τα Α,Β μεταβάλλονται, οι περιγεγραμμένοι κύκλοι των σχηματιζομένων τριγώνων
. Καθώς τα Α,Β μεταβάλλονται, οι περιγεγραμμένοι κύκλοι των σχηματιζομένων τριγώνων  διέρχονται από σταθερό σημείο εκτός του Ο)
διέρχονται από σταθερό σημείο εκτός του Ο)Γενικότερο Θεώρημα MacLaurin (δύο σημεία
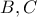 κινούνται επί των πλευρών γωνίας
κινούνται επί των πλευρών γωνίας 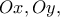 αντίστοιχα, ώστε να ισχύει
αντίστοιχα, ώστε να ισχύει  όταν
όταν  μήκη δοθέντων ευθυγράμμων τμημάτων και
μήκη δοθέντων ευθυγράμμων τμημάτων και  δοθέν ευθύγραμμο τμήμα. Η περιφέρεια
δοθέν ευθύγραμμο τμήμα. Η περιφέρεια  διέρχεται από δύο σταθερά σημεία)
διέρχεται από δύο σταθερά σημεία)Θεώρημα Μενελάου (διατύπωση εδώ)
Θεώρημα του Miquel (κι εδώ, εδώ) (Σε τετράπλευρο
 , που δεν είναι τραπέζιο, οι απέναντι πλευρές προεκτεινόμενες τέμνονται στα σημεία
, που δεν είναι τραπέζιο, οι απέναντι πλευρές προεκτεινόμενες τέμνονται στα σημεία  . Να αποδειχθεί ότι:
. Να αποδειχθεί ότι:1) Οι περιγεγραμμένοι κύκλοι των τριγώνων
 διέρχονται από κοινό σημείο
διέρχονται από κοινό σημείο  .
.2) Τα κέντρα
 των παραπάνω κύκλων είναι ομοκυκλικά σημεία και ότι το σημείο
των παραπάνω κύκλων είναι ομοκυκλικά σημεία και ότι το σημείο  βρίσκεται κι’ αυτό στον ίδιο κύκλο.
βρίσκεται κι’ αυτό στον ίδιο κύκλο.3) Οι προβολές
 του σημείου
του σημείου  στις πλευρές του αρχικού τετραπλεύρου είναι συνευθειακά σημεία..
στις πλευρές του αρχικού τετραπλεύρου είναι συνευθειακά σημεία..4) Αν το αρχικό τετράπλευρο είναι εγγράψιμο τότε το σημείο
 βρίσκεται στην ευθεία
βρίσκεται στην ευθεία  )
)Θεώρημα Monge d’ Alembert (κι εδώ) (δίνονται τρείς κύκλοι
 με
με  οι οποίοι είναι ανά δύο ο ένας εξωτερικά του άλλου
οι οποίοι είναι ανά δύο ο ένας εξωτερικά του άλλουi) Αν
 είναι τα σημεία τομής των κοινών εξωτερικών εφαπτομένων των ζευγαριών
είναι τα σημεία τομής των κοινών εξωτερικών εφαπτομένων των ζευγαριών  αντίστοιχα να δειχθεί ότι
αντίστοιχα να δειχθεί ότι  είναι συνευθειακά
είναι συνευθειακά ii) Αν
 είναι τα σημείο τομής των κοινών εσωτερικών εφαπτομένων των ζευγαριών
είναι τα σημείο τομής των κοινών εσωτερικών εφαπτομένων των ζευγαριών  αντίστοιχα να δειχθεί ότι:
αντίστοιχα να δειχθεί ότι:  είναι επίσης συνευθειακά)
είναι επίσης συνευθειακά)Θεώρημα του Morley (κι εδώ) (oι τριχοτόμοι τυχαίου τριγώνου, τεμνόμενες ανα δύο, σχηματίζουν πάντα ισόπλευρο τρίγωνο)
σημείο Nagel (το έγκεντρο
 το βαρύκεντρο
το βαρύκεντρο  και το σημείο Nagel
και το σημείο Nagel  , ανήκουν στην ίδια ευθεία και
, ανήκουν στην ίδια ευθεία και  )
)Θεώρημα του Ναπολέοντα (τα κέντρα των ισοπλεύρων τριγώνων που αναγράφονται επί των πλευρών τυχαίου τριγώνου, και όλα προς το εξωτερικό του ή όλα προς το εσωτερικό του μέρος, ορίζουν ισόπλευρο τρίγωνο)
Θεώρημα Newton (κι εδώ, εδώ) (Σε κάθε περιγράψιμο τετράπλευρο, οι ευθείες που συνδέουν τα σημεία επαφής του εγγεγραμμένου κύκλου στις απέναντι πλευρές, διέρχονται δια του σημείου τομής των διαγωνίων του. Σε κάθε περιγράψιμο τετράπλευρο, του κέντρο του εγγεγραμμένου κύκλου, ανήκει στην ευθεία που συνδέει τα μέσα των διαγωνίων του)
Ευθεία Newton - Gauss (κι εδώ) (θεωρούμε το πλήρες τετράπλευρο ΑΒΓΔΕΖ. Να αποδειχθεί ότι τα μέσα των διαγωνίων του ανήκουν στην αυτή ευθεία )
Θεώρημα Πάππου (Clairaut) (κι εδώ, εδώ) (Σε τρίγωνο
 κατασκευάζουμε προς το εξωτερικό μέρος του τριγώνου τα τυχαία παραλληλόγραμμα
κατασκευάζουμε προς το εξωτερικό μέρος του τριγώνου τα τυχαία παραλληλόγραμμα  και
και  .Έστω
.Έστω  και
και  . Κατασκευάζουμε το παραλληλόγραμμο
. Κατασκευάζουμε το παραλληλόγραμμο  . Να δειχθεί ότι:
. Να δειχθεί ότι:  )
)Θεώρημα του Πάππου (επί δύο ευθειών, τεμνόμενων ή μη, υπάρχουν οι τριάδες σημείων
 στην πρώτη και
στην πρώτη και  στην δεύτερη. Τα σημεία
στην δεύτερη. Τα σημεία  είναι τα σημεία τομής των τμημάτων
είναι τα σημεία τομής των τμημάτων  . Τότε τα
. Τότε τα  είναι συνευθειακά)
είναι συνευθειακά)Θεώρημα Pascal (Θεωρούμε εξάγωνο ΑΒΓΔΕΖ εγγεγραμένο σε περιφέρεια. Να αποδειχθεί ότι τα τρία ζεύγη (ΑΒ , ΕΔ), (ΒΓ , ΕΖ), (ΓΔ , ΖΑ) των απέναντι πλευρών ορίζουν τρία σημεία Κ , Λ , Μ τα οποία ανήκουν στην αυτή ευθεία.)
Θεώρημα του Pollock (Ορθογώνιο τρίγωνο ΑΒΓ είναι εγγεγραμμένο σε περιφέρεια. Προεκτείνουμε τις πλευρές ΑΒ, ΑΓ , που περιέχουν την ορθή γωνία και φέρουμε εφαπτόμενές για τα τόξα ΑΒ, ΑΓ, ΒΓ ώστε το σημείο επαφής να είναι το μέσο εκάστοτε του αποκοπτόμμενου τμήματος επι της εφαπτομένης υπό των ευθειών ΑΒ, ΑΓ. Να δειχθεί οτι τα 3 σημεία επαφής είναι κορυφές ισόπλευρου τριγώνου.)
Θεώρημα Pompeiu (θεωρούμε ισόπλευρο τρίγωνο ΑΒΓ και Ρ σημείο στο εσωτερικό του, τότε τα τμήματα ΡΑ, ΡΒ, ΡΓ αποτελούν μήκη πλευρών τριγώνου)
Θεώρημα Πτολεμαίου (σε κάθε εγγράψιμο τετράπλευρο το γινόμενο των διαγωνίων ισούται με το άθροισμα των γινομένων των απέναντι πλευρών)
Ανισότητα του Πτολεμαίου(σε κάθε μη εγγράψιμο τετράπλευρο το γινόμενο των διαγωνίων ισούται με το άθροισμα των γινομένων των απέναντι πλευρών)
Ευθεία Simson
Ευθεία Steiner (τα συμμετρικά σημείου του περιγεγραμμένου κύκλου τριγώνου ΑΒΓ ως προς τι ευθείες ΑΒ,ΑΓ και ΒΓ είναι σημεία συνευθείακα)
Θεώρημα Steiner - Lehmus (κι εδώ, εδώ, εδώ, εδώ, εδώ, εδώ) (αν ένα τρίγωνο έχει δύο διχοτόμους ίσες, τότε είναι ισοσκελές)
Θεώρημα των Steiner - Fermat - Toricelli (κι εδώ , εδώ, εδώ, εδώ, εδώ) (αν σε ένα τρίγωνο ΑΒΓ στο οποίο κάθε γωνία είναι μικρότερη των 120, κατασκευάσουμε εξωτερικά αυτού τα ισόπλευρα τρίγωνα ΑΒΓ',ΑΓΒ',ΒΓΑ', τότε τα τμήματα ΑΑ',ΒΒ',ΓΓ' είναι ίσα και διέρχονται από το ίδιο σημείο, που έχει το ελάχιστο άθροισμα αποστάσεων από τις κορυφές του τριγώνου)
Γενίκευση του Θεωρήματος του Steiner (δίνεται τυχαίο τρίγωνο
 και τα όμοια ισοσκελή τρίγωνα
και τα όμοια ισοσκελή τρίγωνα  (
( ) προς το «εξωτερικό μέρος του τριγώνου
) προς το «εξωτερικό μέρος του τριγώνου  ) . Να δειχθούν οι εξής προτάσεις:
) . Να δειχθούν οι εξής προτάσεις:i) Αν
 τότε διέρχονται από το ίδιο σημείο
τότε διέρχονται από το ίδιο σημείο 
ii) Τα τρίγωνα
 και
και  έχουν το ίδιο βαρύκεντρο
έχουν το ίδιο βαρύκεντρο 
iii) Οι ευθείες
 διέρχονται από το ίδιο σημείο
διέρχονται από το ίδιο σημείο 
iv) Αν
 είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου  κ τότε τα σημεία
κ τότε τα σημεία  είναι συνευθειακά.)
είναι συνευθειακά.)Θεώρημα Stewart (δίνεται τρίγωνο ΑΒΓ και Ρ τυχαίο σημείο της ευθείας ΒΓ, να δείξετε ότι ισχύει:
 )
)Θεώρημα Sylvestr (τα σημεία Α, Β, Γ σχηματίζουν τρίγωνο.Αν οι διανυσματικές τους ακτίνες έχουν ίσα μέτρα, το άθροισμά τους ισούται με την διανυσματική ακτίνα του ορθόκεντρου του ΑΒΓ)
κύκλος Taylor (Δίνεται τρίγωνο
 και έστω
και έστω  τα ύψη του. Αν
τα ύψη του. Αν  είναι οι ορθές προβολές του
είναι οι ορθές προβολές του  στις πλευρές
στις πλευρές  αντίστοιχα,
αντίστοιχα,  είναι οι ορθές προβολές του
είναι οι ορθές προβολές του  στις πλευρές
στις πλευρές  αντίστοιχα και τέλος
αντίστοιχα και τέλος  είναι οι ορθές προβολές του
είναι οι ορθές προβολές του  στις πλευρές
στις πλευρές  αντίστοιχα να δειχθεί ότι τα σημεία
αντίστοιχα να δειχθεί ότι τα σημεία  είναι ομοκυκλικά)
είναι ομοκυκλικά)Θεώρημα Thebault (ένα τρίγωνο
 είναι εγγεγραμμένο σε κύκλο
είναι εγγεγραμμένο σε κύκλο  . Στην πλευρά
. Στην πλευρά  παίρνουμε σημείο
παίρνουμε σημείο  . Ένας κύκλος με κέντρο
. Ένας κύκλος με κέντρο  εφάπτεται με τα τμήματα
εφάπτεται με τα τμήματα  και με τον κύκλο
και με τον κύκλο  στο
στο 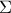 (το
(το 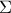 είναι σημείο του
είναι σημείο του  ). Ένας άλλος κύκλος με κέντρο
). Ένας άλλος κύκλος με κέντρο  εφάπτεται με τα τμήματα
εφάπτεται με τα τμήματα  και με τον κύκλο
και με τον κύκλο  στο
στο  . Αν
. Αν  είναι το έγκεντρο του τριγώνου
είναι το έγκεντρο του τριγώνου  , να αποδειχθεί ότι τα σημεία
, να αποδειχθεί ότι τα σημεία  είναι συνευθειακά.)
είναι συνευθειακά.)Θεώρημα Van Aubel (κι εδώ)(έστω
 εσωτερικό σημείο τρίγωνου
εσωτερικό σημείο τρίγωνου  . Οι
. Οι  τέμνουν τις πλευρές του τριγώνου, στα σημεία
τέμνουν τις πλευρές του τριγώνου, στα σημεία  αντίστοιχα. Τότε
αντίστοιχα. Τότε  )
)Θεώρημα Van Schooten (κι εδώ, εδώ, εδώ) (έστω το ισόπλευρο τρίγωνο ΑΒΓ και ο περιγεγραμμένος του κύκλος. Αν Μ σημείο του ελάσσονος τόξου ΑΒ (διαφορετικό απο τα Α,Β), τότε ΜΓ=ΜΑ+ΜΒ)
Θεώρημα Vecten (κι εδώ , εδώ, εδώ, εδώ , εδώ, εδώ, εδώ, εδώ) (επί των πλευρών ΑΒ και ΑΓ ενός τριγώνου ΑΒΓ και εκτός αυτού, κατασκευάζουμε τα τετράγωνα ΑΒΔΕ και ΑΓΖΚ. Οι ευθείες ΒΖ και ΓΔ τέμνονται επί του ύψους ΑΘ του τριγώνου ΑΒΓ)
Θεωρήματος Viviani επέκταση (έστω ισόπλευρο τρίγωνο
 και σημείο
και σημείο  του περιγεγραμμένου του κύκλου
του περιγεγραμμένου του κύκλου  . Στο
. Στο  εφάπτεται εξωτερικά του
εφάπτεται εξωτερικά του  άλλος κύκλος
άλλος κύκλος  . Αν
. Αν  τα μήκη των εφαπτόμενων τμημάτων στον
τα μήκη των εφαπτόμενων τμημάτων στον  , να δειχθεί ότι ένα απ’ αυτά ισούται με το άθροισμα των 2 άλλων, δηλαδή
, να δειχθεί ότι ένα απ’ αυτά ισούται με το άθροισμα των 2 άλλων, δηλαδή  )
)Αντίστροφα Προτάσεων
αντίστροφο ιδιότητας βαρυκέντρου
αντίστροφο ιδιότητας γωνίας
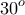 σε ορθογώνιο τρίγωνο (κι εδώ)
σε ορθογώνιο τρίγωνο (κι εδώ)αντίστροφο διαμέσου τραπεζίου
αντίστροφο θεωρήματος Euler
αντίστροφο μετρικής σχέσης ύψους που αντιστοιχεί σε υποτείνουσα (κι εδώ, εδώ)
απέναντι από άνισες γωνίες βρίσκονται όμοια άνισες πλευρές
Προτάσεις
λήμμα για ευθεία διερχόμενη από βαρύκεντρο (κι εδώ) (αν μια ευθεία που περνάει από το βαρύκεντρο ενός τριγώνου
 τέμνει τις πλευρές
τέμνει τις πλευρές  στα σημεία
στα σημεία  , τότε ισχύει ότι :
, τότε ισχύει ότι :  )
)πρόταση στα αμφιγράψιμα τετράπλευρα (κι εδώ) (ένα αμφιγράψιμο τετράπλευρο έχει εγγεγραμμένο και περιγεγραμμένο κύκλο. Αποδείξτε ότι τα κέντρα αυτών των κύκλων και το σημείο τομής των διαγωνίων του, ανήκουν στην ίδια ευθεία)
κοινή χορδή τεμνόμενων κύκλων (η κοινή χορδή 2 τεμνόμενων κύκλων διέρχεται από το μέσο της κοινής εφαπτόμενης τους)
για πλήρες τετράπλευρο
(i) Τα κέντρα των περιγεγραμμένων κύκλων των τεσσάρων τριγώνων πλήρους τετραπλεύρου είναι ομοκυκλικά και το περικύκλιό τους διέρχεται από το σημείο Miquel του πλήρους τετραπλεύρου
ii) Τα μέσα των τμημάτων
 ανήκουν στην ευθεία του Simson του σημείου
ανήκουν στην ευθεία του Simson του σημείου  ως προς το τρίγωνο
ως προς το τρίγωνο 
iii) Τα ίχνη των καθέτων από το σημείο
 του Miquel του πλήρους τετραπλεύρου στις πλευρές του είναι σημεία συνευθειακά
του Miquel του πλήρους τετραπλεύρου στις πλευρές του είναι σημεία συνευθειακάiv) Τα ορθόκεντρα των τεσσάρων τριγώνων του πλήρους τετραπλεύρου είναι σημεία συνευθειακά
v) Οι κύκλοι με διαμέτρους τις διαγώνιες του πλήρους τετραπλεύρου έχουν κοινό ριζικό άξονα )
vi) οι διαγώνιες πλήρους τετραπλεύρου τέμνονται αρμονικά
vi) τα μέσα διαγωνίων πλήρους τετραπλεύρου είναι συνευθειακά (Ευθεία Newton Gauss) (κι εδώ)
vii)οι διχοτόμοι των προεκτάσεων των πλευρών ενός κυκλικού τετραπλεύρου τέμνονται κάθετα, πάνω στην ευθεία που συνδέει τα μέσα των διαγωνίων του
viii) η ευθεία Simson σημείου Μ διχοτομεί το ευθύγραμμο τμήμα ΜΗ όπου Η είναι το ορθόκεντρο του τριγώνου
ix) τα ορθόκεντρα των τεσσάρων τριγώνων πλήρους τετραπλεύρου βρίσκονται πάνω σε μια ευθεία η οποία είναι ομοιόθετη της ευθείας Miquel του τετραπλεύρου αυτού κατά την ομοιοθεσία
 όπου
όπου  είναι το σημείο Miquel του πλήρους τετραπλεύρο
είναι το σημείο Miquel του πλήρους τετραπλεύροκριτήριο καθετότητας (
 )
)κριτήριο ρόμβου ως περιγράψιμου τετραπλεύρου (το έγκεντρο και το βαρύκεντρο περιγράψιμου τετραπλεύρου ταυτίζονται αν και μόνον αν αυτό είναι ρόμβος)
Προβλήματα
Πρόβλημα του Πειρατή από Σωτήρη Λουρίδα (κι εδώ) (Ένας Αρχηγός πειρατής πήγε σε ενα ξερονήσι και έθαψε τον θησαυρό σε ένα σημείο με βάση τρία δένδρα μία μπανανιά (Α), μία χουρμαδιά (Γ) και ένα ξερόδενδρο(Β), κοντά στην ακτή ως εξής: Έσκαψε προς τα έξω από την περιοχή που όριζαν τα δέντρα και κάθετα στην ΒΑ (από το Α) και σημάδεψε σημείο Κ ώστε ΚΑ=ΑΒ, μετά προς τα έξω από την περιοχή που όριζαν τα δέντρα και κάθετα στην ΒΓ (από το Γ) και σημάδεψε σημείο Λ ωστε ΓΛ=ΓΒ. Στην συνέχεια σκάβοντας κατά ευθεία ένωσε τα σημεία Κ,Λ και βρήκε το μέσο του ΚΛ όπου έθαψε τον θησαυρό, αφαιρώντας στην συνέχεια επιμελώς κάθε ίχνος. Μετά από ενα χρόνο επέστρεψε και διαπίστωσαν ότι το ξερόδενδρο δεν υπήρχε. Όλοι πάγωσαν αλλά ο Αρχηγός πειρατής ξεκαρδίστηκε στα γέλια.Γιατί άραγε τόση ευτυχία;)
Ναυαγοσωστικό από Νίκο Φραγκάκη
Περί Λημμάτων από Αρχιμήδη (αρίθμηση από εδώ)
Πρόταση 1
Πρόταση 2 (Έστω κύκλος
 και σημείο
και σημείο  του επιπέδου του εκτός αυτού.Ας είναι
του επιπέδου του εκτός αυτού.Ας είναι 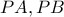 τα εφαπτόμενα τμήματα στον κύκλο (
τα εφαπτόμενα τμήματα στον κύκλο (  ) και
) και  το αντιδιαμετρικό (ως προς τον
το αντιδιαμετρικό (ως προς τον  ) του
) του  . Αν
. Αν  και
και  , να δειχθεί ότι
, να δειχθεί ότι  .)
.)Πρόταση 3
Πρόταση 4
Πρόταση 5 (Σε τυχαίο σημείο
 της διαμέτρου
της διαμέτρου  ημικυκλίου
ημικυκλίου  φέρνουμε την κάθετη
φέρνουμε την κάθετη  . Με διαμέτρους τις
. Με διαμέτρους τις  και
και  γράφουμε ημικύκλια
γράφουμε ημικύκλια  αντίστοιχα στο εσωτερικό του ημικυκλίου
αντίστοιχα στο εσωτερικό του ημικυκλίου  . Αν
. Αν  είναι ο κύκλος που εφάπτεται του
είναι ο κύκλος που εφάπτεται του  , του
, του  και της ημιευθείας
και της ημιευθείας  και
και  ο κύκλος που εφάπτεται του
ο κύκλος που εφάπτεται του  , του
, του  και της ημιευθείας
και της ημιευθείας  να δειχθεί ότι οι κύκλοι
να δειχθεί ότι οι κύκλοι  και
και  είναι ίσοι.)
είναι ίσοι.)Πρόταση 6
Πρόταση 7
Πρόταση 8 (τριχοτόμηση γωνίας με τη μέθοδο της νεύσης)
Πρόταση 9
Πρόταση 10
Πρόταση 11
Πρόταση 12 (κι εδώ ?) (Οι πλευρές
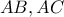 τριγώνου
τριγώνου  εφάπτονται στα σημεία
εφάπτονται στα σημεία  ημικυκλίου με διάμετρο
ημικυκλίου με διάμετρο  επί της
επί της  . Αν
. Αν  τέμνονται στο
τέμνονται στο  , δείξτε ότι :
, δείξτε ότι :  )
)Πρόταση 13
Πρόταση 14
Πρόταση 15
Απολλώνιο πρόβλημα
το Απολλώνιο πρόβλημα στον χώρο
λύσεις στο Απολλώνιο πρόβλημα
Υ.Γ. Τα Γεωμετρικά Ακρότατα, τα πολύγωνα εφαπτόμενα/εγγεγραμμένα σε πολύγωνα, οι αφιερώσεις του Στάθη καθώς και τα προτεινόμενα θέματα του KARKAR, οι 3d λύσεις μεταφέρθηκαν όλα στο Bulletin ΒΛΓΕΩ (φάκελο Β' Λυκείου Γεωμετρίας)
για τους λάτρεις της Γεωμετρίας
