Το προτείνω γιατί το θεωρώ ως απαραίτητη γνώση για παιδιά που ασχολούνται με μαθηματικούς διαγωνισμούς.
'Εστω
 τα μήκη πλευρών ενός τριγώνου
τα μήκη πλευρών ενός τριγώνου 
Αποδείξτε ότι τα

είναι μήκη πλευρών ενός οξυγωνίου τριγώνου
 με μικρότερη περίμετρο από αυτήν του
με μικρότερη περίμετρο από αυτήν του  , εκτός αν το
, εκτός αν το  είναι ισόπλευρο.
είναι ισόπλευρο.Τι μπορεί να λεχθεί για το εμβαδόν του
 συγκριτικά με το εμβαδόν του
συγκριτικά με το εμβαδόν του  ;
;
 τέτοιοι ώστε
τέτοιοι ώστε 

 τότε παίρνουμε
τότε παίρνουμε  κι έτσι
κι έτσι  .
. πλευρές τριγώνου και για να είναι οξυγώνιο αρκεί να αποδείξουμε ότι
πλευρές τριγώνου και για να είναι οξυγώνιο αρκεί να αποδείξουμε ότι  (που προκύπτει με μία ύψωση στο τετράγωνο) και
(που προκύπτει με μία ύψωση στο τετράγωνο) και  (που είναι άμεσο με αντικατάσταση) αντίστοιχα.
(που είναι άμεσο με αντικατάσταση) αντίστοιχα. και
και  η περίμετρος του τριγώνου
η περίμετρος του τριγώνου 
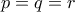 δηλαδή
δηλαδή  που σημαίνει ότι το
που σημαίνει ότι το 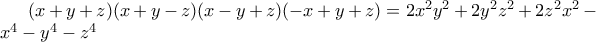 και πράξεις μεταξύ των:
και πράξεις μεταξύ των:

 γίνονται με την βοήθεια των δοσμένων ισοτήτων:
γίνονται με την βοήθεια των δοσμένων ισοτήτων: αντίστοιχα, οπου
αντίστοιχα, οπου  η ημιπερίμετρος του
η ημιπερίμετρος του  η οποία μετα απο πράξεις και αντικαταστάσεις γίνεται:
η οποία μετα απο πράξεις και αντικαταστάσεις γίνεται: που ισχύει (τριγωνική ανισότητα).
που ισχύει (τριγωνική ανισότητα).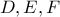 τα σημεία επαφής των πλευρών
τα σημεία επαφής των πλευρών  με τον εγγεγραμμένο κύκλο.
με τον εγγεγραμμένο κύκλο.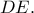 Θα χρησιμοποιηθεί ο νόμος του συνημιτόνου στο τρίγωνο
Θα χρησιμοποιηθεί ο νόμος του συνημιτόνου στο τρίγωνο 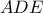 , η πρώτη σκέψη που έρχεται στο μυαλό...
, η πρώτη σκέψη που έρχεται στο μυαλό...








 και ότι
και ότι 
 σχηματίζουν τρίγωνο και αφού είναι γνωστό ότι το τρίγωνο που έχει κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου με τις πλευρές του
σχηματίζουν τρίγωνο και αφού είναι γνωστό ότι το τρίγωνο που έχει κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου με τις πλευρές του  .
. την ακτίνα του περιγεγραμμένου κύκλου που έχει μήκη πλευρών
την ακτίνα του περιγεγραμμένου κύκλου που έχει μήκη πλευρών  και έτσι
και έτσι 




 γι' αυτό είχαμε ισότητα εμβαδών. Η ουσία δεν αλλάζει όμως...
γι' αυτό είχαμε ισότητα εμβαδών. Η ουσία δεν αλλάζει όμως...