Για το β) που από ότι βλέπω έμεινε...
Καθώς το

κινείται πάνω στην

ορίζει ίσους διπλούς λόγους με το

στην

αφού συνδέονται μέσω προβολής ως προς τον πόλο

.Άρα η τομή των

,έστω

,η οποία βρίσκεται και στην

,κινείται πάνω σε κωνική.Στο συγκεκριμένο παράδειγμα η κωνική περνάει από τα

άρα είναι η υπερβολή του

.Από εδώ το ζητούμενο έπεται από ένα (γνωστό) λήμμα που οφείλεται στον

:
Αν  ο σεβιανός κύκλος σημείου
ο σεβιανός κύκλος σημείου  ως προς το
ως προς το  ,τότε αυτός ο κύκλος περνάει από το κέντρο της υπερβολής
,τότε αυτός ο κύκλος περνάει από το κέντρο της υπερβολής 
.Παραθέτω μια απόδειξη που έχω υπόψη μου που βασίζεται σε 3 επιπλέον (κάποια γνωστά) λήμματα:
1.
Ο ισογώνιος μετασχηματισμός ως προς τρίγωνο στέλνει περιγεγραμμένες κωνικές του τριγώνου σε ευθείες
Απόδειξη:Στα γρήγορα,εδώ(το αντίστροφο) :
viewtopic.php?f=178&t=62253&p=306081#p306081 .
2.
Αν  ο ποδικός κύκλος σημείου
ο ποδικός κύκλος σημείου  ως προς το
ως προς το  ,τότε αυτός ο κύκλος περνάει από το κέντρο της υπερβολής
,τότε αυτός ο κύκλος περνάει από το κέντρο της υπερβολής 
.
Απόδειξη(χωρίς σχήμα):Αν πάρουμε το ισογώνιο του

,έστω

είναι γνωστό ότι έχει τον ίδιο ποδικό κύκλο.Το

τώρα διαγράφει ευθεία από το 1.Επιπλέον,αυτή η ευθεία περνάει από το περίκεντρο του τριγώνου,αφού είναι ισογώνια υπερβολής που περνάει από το ορθόκεντρο του τριγώνου.Από το 2ο θεώρημα του

λοιπόν,οι ποδικοί κύκλοι των

(άρα και των

) τέμνονται πάνω στον κύκλο του

του

σε σημείο

.Στέλνοντας το

στο άπειρο (από τις δύο μεριές της υπερβολής),ο ποδικός κύκλος γίνεται ασύμπτωτος ευθεία,άρα τελικά το

είναι το κέντρο της υπερβολής.

- feuerbach family '..1.png (41.42 KiB) Προβλήθηκε 2999 φορές
3.
Έστω  τρίγωνα και
τρίγωνα και  .Αν τα
.Αν τα  και τα
και τα  είναι προοπτικά ζεύγη τριγώνων,τότε τα
είναι προοπτικά ζεύγη τριγώνων,τότε τα  βρίσκονται σε κωνική,με
βρίσκονται σε κωνική,με  τα αντίστοιχα κέντρα προοπτικότητας.(και αντίστροφα).
τα αντίστοιχα κέντρα προοπτικότητας.(και αντίστροφα).
Απόδειξη:Δείχνουμε το αντίστροφο,αφού λόγω μοναδικότητας (έχει μερικές λεπτομέρειες το επιχείρημα) αν ισχύει το αντίστροφο ισχύει και το ευθύ.Αλλάζουμε τη διαδικασία:Επιλέγουμε σημείο

στην κωνική,έπειτα ορίζουμε ως

την τομή

και κωνικής και ως

την τομή

και κωνικής.Καθώς κινείται το

επί της κωνικής,επειδή οι

περνούν από σταθερό σημείο

,οι σημειοσειρές

βρίσκονται σε ενέλιξη (ενέλιξη σε κωνική,πχ.θεώρημα 1.5 εδώ -ή μάλλον το αντίστροφό του
https://www.google.com/url?sa=t&source= ... BS1VOwzYU0 ) και άρα έχουν ίσους διπλούς λόγους.Άρα

είναι προβολική σύνδεση.Ομοίως και η

είναι προβολική σύνδεση.Άρα και η

είναι προβολική σύνδεση.Με απλό τσεκάρισμα θέσης(για

) οι

περνούν από το

δηλαδή τα 3 ζεύγη

είναι συζυγή σε ενέλιξη.Λόγω του ότι οι σημειοσειρές

διαγράφουν ίσους διπλούς λόγους,είναι τελικά συζυγή της ίδιας ενέλιξης (το

ορίζεται μονοσήμαντα ώστε να έχουμε ισότητα διπλών λόγων ως η τομή

και κωνικής).Άρα τελικά

επίσης συνευθειακά.Μένει να δειχθεί η προοπτικότητα των

.Αν οριστεί

η τομή

και κωνικής (καθώς κινείται το

),λόγω του σταθερού

τα

βρίσκονται σε ενέλιξη δηλαδή διαγράφουν ίσους διπλούς λόγους.Όμοια,αν οριστεί

η τομή

και κωνικής και

και κωνικής αντίστοιχα, και επειδή τα

διαγράφουν ίσους διπλούς λόγους από τα παραπάνω,τα

διαγράφουν και αυτά ίσους διπλούς λόγους.Θέλουμε να δείξουμε ότι ταυτίζονται αυτά τα 3 σημεία,οπότε αρκεί να δειχτεί ότι ταυτίζονται για 3 θέσεις,αφού μετά κατασκευάζονται μονοσήμαντα οι υπόλοιπες θέσεις ώστε κάθε τετράδα να έχει ίσο διπλό λόγο με τις άλλες.Με απλό έλεγχο θέσης (για

) κάτι τέτοιο συμβαίνει,πράγμα που αποδεικνύει και το τρίτο λήμμα.

- feuerbach family '...2.png (66.42 KiB) Προβλήθηκε 2999 φορές
Για να δειχθεί η αρχική πρόταση του

,παίρνουμε τα παράκεντρα του σεβιανού του

(

),έστω

.Από το τρίτο λήμμα,τα

βρίσκονται στην ίδια κωνική,όπου

το ορθόκεντρο του

.Από το δεύτερο λήμμα,το κέντρο της κωνικής βρίσκεται πάνω στο ποδικό του

ως προς το

,δηλαδή πάνω στον

και η αρχική πρόταση δείχτηκε.
Για το πρόβλημα τώρα,έχουμε πως οι σεβιανοί κύκλοι σημείων επί της υπερβολής του

τέμνουν τον κύκλο του

στο κέντρο της υπερβολής αυτής.Αν πάρουμε το σημείο

του τριγώνου,το οποίο βρίσκεται πάνω σε αυτή την υπερβολή,ο σεβιανός του κύκλος (ο εγγεγραμμένος) τέμνει (εφάπτεται) στον κύκλο του

στο σημείο του

πράγμα που αποδεικνύει και το αρχικό ζητούμενο.
(Σημ.Το λήμμα 2 αν και ίσως να μην είναι απαραίτητο σημείο για κάποια λύση,ουσιαστικά δείχνει πως ο ποδικός κύκλος σημείου πάνω στην υπερβολή του

έχει και αυτός την ίδια ιδιότητα με τον σεβιανό κλπ...)
 και
και  οι πόλοι του (*). Θα λέμε ότι το
οι πόλοι του (*). Θα λέμε ότι το  αντιστοιχεί στην κορυφή
αντιστοιχεί στην κορυφή  ή στo ζεύγος πλευρών
ή στo ζεύγος πλευρών  και
και  , το
, το  στη κορυφή
στη κορυφή  και
και  στην
στην  . Θεωρούμε τυχαίο σημείο
. Θεωρούμε τυχαίο σημείο  της ευθείας
της ευθείας  και το ενώνουμε με τους πόλους
και το ενώνουμε με τους πόλους  . Οι ευθείες
. Οι ευθείες  και
και  τέμνουν τις ευθείες
τέμνουν τις ευθείες  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα (βλέπε σχήμα). Τότε
αντίστοιχα (βλέπε σχήμα). Τότε διέρχεται από τον πόλο
διέρχεται από τον πόλο 
 είναι ίχνη σεβιανών του τριγώνου
είναι ίχνη σεβιανών του τριγώνου 
 διέρχεται από το σημείο Feuerbach του τριγώνου
διέρχεται από το σημείο Feuerbach του τριγώνου 


 είναι συνευθειακά.
είναι συνευθειακά. είναι προοπτικά ως προς άξονα.
είναι προοπτικά ως προς άξονα. να τέμνονται επι της
να τέμνονται επι της  . Τότε από Μενέλαο :
. Τότε από Μενέλαο : . To
. To  όμως είναι το αρμονικό συζυγές του
όμως είναι το αρμονικό συζυγές του  και το
και το  το αρμονικό συζυγές του
το αρμονικό συζυγές του  οπότε
οπότε που ισοδυναμεί με τα σημεία
που ισοδυναμεί με τα σημεία  να είναι συνευθειακά.
να είναι συνευθειακά.
 προκύπτει ότι
προκύπτει ότι  .
. είναι τα σημεία τομής των
είναι τα σημεία τομής των  με τις πλευρές του τριγώνου ).
με τις πλευρές του τριγώνου ).
 - τέμνουσα
- τέμνουσα  .
.
 .
.
 'Ομοια το εφαρμόζουμε και για τα σημεία
'Ομοια το εφαρμόζουμε και για τα σημεία οπότε προκύπτει
οπότε προκύπτει


 και τυχαίο σημείο
και τυχαίο σημείο .
. τα σημεία τομής των
τα σημεία τομής των με την
με την  και
και  με την
με την  .
. . Αποδεικνύεται τότε ότι ο περιγεγραμμένος του
. Αποδεικνύεται τότε ότι ο περιγεγραμμένος του  .
.
 τότε στα τρίγωνα που ορίσαμε περιλαμβάνεται και αυτό που ορίζεται από τα σημεία επαφής του εγγεγραμμένου με τις πλευρές οπότε το
τότε στα τρίγωνα που ορίσαμε περιλαμβάνεται και αυτό που ορίζεται από τα σημεία επαφής του εγγεγραμμένου με τις πλευρές οπότε το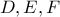 στις πλευρές
στις πλευρές αντίστοιχα. Έστω σημείο
αντίστοιχα. Έστω σημείο στην
στην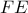 και σημεία
και σημεία και
και . Έστω
. Έστω τα σημεία τομής του περίκυκλου του
τα σημεία τομής του περίκυκλου του  με τις
με τις  συντρέχουν στον περίκυκλο του
συντρέχουν στον περίκυκλο του  το σημείο τομής της
το σημείο τομής της με τον περίκυκλο του
με τον περίκυκλο του με την
με την ,
,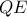 με την
με την και
και με την
με την συνευθειακά. Ομοίως
συνευθειακά. Ομοίως συνευθειακά και έτσι έχουμε το ζητούμενο.
συνευθειακά και έτσι έχουμε το ζητούμενο.
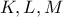 ίχνη σεβιανών στις πλευρές του τριγώνου .Τότε υπάρχει κωνική που διέρχεται από τα
ίχνη σεβιανών στις πλευρές του τριγώνου .Τότε υπάρχει κωνική που διέρχεται από τα οι περιγεγραμμένοι κύκλοι των τριγώνων
οι περιγεγραμμένοι κύκλοι των τριγώνων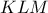 τέμνονται επί αυτής.
τέμνονται επί αυτής. τέμνονται στον κύκλο του Euler ,έστω στο
τέμνονται στον κύκλο του Euler ,έστω στο .
. είναι συνευθειακά οπότε τα
είναι συνευθειακά οπότε τα ανήκουν σε κωνική (από το αντίστροφο του Pascal).
ανήκουν σε κωνική (από το αντίστροφο του Pascal). ανήκουν σε κωνική .
ανήκουν σε κωνική .  ,έστω
,έστω  ,κινείται πάνω σε κωνική.Στο συγκεκριμένο παράδειγμα η κωνική περνάει από τα
,κινείται πάνω σε κωνική.Στο συγκεκριμένο παράδειγμα η κωνική περνάει από τα  άρα είναι η υπερβολή του
άρα είναι η υπερβολή του  .Από εδώ το ζητούμενο έπεται από ένα (γνωστό) λήμμα που οφείλεται στον
.Από εδώ το ζητούμενο έπεται από ένα (γνωστό) λήμμα που οφείλεται στον  :
: ο σεβιανός κύκλος σημείου
ο σεβιανός κύκλος σημείου  .Παραθέτω μια απόδειξη που έχω υπόψη μου που βασίζεται σε 3 επιπλέον (κάποια γνωστά) λήμματα:
.Παραθέτω μια απόδειξη που έχω υπόψη μου που βασίζεται σε 3 επιπλέον (κάποια γνωστά) λήμματα: ο ποδικός κύκλος σημείου
ο ποδικός κύκλος σημείου  ως προς το
ως προς το  .
. είναι γνωστό ότι έχει τον ίδιο ποδικό κύκλο.Το
είναι γνωστό ότι έχει τον ίδιο ποδικό κύκλο.Το  λοιπόν,οι ποδικοί κύκλοι των
λοιπόν,οι ποδικοί κύκλοι των  του
του  τρίγωνα και
τρίγωνα και  .Αν τα
.Αν τα  και τα
και τα  είναι προοπτικά ζεύγη τριγώνων,τότε τα
είναι προοπτικά ζεύγη τριγώνων,τότε τα  βρίσκονται σε κωνική,με
βρίσκονται σε κωνική,με  τα αντίστοιχα κέντρα προοπτικότητας.(και αντίστροφα).
τα αντίστοιχα κέντρα προοπτικότητας.(και αντίστροφα). στην κωνική,έπειτα ορίζουμε ως
στην κωνική,έπειτα ορίζουμε ως  την τομή
την τομή  και κωνικής και ως
και κωνικής και ως  την τομή
την τομή  και κωνικής.Καθώς κινείται το
και κωνικής.Καθώς κινείται το  περνούν από σταθερό σημείο
περνούν από σταθερό σημείο  ,οι σημειοσειρές
,οι σημειοσειρές  βρίσκονται σε ενέλιξη (ενέλιξη σε κωνική,πχ.θεώρημα 1.5 εδώ -ή μάλλον το αντίστροφό του
βρίσκονται σε ενέλιξη (ενέλιξη σε κωνική,πχ.θεώρημα 1.5 εδώ -ή μάλλον το αντίστροφό του  είναι προβολική σύνδεση.Ομοίως και η
είναι προβολική σύνδεση.Ομοίως και η  είναι προβολική σύνδεση.Άρα και η
είναι προβολική σύνδεση.Άρα και η  είναι προβολική σύνδεση.Με απλό τσεκάρισμα θέσης(για
είναι προβολική σύνδεση.Με απλό τσεκάρισμα θέσης(για  ) οι
) οι  περνούν από το
περνούν από το  δηλαδή τα 3 ζεύγη
δηλαδή τα 3 ζεύγη  είναι συζυγή σε ενέλιξη.Λόγω του ότι οι σημειοσειρές
είναι συζυγή σε ενέλιξη.Λόγω του ότι οι σημειοσειρές  διαγράφουν ίσους διπλούς λόγους,είναι τελικά συζυγή της ίδιας ενέλιξης (το
διαγράφουν ίσους διπλούς λόγους,είναι τελικά συζυγή της ίδιας ενέλιξης (το  και κωνικής).Άρα τελικά
και κωνικής).Άρα τελικά  επίσης συνευθειακά.Μένει να δειχθεί η προοπτικότητα των
επίσης συνευθειακά.Μένει να δειχθεί η προοπτικότητα των  η τομή
η τομή  και κωνικής (καθώς κινείται το
και κωνικής (καθώς κινείται το  βρίσκονται σε ενέλιξη δηλαδή διαγράφουν ίσους διπλούς λόγους.Όμοια,αν οριστεί
βρίσκονται σε ενέλιξη δηλαδή διαγράφουν ίσους διπλούς λόγους.Όμοια,αν οριστεί  η τομή
η τομή  και κωνικής και
και κωνικής και  και κωνικής αντίστοιχα, και επειδή τα
και κωνικής αντίστοιχα, και επειδή τα  διαγράφουν ίσους διπλούς λόγους από τα παραπάνω,τα
διαγράφουν ίσους διπλούς λόγους από τα παραπάνω,τα  διαγράφουν και αυτά ίσους διπλούς λόγους.Θέλουμε να δείξουμε ότι ταυτίζονται αυτά τα 3 σημεία,οπότε αρκεί να δειχτεί ότι ταυτίζονται για 3 θέσεις,αφού μετά κατασκευάζονται μονοσήμαντα οι υπόλοιπες θέσεις ώστε κάθε τετράδα να έχει ίσο διπλό λόγο με τις άλλες.Με απλό έλεγχο θέσης (για
διαγράφουν και αυτά ίσους διπλούς λόγους.Θέλουμε να δείξουμε ότι ταυτίζονται αυτά τα 3 σημεία,οπότε αρκεί να δειχτεί ότι ταυτίζονται για 3 θέσεις,αφού μετά κατασκευάζονται μονοσήμαντα οι υπόλοιπες θέσεις ώστε κάθε τετράδα να έχει ίσο διπλό λόγο με τις άλλες.Με απλό έλεγχο θέσης (για  ),έστω
),έστω  .Από το τρίτο λήμμα,τα
.Από το τρίτο λήμμα,τα  βρίσκονται στην ίδια κωνική,όπου
βρίσκονται στην ίδια κωνική,όπου  .Από το δεύτερο λήμμα,το κέντρο της κωνικής βρίσκεται πάνω στο ποδικό του
.Από το δεύτερο λήμμα,το κέντρο της κωνικής βρίσκεται πάνω στο ποδικό του  του τριγώνου,το οποίο βρίσκεται πάνω σε αυτή την υπερβολή,ο σεβιανός του κύκλος (ο εγγεγραμμένος) τέμνει (εφάπτεται) στον κύκλο του
του τριγώνου,το οποίο βρίσκεται πάνω σε αυτή την υπερβολή,ο σεβιανός του κύκλος (ο εγγεγραμμένος) τέμνει (εφάπτεται) στον κύκλο του 
 (
( ορθόκεντρο,
ορθόκεντρο, ).
).
 ως προς την υπερβολή είναι η
ως προς την υπερβολή είναι η  (και κυκλικά τα υπόλοιπα) και του
(και κυκλικά τα υπόλοιπα) και του  η
η  .
. και ελπίζω να δείξω πως εφάπτεται και στις
και ελπίζω να δείξω πως εφάπτεται και στις  .
. τα συμμετρικά του
τα συμμετρικά του  .
. είναι ομοκυκλικές τετράδες.
είναι ομοκυκλικές τετράδες.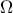 η τομή των
η τομή των  .
. .
.
 εγγράψιμα
εγγράψιμα .
. (μην ξεχνάμε άλλωστε πως το
(μην ξεχνάμε άλλωστε πως το  ανήκει τόσο στον ποδικό κύκλο του
ανήκει τόσο στον ποδικό κύκλο του  ) του
) του  (έστω
(έστω  ) περνάει από το
) περνάει από το  .Αυτό μπορούμε να το δούμε ως εξής:Το
.Αυτό μπορούμε να το δούμε ως εξής:Το  .Συνεπώς,επειδή η αντιστροφή (κέντρου
.Συνεπώς,επειδή η αντιστροφή (κέντρου  δηλαδή θα γίνει το κέντρο του κλπ.
δηλαδή θα γίνει το κέντρο του κλπ. οι δεύτερες τομές των
οι δεύτερες τομές των  ,
, ,
, και
και  τα μέσα των
τα μέσα των  .
. .
. εγγράψιμο.
εγγράψιμο. .
. φτιάχνουμε από τις τομές τους το DEF(βλ. σχήμα 2).
φτιάχνουμε από τις τομές τους το DEF(βλ. σχήμα 2). .
. .
. που περνάει από το περίκεντρο
που περνάει από το περίκεντρο  .
. το ποδικό του
το ποδικό του 
 και δείχνουμε ότι ανήκει στους
και δείχνουμε ότι ανήκει στους  .
.
 ,έστω
,έστω  συντρέχουν στον
συντρέχουν στον  σε σημείο
σε σημείο  .
. .
. αντίστοιχα λόγω συμμετρίας(σχήμα 3).
αντίστοιχα λόγω συμμετρίας(σχήμα 3). εγγράψιμο και θα έχουμε τελειώσει.
εγγράψιμο και θα έχουμε τελειώσει. και
και  και η απόδειξη έχει γίνει.
και η απόδειξη έχει γίνει. (και οι κυκλικές της),όπου
(και οι κυκλικές της),όπου  περνάει από σταθερό σημείο.
περνάει από σταθερό σημείο. η προβολή του
η προβολή του  .
. ,όσο και στον
,όσο και στον  .
. του
του  και λόγω αυτόυ ανήκει και στους
και λόγω αυτόυ ανήκει και στους  .
. είναι προβολική ως στροφή κατά σταθερή γωνία.
είναι προβολική ως στροφή κατά σταθερή γωνία. είναι επίσης προβολικές ως προβολές σε σταθερή ευθεία.
είναι επίσης προβολικές ως προβολές σε σταθερή ευθεία. .Όταν μάλιστα το
.Όταν μάλιστα το  .
. ).
). η προβολή του
η προβολή του  ,
, η τομή
η τομή  .
. είναι κάθετη στην
είναι κάθετη στην  ή κατόπιν συμμετρίας προς την
ή κατόπιν συμμετρίας προς την  ότι το συμμετρικό του
ότι το συμμετρικό του  συνευθειακά.
συνευθειακά. αρκεί
αρκεί  συνευθειακά με
συνευθειακά με  το συμμετρικό του
το συμμετρικό του  στους
στους  λαμβάνουμε πως η τομή της
λαμβάνουμε πως η τομή της  με τον κύκλο
με τον κύκλο  βρίσκεται στην εκ του
βρίσκεται στην εκ του  (
( (και των κυκλικών τους) ανήκει στον
(και των κυκλικών τους) ανήκει στον  .
.