vittasko έγραψε:ΛΗΜΜΑ. - Δίνεται παραλληλόγραμμο  και έστω
και έστω  τυχόν σημείο στο εσωτερικό του. Δια του σημείου
τυχόν σημείο στο εσωτερικό του. Δια του σημείου  φέρνουμε τις παράλληλες ευθείες προς τις
φέρνουμε τις παράλληλες ευθείες προς τις  οι οποίες τέμνουν τις
οι οποίες τέμνουν τις  στα σημεία
στα σημεία  αντιστοίχως. Αποδείξτε ότι τα σημεία
αντιστοίχως. Αποδείξτε ότι τα σημεία  είναι συνευθειακά.
είναι συνευθειακά.
Υπάρχει κάπου μία στοιχειώδης απόδειξη αυτού του
Λήμματος και ελπίζω ότι θα την βρω. (*)
Ας δούμε εδώ μία προσέγγιση βασισμένη στο
θεώρημα Πάππου.

- Η εκ του Nagel παράλληλη ευθεία στη διχοτόμο - Βοηθητική πρόταση - Απόδειξη του Λήμματος.
- f=112_t=45570(b).PNG (16.31 KiB) Προβλήθηκε 4661 φορές

Έστω τα ( κατά εκδοχήν ) σημεία
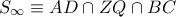
και

Επί των ευθειών

θεωρούμε τις τριάδες των σημείων

και

και σύμφωνα με το
θεώρημα Πάππου, προκύπτει ως άμεσο συμπέρασμα ότι τα σημεία

και

και

είναι συνευθειακά και το
Λήμμα έχει αποδειχθεί.
ΣΗΜΕΙΩΣΗ : Το ως άνω
Λήμμα είναι στην πραγματικότητα μία ειδική περίπτωση ενός γνωστού επίσης ως
Θεώρημα Brianchon, όπου πάλι τα σημεία

είναι συνευθειακά, αλλά το

είναι τυχόν τετράπλευρο, με το

τυχόν σημείο στο εσωτερικό του και τα σημεία
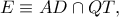
και
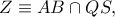
όπου

και

και

.

- Η εκ του Nagel παράλληλη στην διχοτόμο - Γενίκευση του Λήμματος γνωστή ως θεώρημα Brianchon.
- f=112_t=45570(c).PNG (16.79 KiB) Προβλήθηκε 4651 φορές
Το ως άνω
Θεώρημα Brianchon, αποδεικνύεται ομοίως, ως άμεσο συμπέρασμα του
Θεωρήματος Πάππου, θεωρώντας τις τριάδες των σημείων

και

επί των ευθειών

αντιστοίχως ( Δ.Γ. ΚΟΝΤΟΓΙΑΝΝΗΣ - Mαθηματικές Ολυμπιάδες - ΓΕΩΜΕΤΡΙΑ 1 , Σελίδα 177 - Αυτοέκδοση , Αθήνα 1987 ).
Κώστας Βήττας.
(*) (19-03-2016) - Δείτε
Εδώ .
 , όπου
, όπου  το συμμετρικό του μέσου
το συμμετρικό του μέσου  του τόξου
του τόξου  του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου  που δεν περιέχει
που δεν περιέχει  ως προς την
ως προς την  και
και  το σημείο
το σημείο 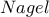 του τριγώνου
του τριγώνου  .
.
 Έστω
Έστω  τα σημεία επαφής του εγγεγραμμένου κύκλου
τα σημεία επαφής του εγγεγραμμένου κύκλου  του δοσμένου τριγώνου
του δοσμένου τριγώνου  και
και  αντιστοίχως.
αντιστοίχως.


 προκύπτει ότι το
προκύπτει ότι το  ανήκει στην παράλληλη ευθεία προς την διχοτόμο της γωνίας
ανήκει στην παράλληλη ευθεία προς την διχοτόμο της γωνίας 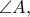 από το σημείο έστω
από το σημείο έστω  , ώστε το
, ώστε το  να είναι παραλληλόγραμμο
να είναι παραλληλόγραμμο  γνωστό αποτέλεσμα για κάθε ζεύγος σημείων
γνωστό αποτέλεσμα για κάθε ζεύγος σημείων  επί των
επί των  αντιστοίχως για τα οποία ισχύει η
αντιστοίχως για τα οποία ισχύει η  .
. και
και  είναι συμμετρικά ως προς το μέσον της πλευράς
είναι συμμετρικά ως προς το μέσον της πλευράς  προκύπτει ότι
προκύπτει ότι 
 του περικυκλίου του τριγώνου
του περικυκλίου του τριγώνου  αντίστοιχα ως προς
αντίστοιχα ως προς  , όπου
, όπου  είναι το ορθόκεντρο και το σημείο
είναι το ορθόκεντρο και το σημείο 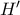 του ορθοκέντρου
του ορθοκέντρου  ως προς την
ως προς την  του τριγώνου
του τριγώνου  είναι ισοσκελές τραπέζιο (με
είναι ισοσκελές τραπέζιο (με 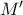 το συμμετρικό του ως προς την
το συμμετρικό του ως προς την 
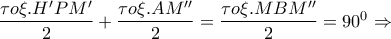

 το αντιδιαμετρικό του
το αντιδιαμετρικό του  προκύπτει ότι το
προκύπτει ότι το  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. μπορούμε να πούμε το έξής:
μπορούμε να πούμε το έξής:
 και λόγω
και λόγω  προκύπτει
προκύπτει  , δύο σημεία επί των πλευρών του
, δύο σημεία επί των πλευρών του 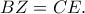 Αποδείξτε ότι το σημείο
Αποδείξτε ότι το σημείο  ανήκει στην δια του
ανήκει στην δια του  , όπου
, όπου  οι οποίες τέμνονται στο σημείο έστω
οι οποίες τέμνονται στο σημείο έστω  και έστω τα σημεία
και έστω τα σημεία  και
και 
 και
και  και
και  προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι ρόμβος και άρα έχουμε ότι η ευθεία
είναι ρόμβος και άρα έχουμε ότι η ευθεία  διχοτομεί την γωνία
διχοτομεί την γωνία  και λόγω του παραλληλογράμμου
και λόγω του παραλληλογράμμου 
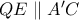 και
και 

 και
και  και έστω
και έστω  τυχόν σημείο στο εσωτερικό του. Δια του σημείου
τυχόν σημείο στο εσωτερικό του. Δια του σημείου  οι οποίες τέμνουν τις
οι οποίες τέμνουν τις  στα σημεία
στα σημεία  είναι συνευθειακά.
είναι συνευθειακά.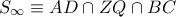 και
και 
 και
και  και σύμφωνα με το
και σύμφωνα με το  και
και  και
και  είναι συνευθειακά και το
είναι συνευθειακά και το  είναι συνευθειακά, αλλά το
είναι συνευθειακά, αλλά το 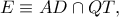 και
και 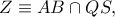 όπου
όπου  και
και  και
και  και
και  επί των ευθειών
επί των ευθειών  . Επίσης θεωρούμε
. Επίσης θεωρούμε  τα μέσα των τμημάτων
τα μέσα των τμημάτων  .
. ( εφόσον
( εφόσον  ). Επιπλέον
). Επιπλέον  ( ενώνει μέσα στο τρίγωνο
( ενώνει μέσα στο τρίγωνο  ). Επομένως, τα σημεία
). Επομένως, τα σημεία  ( απ' το τρίγωνο
( απ' το τρίγωνο  ) και αφετέρου
) και αφετέρου 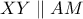 ( απ' τη συνεθειακότητα
( απ' τη συνεθειακότητα  το σημείο τομής της εκ του
το σημείο τομής της εκ του  παραλλήλου προς την
παραλλήλου προς την  με την πλευρά
με την πλευρά  του παραλληλογράμμου
του παραλληλογράμμου  . Τότε
. Τότε  προφανώς παραλληλόγραμμο
προφανώς παραλληλόγραμμο  ) και με
) και με 
 ,
, η διχοτόμος της γωνίας
η διχοτόμος της γωνίας  .
. 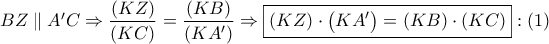 και με
και με . Από
. Από 
 και η βοηθητική πρόταση έχει αποδειχθεί.
και η βοηθητική πρόταση έχει αποδειχθεί. είναι η διχοτόμος της
είναι η διχοτόμος της  , ή ισοδύναμα, ότι οι αποστάσεις
, ή ισοδύναμα, ότι οι αποστάσεις  από τις πλευρές
από τις πλευρές  αντίστοιχα είναι ίσες.
αντίστοιχα είναι ίσες. . Τότε τα ορθ. τρίγωνα
. Τότε τα ορθ. τρίγωνα  είναι όμοια , όπως και τα ορθ.
είναι όμοια , όπως και τα ορθ. 
 και
και 

 .
. 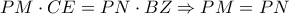 και το ζητούμενο αποδείχθηκε.
και το ζητούμενο αποδείχθηκε. και
και  .
.  τέμνονται στο
τέμνονται στο  .
. και
και  έχουμε
έχουμε 
 .
.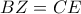 , τότε και
, τότε και  δηλ η
δηλ η