Ορθογώνιο τρίγωνο και καθετότητα

#1

Στο παρακάτω σχήμα να αποδειχθεί ότι $FZ\perp BD$ .

Κάτι μου θυμίζει(δεν έχω λύση) , αλλά δεν το βρίσκω !

#2

Μπάμπης Στεργίου έγραψε:Στο παρακάτω σχήμα να αποδειχθεί ότι $FZ\perp BD$ .Κάτι μου θυμίζει(δεν έχω λύση) , αλλά δεν το βρίσκω !

Μπάμπη καλημέρα!!. Για να σε καλοπιάσω , μπας και έρθεις "βόρεια" . Τα καλαμπόκια νομίζω πρέπει να τελειώνουν όπου νάναι

$\bullet$ Έστω $K \equiv EF \cap CA$ . Τότε από το πλήρες τετράπλευρο προκύπτει ότι οι σειρές $\left( {K,S,D,C} \right)$ και $\left( {B,Z,Q,S} \right)$ είναι αρμονικές (κάθε διαγώνιος πλήρους

τετραπλεύρου διαιρείται αρμονικά από τις άλλες δύο), όπου $Q \equiv BZ \cap PE,S \equiv BZ \cap DC$ , οπότε και οι δέσμες και είναι αρμονικές.

Προφανώς το είναι το έγκεντρο του τριγώνου $\vartriangle BDC$ (αφού διχοτόμοι των γωνιών του $\angle BDC,\angle BCD$ αντίστοιχα) και συνεπώς

η είναι η τρίτη διχοτόμος του, οπότε από την αρμονική δέσμη προκύπτει ότι $BK \bot BS \Rightarrow \vartriangle KBS$ ορθογώνιο στο .
[attachment=0]1.png[/attachment]
$\bullet$ Επίσης $\angle BSA\mathop = \limits^{\varepsilon \xi \omega \tau \varepsilon \rho \iota \kappa \eta \,\,\sigma \tau o\,\,\vartriangle BSC} \angle C + \angle SBC$ $\mathop = \limits^{\angle C = \angle ABD\,\,(o\xi \varepsilon \iota \varepsilon \varsigma \,\,\mu \varepsilon \,\,\kappa \alpha \theta \varepsilon \tau \varepsilon \varsigma \,\,\pi \lambda \varepsilon \upsilon \rho \varepsilon \varsigma ),\angle SBC = \angle SBD(\alpha \pi o\,\,\tau \eta \,\,\delta \iota \chi o\tau o\mu o)}$ $\angle ABD + \angle SBC = \angle ABS \Rightarrow \vartriangle ABS$

ισοσκελές και με το τρίγωνο $\vartriangle KBS$ ορθογώνιο στο $B \Rightarrow BA$ διάμεσος του $\vartriangle KBS$ .

Οι ακτίνες της αρμονικής δέσμης τέμνουν την ευθεία στα σημεία αντίστοιχα και με το μέσο της προκύπτει ότι η τέταρτη ακτίνας της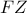

θα είναι παράλληλη προς την , δηλαδή $FZ\parallel KC\mathop \Rightarrow \limits^{BD \bot KC} \boxed{FZ \bot KC}$ και το ζητούμενο έχει αποδειχθεί.

Στάθης

#3

Μπάμπης Στεργίου έγραψε:Στο παρακάτω σχήμα να αποδειχθεί ότι $FZ\perp BD$ .

Κάτι μου θυμίζει(δεν έχω λύση) , αλλά δεν το βρίσκω !

: Ορθογώνιο και καθετότητα.png (30.54 KiB) Προβλήθηκε 1482 φορές

Καλημέρα σε όλους . Ας το δούμε και ως επί το πλείστον μετρικά
Θα μου επιτρέψει Ο Μπάμπης εναλλάξω τα σημεία A,B

για ευχρηστία γνωστών τύπων. Έστω

το σημείο τομής της

με την

και

το αρμονικό συζυγές του ως προς τα D,C

. Θα ισχύουν :

$\widehat {SAH} = {90^0}$ και τα σημεία S,P,E

συνευθειακά .Δηλαδή τα σημεία S,F,E

συνευθειακά.

Επίσης $\widehat \phi = {\widehat \phi _1}\,\,\kappa \alpha \iota \,\,\widehat \omega = {\widehat \omega _1}$ κάθετες πλευρές , άρα ${\widehat \omega _1} = {\widehat \phi _1} \Leftrightarrow AB = BS$ δηλαδή $\boxed{x = c}$

Από το θεώρημα του Μενελάου στο τρίγωνο ABC

με διατέμνουσα την SFE

έχουμε:

$\dfrac{{AF}}{{FB}} \cdot \dfrac{{BS}}{{SB}} \cdot \dfrac{{CE}}{{EA}} = 1$ . Αλλά από το θεώρημα διχοτόμων στο τρίγωνο ADC

και τις

γνωστές σχέσεις στο ορθογώνιο τρίγωνο ABC

έχουμε :

$\boxed{\dfrac{{CE}}{{EA}} = \dfrac{{DC}}{{DA}} = \dfrac{{\dfrac{{{b^2}}}{a}}}{{{\upsilon _a}}} = \dfrac{{{b^2}}}{{a{\upsilon _a}}} = \dfrac{{{b^2}}}{{bc}} = \dfrac{b}{c}}$ και άρα η προηγούμενη σχέση δίδει :

$\dfrac{{AF}}{{FB}} \cdot \dfrac{c}{{a + c}} \cdot \dfrac{b}{c} = 1 \Rightarrow \boxed{\dfrac{{AF}}{{FB}} = \dfrac{{a + c}}{b}}\,\,(1)$ . Επίσης πάλι από το θεώρημα της διχοτόμου

στο τρίγωνο ADC

έχουμε:

$\boxed{\dfrac{{AZ}}{{ZH}} = \dfrac{{AD}}{{DH}} = \dfrac{{AD}}{{\dfrac{{DC \cdot DA}}{{AD + AC}}}} = \dfrac{{AD + AC}}{{DC}} = \dfrac{{{\upsilon _a} + b}}{{\dfrac{{{b^2}}}{a}}} = \dfrac{{a{\upsilon _a} + {b^2}}}{{{b^2}}} = \dfrac{{bc + ba}}{{{b^2}}}}$ δηλαδή

$\boxed{\dfrac{{AZ}}{{ZH}} = \dfrac{{a + c}}{b}}\,\,(2)$ . Από τις $(1)\,\kappa \alpha \iota \,\,(2)$ έχουμε $\dfrac{{AF}}{{FB}} = \dfrac{{AZ}}{{ZH}}$ και άρα FZ//BC

και

αφού $AD \bot BC$ θα είναι $AD \bot FZ$

Φιλικά Νίκος

#4

Την είδα συμπτωματικά, ανεβάζοντας αυτήν (που είχε παρόμοιο τίτλο).

Στη συνέχεια ανέβασα μία γενίκευσή της εδώ και τέλος, ο Στάθης έθεσε στην ίδια άσκηση το γενικότερο πρόβλημα.

Και στις δύο περιπτώσεις λύτες οι συνήθεις ύποπτοι Νίκος Φραγκάκης και Στάθης Κούτρας

Ορθογώνιο τρίγωνο και καθετότητα

Ορθογώνιο τρίγωνο και καθετότητα

Re: Ορθογώνιο τρίγωνο και καθετότητα

Re: Ορθογώνιο τρίγωνο και καθετότητα

Re: Ορθογώνιο τρίγωνο και καθετότητα

Μέλη σε σύνδεση