 το κέντρο του εγγεγραμμένου κύκλου και
το κέντρο του εγγεγραμμένου κύκλου και  διάμετρος του περιγεγραμμένου κύκλου τριγώνου
διάμετρος του περιγεγραμμένου κύκλου τριγώνου 
Τα σημεία
 και
και  ανήκουν στις ευθείες
ανήκουν στις ευθείες  και
και  ώστε
ώστε 
Δείξτε ότι οι ευθείες
 και
και  είναι κάθετες.
είναι κάθετες.Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
 το κέντρο του εγγεγραμμένου κύκλου και
το κέντρο του εγγεγραμμένου κύκλου και  διάμετρος του περιγεγραμμένου κύκλου τριγώνου
διάμετρος του περιγεγραμμένου κύκλου τριγώνου 
 και
και  ανήκουν στις ευθείες
ανήκουν στις ευθείες  και
και  ώστε
ώστε 
 και
και  είναι κάθετες.
είναι κάθετες.socrates έγραψε:Έστωτο κέντρο του εγγεγραμμένου κύκλου και
διάμετρος του περιγεγραμμένου κύκλου τριγώνου

Τα σημείακαι
ανήκουν στις ευθείες
και
ώστε
Δείξτε ότι οι ευθείεςκαι
είναι κάθετες.
 Τα σημεία
Τα σημεία  επί των προεκτάσεων των
επί των προεκτάσεων των  προς το μέρος του
προς το μέρος του  αντιστοίχως, όπως ορίζονται στην εκφώνηση, προφανώς ταυτίζονται με τα σημεία επαφής των παρεγγεγραμμένων κύκλων
αντιστοίχως, όπως ορίζονται στην εκφώνηση, προφανώς ταυτίζονται με τα σημεία επαφής των παρεγγεγραμμένων κύκλων  αντιστοίχως, στις ίδιες ευθείες.
αντιστοίχως, στις ίδιες ευθείες.  τα σημεία επαφής του εγγεγραμμένου κύκλου
τα σημεία επαφής του εγγεγραμμένου κύκλου  του δοσμένου τριγώνου
του δοσμένου τριγώνου  στις πλευρές του
στις πλευρές του  αντιστοίχως και ας είναι
αντιστοίχως και ας είναι  τα σημεία επαφής στις ίδιες πλευρές, των κύκλων
τα σημεία επαφής στις ίδιες πλευρές, των κύκλων  αντιστοίχως.
αντιστοίχως. τα μέσα των πλευρών
τα μέσα των πλευρών  αντιστοίχως, τα οποία ταυτίζονται ως γνωστό, με τα μέσα των
αντιστοίχως, τα οποία ταυτίζονται ως γνωστό, με τα μέσα των 
 Έστω το σημείο
Έστω το σημείο  και σύμφωνα με το παρακάτω Λήμμα, έχουμε ότι
και σύμφωνα με το παρακάτω Λήμμα, έχουμε ότι 
 και
και  και
και  και
και 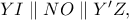 σύμφωνα με το Θεώρημα των αναλόγων διαιρέσεων, προκύπτει ότι τα σημεία
σύμφωνα με το Θεώρημα των αναλόγων διαιρέσεων, προκύπτει ότι τα σημεία  είναι συνευθειακά και ισχύει
είναι συνευθειακά και ισχύει 
 και
και 




 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. και έστω
και έστω  τα σημεία επαφής των παρεγγεγραμμένων κύκλων του
τα σημεία επαφής των παρεγγεγραμμένων κύκλων του  στις ευθείες
στις ευθείες  αντιστοίχως. Οι κύκλοι
αντιστοίχως. Οι κύκλοι  εφάπτονται στι πλευρές
εφάπτονται στι πλευρές  στα σημεία
στα σημεία  αντιστοίχως και έστω το σημείο
αντιστοίχως και έστω το σημείο  όπου
όπου  είναι αντιστοίχως, τα κέντρα των κύκλων
είναι αντιστοίχως, τα κέντρα των κύκλων  . Αποδείξτε ότι
. Αποδείξτε ότι 
vittasko έγραψε:ΛΗΜΜΑ. - Δίνεται τρίγωνοκαι έστω
τα σημεία επαφής των παρεγγεγραμμένων κύκλων του
στις ευθείες
αντιστοίχως. Οι κύκλοι
εφάπτονται στι πλευρές
στα σημεία
αντιστοίχως και έστω το σημείο
όπου
είναι αντιστοίχως, τα κέντρα των κύκλων
. Αποδείξτε ότι
 Γράφουμε τους κύκλους
Γράφουμε τους κύκλους  με διάμετρο
με διάμετρο 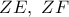 αντιστοίχως, οι οποίοι τέμνονται στο σημείο έστω
αντιστοίχως, οι οποίοι τέμνονται στο σημείο έστω  και εύκολα προκύπτει ότι τα σημεία
και εύκολα προκύπτει ότι τα σημεία  είναι συνευθειακά από
είναι συνευθειακά από  και
και  .
. και αρκεί να αποδειχθεί ότι η ευθεία
και αρκεί να αποδειχθεί ότι η ευθεία  περνάει από το
περνάει από το 
 και
και  προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι ισοσκελές τραπέζιο και άρα έγγράψιμο σε κύκλο έστω
είναι ισοσκελές τραπέζιο και άρα έγγράψιμο σε κύκλο έστω 
 ως ο ριζικός άξονας των κύκλων
ως ο ριζικός άξονας των κύκλων  περνάει από το σημείο
περνάει από το σημείο  ως το ριζικό κέντρο των κύκλων
ως το ριζικό κέντρο των κύκλων 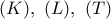 , λόγω
, λόγω  και
και  και το Λήμμα έχει αποδειχθεί.
και το Λήμμα έχει αποδειχθεί.Μόνο για λόγους πλουραλισμού και απλά να θυμηθούμε νομίζω ένα ενδιαφέρον λήμμα καθετότητας. Ανsocrates έγραψε:Έστωτο κέντρο του εγγεγραμμένου κύκλου και
διάμετρος του περιγεγραμμένου κύκλου τριγώνου
Τα σημεία
και
ανήκουν στις ευθείες
και
ώστε
. Δείξτε ότι οι ευθείες
και
είναι κάθετες.
 είναι τα σημεία επαφής του έγκυκλου
είναι τα σημεία επαφής του έγκυκλου  του τριγώνου
του τριγώνου  με τις πλευρές
με τις πλευρές  αντίστοιχα, τότε με
αντίστοιχα, τότε με  διάμετρο του περικυκλίου του οι
διάμετρο του περικυκλίου του οι  είναι οι (ορθές) προβολές του τμήματος
είναι οι (ορθές) προβολές του τμήματος  επί των ευθειών
επί των ευθειών  αντίστοιχα και ισχύει:
αντίστοιχα και ισχύει: 
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. Με την ευκαιρία του προβλήματος που έχει τεθεί από τον socrates, ας δούμε μία εναλλακτική προσέγγιση του Λήμματος στο οποίο αναφέρθηκε ο φίλτατος Στάθης, το οποίο έχει πράγματι ενδιαφέρον ως θεώρημα και καλό είναι να το έχουμε υπόψη μας, αφού κάποιες αποδείξεις καλή ώρα όπως εδώ, απλουστεύονται ως άμεσες εφαρμογές του.
Με την ευκαιρία του προβλήματος που έχει τεθεί από τον socrates, ας δούμε μία εναλλακτική προσέγγιση του Λήμματος στο οποίο αναφέρθηκε ο φίλτατος Στάθης, το οποίο έχει πράγματι ενδιαφέρον ως θεώρημα και καλό είναι να το έχουμε υπόψη μας, αφού κάποιες αποδείξεις καλή ώρα όπως εδώ, απλουστεύονται ως άμεσες εφαρμογές του. Θα αποδείξουμε πρώτα την ακόλουθη Βοηθητική πρόταση, ειδική περίπτωση του ως άνω θεωρήματος.ΘΕΩΡΗΜΑ ΤΩΝ ΚΑΘΕΤΩΝ ΕΥΘΕΙΩΝ. - Δίνεται γωνίακαι έστω
τυχόντα σημεία στο εσωτερικό της. Έστω
οι προβολές των
αντιστοίχως επί της
και έστω
οι προβολές των επί της
, αντιστοίχως. Επί των
ή επί των προεκτάσεών τους προς το μέρος του
θεωρούμε τα σημεία
αντιστοίχως, ώστε να είναι
. Αποδείξτε ότι
 δοσμένου τριγώνου
δοσμένου τριγώνου  , προς το μέρος των
, προς το μέρος των  λαμβάνουμε τα σημεία
λαμβάνουμε τα σημεία  αντιστοίχως, ώστε να είναι
αντιστοίχως, ώστε να είναι  . Οι δια των
. Οι δια των  κάθετες ευθείες επί των
κάθετες ευθείες επί των  αντιστοίχως, τέμνονται στο σημείο έστω
αντιστοίχως, τέμνονται στο σημείο έστω  και ας είναι
και ας είναι  το σημείο τομής των δια των
το σημείο τομής των δια των  καθέτων ευθειών επί των
καθέτων ευθειών επί των  αντιστοίχως. Αποδείξτε ότι
αντιστοίχως. Αποδείξτε ότι  Απόδειξη της Βοηθητικής πρότασης. Έστω
Απόδειξη της Βοηθητικής πρότασης. Έστω  οι προβολές του σημείου
οι προβολές του σημείου  επί των
επί των  αντιστοίχως και
αντιστοίχως και  και
και  , έχουμε
, έχουμε 
 λόγω
λόγω 


 και από
και από  λόγω του εγραψίμου τετραπλεύρου
λόγω του εγραψίμου τετραπλεύρου 

 συμπεραίνεται ότι το τετράπλευρο
συμπεραίνεται ότι το τετράπλευρο  όπου
όπου  είναι εγγράψιμο και άρα,
είναι εγγράψιμο και άρα, 

 και η Βοηθητική πρόταση έχει αποδειχθεί.
και η Βοηθητική πρόταση έχει αποδειχθεί. Μία άλλη απόδειξη της Βοηθητικής πρότασης, της οποίας ισχύει και το αντίστροφο, βασισμένη στο Πυθαγόρειο Θεώρημα, αφήνεται στον αναγνώστη ως άσκηση.
Μία άλλη απόδειξη της Βοηθητικής πρότασης, της οποίας ισχύει και το αντίστροφο, βασισμένη στο Πυθαγόρειο Θεώρημα, αφήνεται στον αναγνώστη ως άσκηση. το σημείο επί της
το σημείο επί της  ώστε να είναι
ώστε να είναι  και ας είναι
και ας είναι 
 αντιστοίχως, ώστε να είναι
αντιστοίχως, ώστε να είναι  και
και  και
και 






 και
και 


 , σύμφωνα με την Βοηθητική πρόταση, έχουμε
, σύμφωνα με την Βοηθητική πρόταση, έχουμε 
 και
και  και
και  συμπεραίνεται ότι
συμπεραίνεται ότι  και το Θεώρημα των καθέτων ευθειών ( ή θεώρημα Κούτρα ), έχει αποδειχθεί.
και το Θεώρημα των καθέτων ευθειών ( ή θεώρημα Κούτρα ), έχει αποδειχθεί....Θεώρημα των καθέτων ευθειών ( ή θεώρημα Κούτρα ), έχει αποδειχθεί.vittasko έγραψε:ΘΕΩΡΗΜΑ ΤΩΝ ΚΑΘΕΤΩΝ ΕΥΘΕΙΩΝ. - Δίνεται γωνίακαι έστω
τυχόντα σημεία στο εσωτερικό της. Έστω
οι προβολές των
αντιστοίχως επί της
και έστω
οι προβολές των επί της
, αντιστοίχως. Επί των
ή επί των προεκτάσεών τους προς το μέρος του
θεωρούμε τα σημεία
αντιστοίχως, ώστε να είναι
. Αποδείξτε ότι
 το σημείο τομής δύο ευθειών
το σημείο τομής δύο ευθειών  και ας είναι
και ας είναι  και
και  εκατέρωθεν του
εκατέρωθεν του  όπως φαίνεται στο σχήμα και έστω
όπως φαίνεται στο σχήμα και έστω 
 καθέτων ευθειών επί των
καθέτων ευθειών επί των  αντίστοιχα. Να δειχθεί ότι
αντίστοιχα. Να δειχθεί ότι  Η απόδειξη είναι απλή... Από την προφανή ισότητα (Π – Γ – Π) των τριγώνων
Η απόδειξη είναι απλή... Από την προφανή ισότητα (Π – Γ – Π) των τριγώνων  .
.  οδηγεί στο να είναι
οδηγεί στο να είναι 
 , οπότε
, οπότε 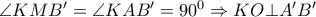 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. μεταφερθεί παράλληλα προς τον εαυτό του διατηρώντας το μήκος του (ας πούμε) στη θέση
μεταφερθεί παράλληλα προς τον εαυτό του διατηρώντας το μήκος του (ας πούμε) στη θέση  τότε προφανώς ισχύει:
τότε προφανώς ισχύει:  , με
, με  τις ορθές προβολές του
τις ορθές προβολές του  στις
στις  αντίστοιχα, και αν
αντίστοιχα, και αν  μεταφερθεί παράλληλα
μεταφερθεί παράλληλα  (μέσω της αναλογίας
(μέσω της αναλογίας  )
) ως παράλληλα αντίστοιχα στα μεταξύ τους κάθετα τμήματα
ως παράλληλα αντίστοιχα στα μεταξύ τους κάθετα τμήματα  και
και  .
. είναι οι ορθές προβολές του
είναι οι ορθές προβολές του  στις
στις  αντίστοιχα.
αντίστοιχα. . Θ.δ.ο
. Θ.δ.ο  . Φέρω
. Φέρω  οπότε
οπότε  .
.  (οξείες με
(οξείες με  πλευρές) άρα
πλευρές) άρα  (Ν. Ημιτόνων).
(Ν. Ημιτόνων). Θ.δ.ο
Θ.δ.ο  . Έχουμε όπως πριν
. Έχουμε όπως πριν  και
και 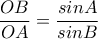 άρα
άρα 
 και
και 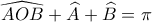 έπεται
έπεται  .
. . Τότε (βλ. σχήμα)
. Τότε (βλ. σχήμα)  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες