Μια λίγο διαφορετική λύση.
Έστω

το σημείο τομής της

με την

και

το σημείο τομής της

με την

.
Είναι γνωστό πως η δέσμη
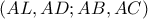
είναι αρμονική.Τώρα αν την τμήσουμε με την

προκύπτει πως και η δέσμη
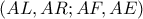
είναι αρμονική άρα και η σημειοσειρά
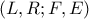
θα είναι αρμονική. Κατά συνέπεια η δέσμη
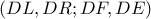
είναι αρμονική.Τεμνοντάς την με την

και δεδομένου ότι θέλουμε το

να είναι το μέσο το

προκύπτει πως αρκεί να αποδείξουμε ότι
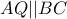
.
Διαφορετικά αρκεί να αποδείξουμε ότι η παράλληλη στη

από το

, η

και η
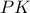
συντρέχουν, όπου

το σημείο τομής της

με τον εγγεγραμμένο κύκλο.
Αφού
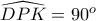
, έχουμε ότι τα σημεία
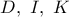
είναι συνευθειακά. Έστω ότι η ευθεία που περνά από τα
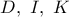
τέμνει την

στο

, όπου

η παράλληλη από το

στη

.
Έτσι
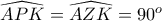
, άρα το τετράπλευρο
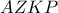
είναι εγγράψιμο.
Επιπλέον
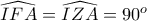
, επομένως το

ανήκει στον περιγεγραμμένο κύκλο του τριγώνου
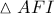
(

έκκεντρο ). Όμως είναι γνωστό πως το τετράπλευρο

είναι εγγράψιμο, με αποτέλεσμα τα σημεία

να είναι ομοκυκλικά.
Τώρα το ζητούμενο έπεται άμεσα καθώς η ευθείες
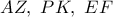
συντρέχουν στο ριζικό κέντρο των
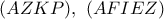
και του εγγεγραμμένου κύκλου του τριγώνου.
 με
με  Ο εγγεγραμμένος κύκλος
Ο εγγεγραμμένος κύκλος  του τριγώνου
του τριγώνου  εφάπτεται στις πλευρές
εφάπτεται στις πλευρές  στα σημεία
στα σημεία 
 τέμνει τον κύκλο
τέμνει τον κύκλο  για δεύτερη φορά στο
για δεύτερη φορά στο  Έστω
Έστω  το σημείο τομής της
το σημείο τομής της  με την κάθετη στην
με την κάθετη στην  στο
στο 
 τα σημεία τομής της
τα σημεία τομής της  με την
με την  και την
και την  αντίστοιχα.
αντίστοιχα. είναι το μέσο του τμήματος
είναι το μέσο του τμήματος 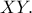

 το αντιδιαμετρικό του
το αντιδιαμετρικό του  στον
στον  και
και 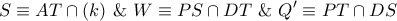 .
. είναι η πολική του
είναι η πολική του  άρα αφού
άρα αφού 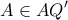 τότε από το Θ. La Hire το
τότε από το Θ. La Hire το  δηλαδή
δηλαδή  .
.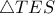 και
και 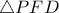 ως προς το κέντρο
ως προς το κέντρο  συντρέχουν άρα
συντρέχουν άρα 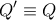 .
. το
το 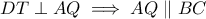 . Επίσης οι
. Επίσης οι  συντρέχουν στο σημείο Gergonne
συντρέχουν στο σημείο Gergonne  .
.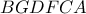 προκύπτει ότι η δέσμη
προκύπτει ότι η δέσμη 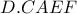 είναι αρμονική άρα η δέσμη
είναι αρμονική άρα η δέσμη 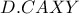 είναι επίσης αρμονική.
είναι επίσης αρμονική. η
η 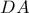 διχοτομεί το τμήμα
διχοτομεί το τμήμα 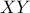 .
. το έγκεντρο του
το έγκεντρο του  και
και 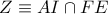 . Εφόσον
. Εφόσον  χαρταετός θα είναι
χαρταετός θα είναι 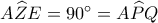 και το τετράπλευρο
και το τετράπλευρο  εγγράψιμο.
εγγράψιμο.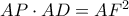 και απ’ την ομοιότητα των
και απ’ την ομοιότητα των  . Έτσι,
. Έτσι, 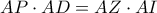 και το τετράπλευρο
και το τετράπλευρο 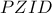 είναι εγγράψιμο (Υπάρχει και
είναι εγγράψιμο (Υπάρχει και 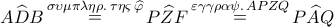 , που σημαίνει
, που σημαίνει 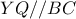 . Έτσι απ’ τα ισοσκελή (λόγω εφαπτόμενων τμημάτων)
. Έτσι απ’ τα ισοσκελή (λόγω εφαπτόμενων τμημάτων)  προκύπτουν τα αντίστοιχα όμοια ισοσκελή
προκύπτουν τα αντίστοιχα όμοια ισοσκελή  και εφόσον
και εφόσον  , έπεται
, έπεται 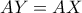 .
. το σημείο τομής της
το σημείο τομής της  με την
με την  το σημείο τομής της
το σημείο τομής της  με την
με την 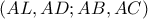 είναι αρμονική.Τώρα αν την τμήσουμε με την
είναι αρμονική.Τώρα αν την τμήσουμε με την 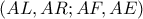 είναι αρμονική άρα και η σημειοσειρά
είναι αρμονική άρα και η σημειοσειρά 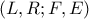 θα είναι αρμονική. Κατά συνέπεια η δέσμη
θα είναι αρμονική. Κατά συνέπεια η δέσμη 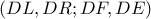 είναι αρμονική.Τεμνοντάς την με την
είναι αρμονική.Τεμνοντάς την με την  και δεδομένου ότι θέλουμε το
και δεδομένου ότι θέλουμε το 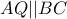 .
.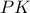 συντρέχουν, όπου
συντρέχουν, όπου  το σημείο τομής της
το σημείο τομής της  με τον εγγεγραμμένο κύκλο.
με τον εγγεγραμμένο κύκλο.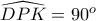 , έχουμε ότι τα σημεία
, έχουμε ότι τα σημεία 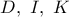 είναι συνευθειακά. Έστω ότι η ευθεία που περνά από τα
είναι συνευθειακά. Έστω ότι η ευθεία που περνά από τα  στο
στο  , όπου
, όπου 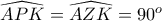 , άρα το τετράπλευρο
, άρα το τετράπλευρο 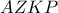 είναι εγγράψιμο.
είναι εγγράψιμο.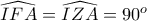 , επομένως το
, επομένως το 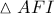 (
(  να είναι ομοκυκλικά.
να είναι ομοκυκλικά.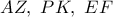 συντρέχουν στο ριζικό κέντρο των
συντρέχουν στο ριζικό κέντρο των 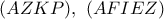 και του εγγεγραμμένου κύκλου του τριγώνου.
και του εγγεγραμμένου κύκλου του τριγώνου.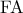 συμμετροδιάμεσος στο
συμμετροδιάμεσος στο 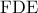 οπότε
οπότε  αρμονικό.Έτσι αν
αρμονικό.Έτσι αν 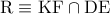 (όπου
(όπου  ) θα είναι
) θα είναι  επειδή
επειδή  .
. είναι στην πολική του
είναι στην πολική του  και επειδή είναι και στην πολική του
και επειδή είναι και στην πολική του  έπεται ότι ο πόλος της
έπεται ότι ο πόλος της 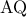 είναι το
είναι το  οπότε αφού
οπότε αφού 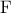 πόλος της
πόλος της  θα είναι
θα είναι 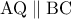 .
.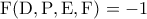 (
(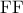 η εφαπτομένη στο
η εφαπτομένη στο  είναι στην πολική του
είναι στην πολική του  φέρεις τυχαία τέμνουσα
φέρεις τυχαία τέμνουσα 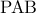 σε κύκλο η οποία τέμνει την πολική του
σε κύκλο η οποία τέμνει την πολική του 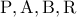 σχηματίζουν αρμονική τετράδα.
σχηματίζουν αρμονική τετράδα.