Σελίδα 1 από 1
Ωραία γεωμετρία !
Δημοσιεύτηκε: Τετ Οκτ 14, 2009 7:47 pm
από Μπάμπης Στεργίου
Μετά τη σχετική υπόδειξη και το σχήμα η άσκηση γίνεται πιο ανθρώπινη. Αν βρείτε και άλλη λύση, ας την γράψετε. Ετοιμάζω τον τόμο 1 , οπότε ας μη μείνει έξω τίποτα το εξαιρετικό .
Την άσκηση την έχω στο συνημμένο.
Μπάμπης
Re: Ωραία γεωμετρία !
Δημοσιεύτηκε: Τετ Οκτ 14, 2009 9:30 pm
από Φωτεινή
καλησπέρα
Μπάμπη ,νομίζω πως το απέδειξα
δεν έχω σχήμα όμως ,γράφω τις γωνίες με τρία γράμματα-λίγο κουραστικό-και εννοείται πως δεν τις συμβολίζω !!!
σημειώστε στο σχήμα σας και θα τα βρείτε
λοιπόν πάμε
----------------
Προεκτείνω την ΑΜ προς το Μ, έστω ΜΧ ημιευθεία
1) ΧΜΒ=Γ …… (ΜΑΓΒ εγράψιμο)
2) ΔΜΕ=Α,(ΔΜΑΕ)
3)ΑΜΕ=ΑΔΕ=Γ…..(ΑΜΔΕ,…ΔΕΓΒ, ΕΓΡΑΨΙΜΑ)
4)αρκει να δείξω ότι ΝΜΔ+ΔΜΕ+ΕΜΑ+ΜΝΕ=180
δηλαδή ΝΜΔ= Β-Γ
5)ΜΔΑ= ΝΜΔ+ ΜΒΔ (Εξωτερική ΤΟΥ ,ΜΒΔ)
6)ΜΑΔ=ΜΕΔ….(ΜΑΕΓ----εγράψιμο)
8)ΑΕΔ=Β….(ΔΕΓΒ---εγράψιμο)
9)ΑΕΜ=ΑΔΜ=Β-ΜΑΔ
10)ΜΕΝ=ΝΒΓ=>Επομένως=>ΔΕΝ=ΝΒΔ
11)άρα ΜΕΝ=ΜΕΔ+ΔΕΝ=ΜΑΔ+ΝΒΑ=ΧΜΒ=Γ
12)ΣΤΟ ΒΜΑ
ΝΜΔ=180-ΝΒΔ-ΔΜΕ-ΕΜΑ-ΜΑΔ=Β-Γ και αποδείχθηκε το ζητούμενο
Άρα ΜΑ//ΝΕ
Και επομένως ΑΜΕ=ΜΕΝ=Γ=ΜΝΕ===>ΜΝ=ΜΕ
ΤΕΛΟΣ (θέλω να πιστεύω πως δεν μου ξέφυγε κάτι στην αντιγραφή)
Re: Ωραία γεωμετρία !
Δημοσιεύτηκε: Πέμ Οκτ 15, 2009 3:06 am
από dimitris pap
Ωραία άσκηση που πιστεύω έχει αρκετές λύσεις!!
Μία λύση στηρίζεται στη στροφική ομοιοθεσία!
Απ' τη κατασκευή του το

είναι το κέντρο της στροφικής ομοιοθεσίας που πηγαίνει το

στο

(αφού είναι η τομή των κύκλων
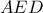
,

! (αποδεικνύεται εύκολα γωνιακά// δείτε άσκηση ΒΜΟ 2009).
Η γωνία της στροφής είναι

. Εστω τώρα

τα μέσα των

,

. Τότε η ίδια στροφική ομοιοθεσία πηγαίνει το K στο L κι έτσι

. Αυτό σημαίνει ότι

ομοκυκλικά κι αφού ο κύκλος

περνάει απ' το

έχουμε το ζητούμενο!

Χαιρετίσματα από Αγγλία
Re: Ωραία γεωμετρία !
Δημοσιεύτηκε: Πέμ Οκτ 15, 2009 3:44 pm
από S.E.Louridas
Dancing with the circles
Θεωρούμε το εγγεγραμμένο σε κύκλο κέντρου Ο τετράπλευρο BCDT , με

Εύκολα αποδεικνύεται (εξ άλλου είναι το θεώρημα του
Miquel) ότι υπάρχει μοναδικό σημείο

από το οποίο διέρχονται οι περιγραμμένοι κύκλοι στα τρίγωνα ATD ,ABC,BTS, DCS. Άμεσα έχουμε
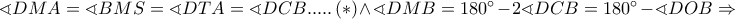

Παρατήρηση:
Στην πανέμορφη άσκηση του φίλου Μπάμπη ,προφανώς οι κοινές χορδές που υπάρχουν εδώ συντρέχουν σε ριζικό κέντρο ή
είναι παράλληλες.
S.E.Louridas
Re: Ωραία γεωμετρία !
Δημοσιεύτηκε: Πέμ Οκτ 15, 2009 9:31 pm
από Μπάμπης Στεργίου
S.E.Louridas έγραψε:Dancing with the circles
Θεωρούμε το εγγεγραμμένο σε κύκλο κέντρου Ο τετράπλευρο BCDT , με

Εύκολα αποδεικνύεται (εξ άλλου είναι το θεώρημα του
Miquel) ότι υπάρχει μοναδικό σημείο

από το οποίο διέρχονται οι περιγραμμένοι κύκλοι στα τρίγωνα ATD ,ABC,BTS, DCS. Άμεσα έχουμε
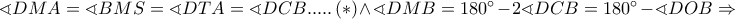

Παρατήρηση:
Στην πανέμορφη άσκηση του φίλου Μπάμπη ,προφανώς οι κοινές χορδές που υπάρχουν εδώ συντρέχουν σε ριζικό κέντρο ή
είναι παράλληλες.
S.E.Louridas
Σωτήρη, αυτή την ωραία λύση(original Louridas !) θέλω να την κουβεντιάσουμε λίγο από κοντά όταν βρεθούμε.Εϊναι πολύ ωραία και τη θέλω επώνυμα ως εφαρμογή στο θεώρημα
Miquel.
Θέλω μόνο να έχεις μαζί σου το σχήμα , διότι αυτό δεν γίνεται εύκολα χωρίς γεωμ.όργανα.
Μπάμπης
(τη λύση με το ριζικό κέντρο την έχω στο βιβλίο των ολυμπιάδων -τόμος 3)
Re: Ωραία γεωμετρία !
Δημοσιεύτηκε: Πέμ Οκτ 15, 2009 11:51 pm
από AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ
Πολύ ωραίες και οι δύο λύσεις, του Σωτήρη και του Δημήτρη να προσθέσω και μία τρίτη, αφού ευχαριστήσω τον Μπάμπη, καθώς με έκανε να την θυμηθώ (νομίζω την είχα δεί όταν πρωτοδιάβασα το βιβλίο σου και την είχα λύσει, αλλά έχω το κακό συνήθειο να μην γράφω τις λύσεις μου...)
Λύση
Αρχικά το ΑΚΟΧ είναι παραλληλόγραμμο, (αν Χ είναι το περίκεντρο του ΑΔΕ και Κ του ΑΒΓ) καθώς η ΔΕ είναι αντιπαράλληλη της ΒΓ, επομένως κάθετη στην ΑΚ και η ΑΧ κάθετη στην ΒΓ καθώς είναι ισογώνια της ΑΚ, στο τρίγωνο ΑΔΕ.
Επομένως η μεσοκάθετος της ΑΜ περνά από τα κέντρα Χ και Κ καθώς και από το μέσο της ΑΟ, δηλαδή ΟΜ//ΚΧ.
Φιλικά,
ΑΝΔΡΕΑΣ
Re: Ωραία γεωμετρία !
Δημοσιεύτηκε: Παρ Οκτ 16, 2009 1:26 pm
από hsiodos
Καλημέρα
Μια λύση ακόμα
1. Από το εγγράψιμο ΜΑΓΒ παίρνουμε

.
Από το εγγράψιμο ΔΕΓΒ παίρνουμε
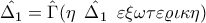
.
Από το εγγράψιμο ΜΑΕΔ παίρνουμε

. Από τις προηγούμενες σχέσεις προκύπτει

και έτσι συμπεραίνουμε ότι
η ΜΑ είναι διχοτόμος της  2.
2. Είναι
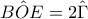
(Επίκεντρη-εγγεγραμμένη στον κύκλο (Ο)). Επίσης

Έτσι

οπότε το ΒΜΕΟ είναι εγγράψιμο.
3. Επειδή ΟΒ=ΟΕ (ακτίνες) από το εγγράψιμο ΒΜΕΟ παίρνουμε

οπότε
η ΜΟ είναι διχοτόμος της 
Τώρα από (*) και (**) προκύπτει ότι

Γιώργος
** Η άσκηση πράγματι είναι πολύ ωραία. Προσπάθησα να την λύσω χρησιμοποιώντας μόνο αρμονικές δέσμες αλλά δεν τα κατάφερα. Αν πειραματιστεί κάποιος με το σχήμα θα διαπιστώσει πολλά ενδιαφέροντα πράγματα που θα μπορούσαν να μπουν σαν ερωτήματα.
Για παράδειγμα αν ΔΕ όχι παράλληλη στην ΒΓ και Η το σημείο τομής των ΔΕ,ΒΓ παρατηρώ ότι: Η κάθετη από το Α στην ΗΟ , η ΓΔ , η ΒΕ και η ΜΟ συντρέχουν.
Μέχρι τώρα δεν έχω καταφέρει να αποδείξω γιατί η ΜΟ συντρέχει με τις άλλες τρεις.

- γεωμετρία-Μπάμπης.png (50.34 KiB) Προβλήθηκε 1033 φορές
Re: Ωραία γεωμετρία !
Δημοσιεύτηκε: Παρ Οκτ 16, 2009 4:08 pm
από dimitris pap
hsiodos έγραψε:
** Η άσκηση πράγματι είναι πολύ ωραία. Προσπάθησα να την λύσω χρησιμοποιώντας μόνο αρμονικές δέσμες αλλά δεν τα κατάφερα. Αν πειραματιστεί κάποιος με το σχήμα θα διαπιστώσει πολλά ενδιαφέροντα πράγματα που θα μπορούσαν να μπουν σαν ερωτήματα.
Για παράδειγμα αν ΔΕ όχι παράλληλη στην ΒΓ και Η το σημείο τομής των ΔΕ,ΒΓ παρατηρώ ότι: Η κάθετη από το Α στην ΗΟ , η ΓΔ , η ΒΕ και η ΜΟ συντρέχουν.
Μέχρι τώρα δεν έχω καταφέρει να αποδείξω γιατί η ΜΟ συντρέχει με τις άλλες τρεις.
-Μπάμπης.png
Αυτό προκύπτει άμεσα με χρήση πολικών! Δηλαδή έχουμε, αν Κ είναι το σημείο τομής

, ότι

είναι η πολική του

κι άρα

. Ομοια προκύπτει (και αυτό που λες) ότι Κ ορθόκεντρο του

Re: Ωραία γεωμετρία !
Δημοσιεύτηκε: Παρ Οκτ 16, 2009 4:22 pm
από vittasko
Γιώργο καλησπέρα, τι γίνεσαι ;
Η κάθετη ευθεία από το

επί την

είναι η πολική ευθεία του

ως προς τον περίκυκλο

του τετραπλεύρου

και ως γνωστό, περνάει από το σημείο
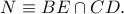
Είναι γνωστό επίσης, ότι η ευθεία που συνδέει το κένρο του

( περίκυκλου του

) με το

( σημείο τομής των διαγωνίων του

), είναι κάθετη επί την ευθεία

( που συνδέει τα σημεία τομής των απέναντι πλευρών του

) και άρα έχουμε


Όπως γράφει και ο Σωτήρης πιο πάνω, το

είναι το
σημείο Miquel στο πλήρες τετράπλευρο

και λόγω του εγγραψίμου

( ειδική περίπτωση ), κείται επί της ευθείας

Κώστας Βήττας.
Re: Ωραία γεωμετρία !
Δημοσιεύτηκε: Παρ Οκτ 16, 2009 4:58 pm
από hsiodos
Γεια σου Κώστα
Σε ευχαριστώ για τα όσα κατατοπιστικά έγραψες. Αυτό που είναι γνωστό (μπλε γράμματα) εμένα μου διέφευγε! Το σημειώνει και ο
Δημήτρης πιο πάνω τον οποίο επίσης ευχαριστώ. Που θα πάει, όσο θα περνάει ο καιρός θα εξοικειώνομαι με τις πολικές. Ας είναι καλά οι γεωμέτρες της παρέας!
Γιώργος
Re: Ωραία γεωμετρία !
Δημοσιεύτηκε: Κυρ Νοέμ 01, 2009 9:26 am
από S.E.Louridas
Επειδή μου ζητήθηκε (προσωπικά μηνύματα κ.τ.λ.) να προσαρμόσω την λύση μου στο θέμα ‘Ωραία γεωμετρία’ του Μπάμπη στο σχήμα που υπάρχει εκεί, επιτρέψτε μου να το κάνω.
Αν οι χορδές ΑΜ, ΔΕ, ΒΓ είναι παράλληλες το πρόβλημα είναι προφανές.
Αν τουλάχιστον δύο από αυτές δεν είναι παράλληλες τότε και οι τρεις συναντώνται στο ριζικό κέντρο, έστω S .Το σημείο Μ είναι το σημείο
Miquel ,τομή των περιγραμμένων κύκλων στα τρίγωνα ΔΑΕ, ΔSΒ, ΑΒΓ, SΕΓ που βρίσκεται στην ΑS, αφού το ΔΒΓΕ είναι εγγράψιμμο (ικανή και αναγκαία συνθήκη για το γεγονός αυτό).

ομοκυκλικά σημεία με ΟΕ=ΟΒ,
επομένως

S.E.Louridas
 είναι το κέντρο της στροφικής ομοιοθεσίας που πηγαίνει το
είναι το κέντρο της στροφικής ομοιοθεσίας που πηγαίνει το  στο
στο  (αφού είναι η τομή των κύκλων
(αφού είναι η τομή των κύκλων 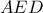 ,
,  ! (αποδεικνύεται εύκολα γωνιακά// δείτε άσκηση ΒΜΟ 2009).
! (αποδεικνύεται εύκολα γωνιακά// δείτε άσκηση ΒΜΟ 2009). . Εστω τώρα
. Εστω τώρα  τα μέσα των
τα μέσα των  . Αυτό σημαίνει ότι
. Αυτό σημαίνει ότι  ομοκυκλικά κι αφού ο κύκλος
ομοκυκλικά κι αφού ο κύκλος  περνάει απ' το
περνάει απ' το  έχουμε το ζητούμενο!
έχουμε το ζητούμενο!  Εύκολα αποδεικνύεται (εξ άλλου είναι το θεώρημα του
Εύκολα αποδεικνύεται (εξ άλλου είναι το θεώρημα του  από το οποίο διέρχονται οι περιγραμμένοι κύκλοι στα τρίγωνα ATD ,ABC,BTS, DCS. Άμεσα έχουμε
από το οποίο διέρχονται οι περιγραμμένοι κύκλοι στα τρίγωνα ATD ,ABC,BTS, DCS. Άμεσα έχουμε 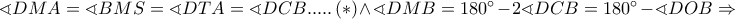

 .
.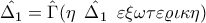 .
. . Από τις προηγούμενες σχέσεις προκύπτει
. Από τις προηγούμενες σχέσεις προκύπτει  και έτσι συμπεραίνουμε ότι
και έτσι συμπεραίνουμε ότι 
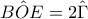 (Επίκεντρη-εγγεγραμμένη στον κύκλο (Ο)). Επίσης
(Επίκεντρη-εγγεγραμμένη στον κύκλο (Ο)). Επίσης 
 οπότε το ΒΜΕΟ είναι εγγράψιμο.
οπότε το ΒΜΕΟ είναι εγγράψιμο. οπότε
οπότε 

 , ότι
, ότι  είναι η πολική του
είναι η πολική του  κι άρα
κι άρα  . Ομοια προκύπτει (και αυτό που λες) ότι Κ ορθόκεντρο του
. Ομοια προκύπτει (και αυτό που λες) ότι Κ ορθόκεντρο του 
 επί την
επί την  είναι η πολική ευθεία του
είναι η πολική ευθεία του  ως προς τον περίκυκλο
ως προς τον περίκυκλο  του τετραπλεύρου
του τετραπλεύρου  και ως γνωστό, περνάει από το σημείο
και ως γνωστό, περνάει από το σημείο 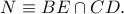
 ( σημείο τομής των διαγωνίων του
( σημείο τομής των διαγωνίων του 
 Όπως γράφει και ο Σωτήρης πιο πάνω, το
Όπως γράφει και ο Σωτήρης πιο πάνω, το  και λόγω του εγγραψίμου
και λόγω του εγγραψίμου 

