 εφάπτεται των πλευρών
εφάπτεται των πλευρών  στα σημεία
στα σημεία 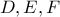 αντίστοιχα. Συμβολίζουμε με
αντίστοιχα. Συμβολίζουμε με τους περιγεγραμμένους κύκλους των τριγώνων
τους περιγεγραμμένους κύκλους των τριγώνων  αντίστοιχα.
αντίστοιχα.Οι κύκλοι
 τέμνονται στα σημεία
τέμνονται στα σημεία  και
και  , οι κύκλοι
, οι κύκλοι  στα
στα 
και οι κύκλοι
 στα
στα 
 Να δείξετε ότι οι κύκλοι
Να δείξετε ότι οι κύκλοι  τέμνονται σε ένα κοίνο σημείο.
τέμνονται σε ένα κοίνο σημείο. Να δείξετε ότι οι ευθείες
Να δείξετε ότι οι ευθείες  συντρέχουν.
συντρέχουν.Φιλικά,
Νίκος

 .
. απεκονίζεται στο
απεκονίζεται στο  .
. απεκονίζονται στις ευθείες
απεκονίζονται στις ευθείες  , τα σημεία
, τα σημεία  στα μέσα των
στα μέσα των  στο κύκλο Euler του
στο κύκλο Euler του  .
.  προβολή του
προβολή του  στην
στην  ,αντίστοιχα για τα
,αντίστοιχα για τα  . Αρκεί να δείξω ότι οι περιγεγραμμένοι κύκλοι των
. Αρκεί να δείξω ότι οι περιγεγραμμένοι κύκλοι των  ,
, ,
,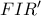 συντρέχουν σε σημείο διάφορο του
συντρέχουν σε σημείο διάφορο του  ορθόκεντρο του
ορθόκεντρο του  ...)
...) αντίστοιχα και
αντίστοιχα και  είναι το περίκεντρο. Τότε οι κύκλοι οι περιγεγραμμένοι των τριγώνων
είναι το περίκεντρο. Τότε οι κύκλοι οι περιγεγραμμένοι των τριγώνων 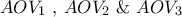 συντρέχουν σε σημείο (
συντρέχουν σε σημείο ( οι κύκλοι
οι κύκλοι  συντρέχουν στο έκκεντρο
συντρέχουν στο έκκεντρο  , τότε οι κύκλοι
, τότε οι κύκλοι  αντίστοιχα διότι διέρχονται απ τον πόλο
αντίστοιχα διότι διέρχονται απ τον πόλο  μένουν αμετάβλητα.
μένουν αμετάβλητα.  αντιστρέφονται στα
αντιστρέφονται στα  που είναι μέσα των
που είναι μέσα των  αντιστρέφονται στα
αντιστρέφονται στα  . Ο κύκλος
. Ο κύκλος  αντιστρέφεται σε κύκλο που διέρχεται από τα μέσα
αντιστρέφεται σε κύκλο που διέρχεται από τα μέσα  και επειδή αυτός διέρχεται κι από τα
και επειδή αυτός διέρχεται κι από τα  αντιστρέφονται στους περιγεγραμμένους κύκλους των τριγώνων
αντιστρέφονται στους περιγεγραμμένους κύκλους των τριγώνων  .
. εγγράψιμο. Πράγματι, ισχύει
εγγράψιμο. Πράγματι, ισχύει 
 έχουμε
έχουμε 
 ,που είναι προφανές.
,που είναι προφανές. .
.
 και
και  του τετραπλεύρου
του τετραπλεύρου  μεταφέρονται στις απέναντι γωνίες του εγγεγραμμένου
μεταφέρονται στις απέναντι γωνίες του εγγεγραμμένου  και έτσι είναι παραπληρωματικές.
και έτσι είναι παραπληρωματικές.