Καταπληκτικό θέμα 
 Λήμμα 1
Λήμμα 1

- ΔΓ1.jpg (37.42 KiB) Προβλήθηκε 2188 φορές
Τετράπλευρο

είναι εγγεγραμμένο σε κύκλο

. Οι πλευρές

τέμνονται στο σημείο

, οι πλευρές

τέμνονται στο σημείο

και οι διαγώνιοι

τέμνονται στο σημείο

. Τότε το

είναι ορθόκεντρο του τριγώνου

.
Το λήμμα αυτό κρύβει πολύ μεγάλο πλούτο υφής και το θεωρώ μεγάλης σπουδαιότητας. Υποθέτω πως θα είναι κάποιο θεώρημα. Δεν το βρήκα όμως κάπου (δεν διεκδικώ βέβαια σκορ διερεύνησης). Το αποδεικνύω στο τέλος, επί του παρόντος θα χρησιμοποιηθεί.
Λήμμα 2
Σε τετράπλευρο

, εγγεγραμμένο σε κύκλο

, οι διαγώνιοι τέμνονται στο σημείο

, οι πλευρές

στο σημείο

, οι πλευρές

στο σημείο

και έστω

τα μέσα των πλευρών

. Αν η

τέμνει την

στο σημείο

, τότε

.

- ΔΓ2.jpg (39.2 KiB) Προβλήθηκε 2188 φορές
Απόδειξη.
Από λήμμα 1 έχουμε ότι το σημείο

είναι ορθόκεντρο του τριγώνου

. Αν

το σημείο τομής των

τότε

. Επίσης

, επομένως τα σημεία

είναι ομοκυκλικά σε κύκλο διαμέτρου

(λόγω των ορθών γωνιών).
Οπότε θα έχουμε
 Στο θέμα μας.
Στο θέμα μας.

- ΔΓ3.jpg (28.43 KiB) Προβλήθηκε 2188 φορές
Αρκεί να αποδείξουμε ότι

. Τότε προκύπτει ότι η
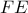
είναι εφαπτομένη του περιγεγραμμένου κύκλου του τριγώνου

(λόγω γωνίας χορδής και εφαπτομένης, ίσης με την αντίστοιχη εγγεγραμμένη).
Από λήμμα 2 έχουμε ότι

, τότε

, επομένως τα τρίγωνα

είναι όμοια (

).
Τότε

Τα τρίγωνα

είναι όμοια (προφανώς) και οι

είναι διάμεσοί τους, άρα τα τρίγωνα

είναι όμοια, οπότε

Αφαιρώντας τις

προκύπτει ότι

και η απόδειξη ολοκληρώθηκε.
Απόδειξη του αρχικόύ λήμματος
Λήμμα 1
Τετράπλευρο

είναι εγγεγραμμένο σε κύκλο

. Οι πλευρές

τέμνονται στο σημείο

, οι πλευρές

τέμνονται στο σημείο

και οι διαγώνιοι

τέμνονται στο σημείο

. Τότε το

είναι ορθόκεντρο του τριγώνου

.

- ΔΓ4.jpg (51.78 KiB) Προβλήθηκε 2188 φορές
Απόδειξη.
Φέρουμε τους περιγεγραμμένους κύκλους

των τριγώνων

οι οποίοι τέμνονται (εκτός του σημείου

) έστω στο σημείο

. Η

είναι ριζικός άξονας των

, η

είναι ριζικός άξονας των

και η

των

, άρα συντρέχουν, επομένως η

διέρχεται από το σημείο

.
Τα τετράπλευρα

είναι εγγράψιμμα (από κατασκευή). «Παίζοντας» με τις γωνίες τους έχουμε:

εγγράψιμο,

εγγράψιμο,

διχοτόμος της

,

εγγράψιμο,

διχοτόμος της

,

εγγράψιμο.
Δηλαδή βρέθηκε ότι τα

είναι εγγράψιμμα.
Επίσης

ριζικός άξονας των κύκλων των περιγεγραμμένων των τετραπλεύρων

,

ριζικός άξονας των κύκλων

και του περιγεγραμμένου στο τετράπλευρο

και

ριζικός άξονας των κύκλων

και του περιγεγραμμένου στο τετράπλευρο

, άρα συντρέχουν, επομένως η
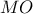
διέρχεται από το

.
Έστω

, η

διχοτόμος της

. Τότε

. Επομένως

.
Όμοια βρίσκουμε ότι

, επομένως το σημείο

είναι ορθόκεντρο του τριγώνου

.
Εξακολουθώ να πιστεύω πως το λήμμα 1 είναι κάποιο (άγνωστο σε μένα) θεώρημα.
 εγγράψιμο τετράπλευρο,όχι τραπέζιο και έστω
εγγράψιμο τετράπλευρο,όχι τραπέζιο και έστω  το σημείο τομής των διαγωνίων
το σημείο τομής των διαγωνίων  και
και  .Οι ευθείες
.Οι ευθείες 
 τέμνονται στο
τέμνονται στο  . Tα μέσα των
. Tα μέσα των  και
και  είναι τα σημεία
είναι τα σημεία  και
και  αντίστοιχα.
αντίστοιχα. εφάπτεται στο
εφάπτεται στο  του περιγεγραμμένου κύκλου του τριγώνου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου του τριγώνου  .
.
 είναι εγγεγραμμένο σε κύκλο
είναι εγγεγραμμένο σε κύκλο  . Οι πλευρές
. Οι πλευρές  τέμνονται στο σημείο
τέμνονται στο σημείο  τέμνονται στο σημείο
τέμνονται στο σημείο  και οι διαγώνιοι
και οι διαγώνιοι  τέμνονται στο σημείο
τέμνονται στο σημείο  .
. , οι διαγώνιοι τέμνονται στο σημείο
, οι διαγώνιοι τέμνονται στο σημείο  στο σημείο
στο σημείο  στο σημείο
στο σημείο  τα μέσα των πλευρών
τα μέσα των πλευρών  τέμνει την
τέμνει την  στο σημείο
στο σημείο  , τότε
, τότε  .
. . Αν
. Αν  το σημείο τομής των
το σημείο τομής των  τότε
τότε  . Επίσης
. Επίσης  , επομένως τα σημεία
, επομένως τα σημεία  είναι ομοκυκλικά σε κύκλο διαμέτρου
είναι ομοκυκλικά σε κύκλο διαμέτρου  (λόγω των ορθών γωνιών).
(λόγω των ορθών γωνιών).
 . Τότε προκύπτει ότι η
. Τότε προκύπτει ότι η 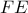 είναι εφαπτομένη του περιγεγραμμένου κύκλου του τριγώνου
είναι εφαπτομένη του περιγεγραμμένου κύκλου του τριγώνου  (λόγω γωνίας χορδής και εφαπτομένης, ίσης με την αντίστοιχη εγγεγραμμένη).
(λόγω γωνίας χορδής και εφαπτομένης, ίσης με την αντίστοιχη εγγεγραμμένη). , τότε
, τότε  , επομένως τα τρίγωνα
, επομένως τα τρίγωνα  είναι όμοια (
είναι όμοια ( ).
). 
 είναι όμοια (προφανώς) και οι
είναι όμοια (προφανώς) και οι  είναι διάμεσοί τους, άρα τα τρίγωνα
είναι διάμεσοί τους, άρα τα τρίγωνα  είναι όμοια, οπότε
είναι όμοια, οπότε 
 προκύπτει ότι
προκύπτει ότι  , οι πλευρές
, οι πλευρές  .
. των τριγώνων
των τριγώνων  οι οποίοι τέμνονται (εκτός του σημείου
οι οποίοι τέμνονται (εκτός του σημείου  . Η
. Η  είναι ριζικός άξονας των
είναι ριζικός άξονας των  και η
και η  , άρα συντρέχουν, επομένως η
, άρα συντρέχουν, επομένως η  είναι εγγράψιμμα (από κατασκευή). «Παίζοντας» με τις γωνίες τους έχουμε:
είναι εγγράψιμμα (από κατασκευή). «Παίζοντας» με τις γωνίες τους έχουμε:  εγγράψιμο,
εγγράψιμο,  εγγράψιμο,
εγγράψιμο,  διχοτόμος της
διχοτόμος της  ,
,  εγγράψιμο,
εγγράψιμο,  διχοτόμος της
διχοτόμος της  ,
,  εγγράψιμο.
εγγράψιμο. είναι εγγράψιμμα.
είναι εγγράψιμμα. ριζικός άξονας των κύκλων των περιγεγραμμένων των τετραπλεύρων
ριζικός άξονας των κύκλων των περιγεγραμμένων των τετραπλεύρων  ,
,  ριζικός άξονας των κύκλων
ριζικός άξονας των κύκλων  και του περιγεγραμμένου στο τετράπλευρο
και του περιγεγραμμένου στο τετράπλευρο  και
και  ριζικός άξονας των κύκλων
ριζικός άξονας των κύκλων  , άρα συντρέχουν, επομένως η
, άρα συντρέχουν, επομένως η 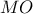 διέρχεται από το
διέρχεται από το  , η
, η  διχοτόμος της
διχοτόμος της  . Επομένως
. Επομένως  .
.  , επομένως το σημείο
, επομένως το σημείο  που τέμνονται ακόμα στο
που τέμνονται ακόμα στο  .
. .
.  ) ότι τα σημεία
) ότι τα σημεία  είναι αρμονικά συζυγή των
είναι αρμονικά συζυγή των  .
.  διέρχεται από το
διέρχεται από το  .
.  , αλλά
, αλλά  και άρα
και άρα  οπότε το
οπότε το  .
.