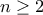 . Να δειχθεί ότι αν
. Να δειχθεί ότι αν  είναι φυσικοί αριθμοί τέτοιοι ώστε
είναι φυσικοί αριθμοί τέτοιοι ώστε  ,
, τότε ισχύει
 .
.Φιλικά,
Αχιλλέας
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
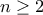 . Να δειχθεί ότι αν
. Να δειχθεί ότι αν  είναι φυσικοί αριθμοί τέτοιοι ώστε
είναι φυσικοί αριθμοί τέτοιοι ώστε  ,
,  .
.![\sum_{j=1}^{n}{x_{j}}\geq n\sqrt[n]{x_{1}x_{2}...x_{n}}\Leftrightarrow x_{1}x_{2}...x_{n}\geq n\left( x_{1}x_{2}...x_{n}\right)^{\frac{1}{n}}\Leftrightarrow \left(x_{1}x_{2}...x_{n} \right)^{\frac{n-1}{n}}\geq n\Leftrightarrow \left( x_{1}x_{2}...x_{n}\right)^{\frac{1}{n}}\geq n^{\frac{1}{n-1}}. \sum_{j=1}^{n}{x_{j}}\geq n\sqrt[n]{x_{1}x_{2}...x_{n}}\Leftrightarrow x_{1}x_{2}...x_{n}\geq n\left( x_{1}x_{2}...x_{n}\right)^{\frac{1}{n}}\Leftrightarrow \left(x_{1}x_{2}...x_{n} \right)^{\frac{n-1}{n}}\geq n\Leftrightarrow \left( x_{1}x_{2}...x_{n}\right)^{\frac{1}{n}}\geq n^{\frac{1}{n-1}}.](/forum/ext/geomar/texintegr/latexrender/pictures/efc76fd54d582676f96ed857eb0b2ff4.png)

Το 1ο σωστο, το 2ο λαθος. Πρωτου ποσταρεις μια λυση, σκεψου πρωτα μηπως αυτα που γραφεις δεν εχουν νοημα.kwstas12345 έγραψε:Για το κάτω φράγμα:
Eίναι:
Άρα:
Το άνω φράγμα:
 , και μετα για να δειξεις το αλλο αντιστρεφεις την ανισοτητα και εφαρμοζεις την
, και μετα για να δειξεις το αλλο αντιστρεφεις την ανισοτητα και εφαρμοζεις την  , οποτε στην ουσια κανεις οτι ακριβως εκανες και στο κατω φραγμα για να δειξεις το ανω, πραγμα που δεν εχει νοημα, και φτανεις εσφαλμενα στο ζητουμενο ανω φραγμα αγνοοντας το οτι η
, οποτε στην ουσια κανεις οτι ακριβως εκανες και στο κατω φραγμα για να δειξεις το ανω, πραγμα που δεν εχει νοημα, και φτανεις εσφαλμενα στο ζητουμενο ανω φραγμα αγνοοντας το οτι η  θα ειναι προφανως φθινουσα!!!
θα ειναι προφανως φθινουσα!!! , οποτε
, οποτε  για οποιαδηποτε επιλογη των n μεταβλητων (οχι απαραιτητα φυσικων, διοτι δεν χρησημοποιεις πουθενα οτι οι αριθμοι ειναι φυσικοι) που ικανοποιουν την συνθηκη!!!
για οποιαδηποτε επιλογη των n μεταβλητων (οχι απαραιτητα φυσικων, διοτι δεν χρησημοποιεις πουθενα οτι οι αριθμοι ειναι φυσικοι) που ικανοποιουν την συνθηκη!!! με την ισότητα να μην ισχύει αφού
με την ισότητα να μην ισχύει αφού  .
.Όχι, μόνο.kwstas12345 έγραψε:Μία λύση που σκέφτηκα (δεν ξέρω αν είναι σωστή):
H ισότητα ισχύει όταν όλοι οι αριθμοί ισούνται με 2.
Aπό την ανισότητα των δυνάμεων:
Όμοια:
Aρκεί ν.δ.ο:
που ισχύει...
 -άδα
-άδα  .
. ,
,  και
και  , τότε
, τότε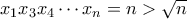 , έτσι δεν είναι;
, έτσι δεν είναι;Το να παρεις διακρινουσα σε τριωνυμο που ο συντελεστης του x ειναι 0 δεν εχει νοημα, και αυτα που γραφεις παραπανω δεν ισχυουν διοτι για να ειναι ενα αθροισμα θετικο δεν ειναι αναγκη και οι δυο προσθετετοι να ειναι θετικοι, και η διακρινουσα που παιρνεις δεν ειναι αναγκη να ειναι αρνητικη διοτι ενα τριωνυμο με θετικο συντελεστη μπορει να εχει θετικη διακρινουσα και να ειναι θετικο αν ο x βρησκεται παντα εξω απο το διαστημα που οριζουν οι ριζες.......kwstas12345 έγραψε:
Let's do it !! Λοιπόν ας υποθέσουμε λόγω συμμετρίας ότιachilleas έγραψε:Πάντως έχουν γραφτεί πολλά, κι ακόμα δεν έχει αποδειχθεί σχεδόν τίποτα...
 .
. από αυτούς είναι >1 , έστω οι
από αυτούς είναι >1 , έστω οι  Επομένως η συνθήκη γράφεται
Επομένως η συνθήκη γράφεται  και μας μένει να αποδείξουμε ότι
και μας μένει να αποδείξουμε ότι  . Θέτουμε
. Θέτουμε  κτλ. Τότε
κτλ. Τότε  και μας μένει νδο
και μας μένει νδο 
 παίρνουμε το ζητούμενο για
παίρνουμε το ζητούμενο για 

Πολύ σωστά! Αυτή είναι η ιδέα!smar έγραψε:Let's do it !! Λοιπόν ας υποθέσουμε λόγω συμμετρίας ότιachilleas έγραψε:Πάντως έχουν γραφτεί πολλά, κι ακόμα δεν έχει αποδειχθεί σχεδόν τίποτα....
Προφανώς δε γίνεται n-1 από αυτούς να είναι μονάδες. Υποθέτουμε ότιαπό αυτούς είναι >1 , έστω οι
Επομένως η συνθήκη γράφεται
και μας μένει να αποδείξουμε ότι
. Θέτουμε
κτλ. Τότε
η συνθήκη γράφεταικαι μας μένει νδο
Ανοίγοντας το δεξί μέλος και χρησιμοποιώντας ότιπαίρνουμε το ζητούμενο για
(νομίζω!! δεν είμαι πολύ σίγουρος για τις πράξεις, αλλά αυτό είναι το γενικό concept!)
Αν τώρα k=2 νομίζω ότι είναι πολύ εύκολο.
Όπου από εκεί θα μας βγει και η ισότητα έχω την εντύπωση δηλαδή η ν-άδα
 άρτιος και
άρτιος και  φυσικοί αριθμοί οι οποίοι ικανοποιούν την σχέση
φυσικοί αριθμοί οι οποίοι ικανοποιούν την σχέση  ,
,  διαιρείται με 4.
διαιρείται με 4. Αν όλοι ήταν περιττοί τότε το δεξί μέλος είναι περιττός ενώ το αριστερό άρτιος (αφού είναι άθροισμα άρτιου πλήθους περιττών προσθετέων), άτοπο.nkatsipis έγραψε: Την λύση του προβλήματος την είχα διαβάσει παλαιότερα σε ένα όμορφο άρθρο το οποίο θα ανεβάσω αφού απαντηθεί και το παρακάτω (πιο εύκολο) ερώτημα
Ανάρτιος και
φυσικοί αριθμοί οι οποίοι ικανοποιούν την σχέση
,
δείξτε ότι ο αριθμόςδιαιρείται με 4.
Φιλικά,
Νίκος Κατσίπης
 διαιρείται από το
διαιρείται από το  συνεπώς και το
συνεπώς και το  διαιρείται από το
διαιρείται από το  .
.Κομψό !! Λοιπόν αν όλοι οι αριθμοί ήταν περιττοί τότε το πρώτο μέλος θα ήταν άρτιος, ενώ το δεύτερο περιττός. Αν τώρα υπάρχει ακριβώς ένας άρτιος τότε το πρώτο μέλος είναι περιττός και το δεύτερο άρτιος. Άρα υπάρχουν δύο άρτιοι και πάνω άραnkatsipis έγραψε: Ανάρτιος και
φυσικοί αριθμοί οι οποίοι ικανοποιούν την σχέση
,
δείξτε ότι ο αριθμόςδιαιρείται με 4.
 . Νομίζω ότι παρόμοια αποτελέσματα μπορούμε να βρούμε και όταν
. Νομίζω ότι παρόμοια αποτελέσματα μπορούμε να βρούμε και όταν 
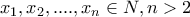 ,
,  , και
, και  το πληθος των
το πληθος των  με,
με,  . Νδο
. Νδο 
Η παραπάνω άσκηση του Νίκου έχει ξεχαστεί οπότε την επαναφέρω.Nick1990 έγραψε:Επισης ενω προσπαθουσα να βρω λυση στο αρχικο, βρηκα ενα αλλο πιο χαλαρο αποτελεσμα (αν φυσικα δεν εχω χασει κατι στις πραξεις):
Αν,
, και
το πληθος των
με,
. Νδο
άλλη μία επαναφορά μετά από 8 και πλέον χρόνια!achilleas έγραψε: ↑Κυρ Ιούλ 18, 2010 8:25 pmΗ παραπάνω άσκηση του Νίκου έχει ξεχαστεί οπότε την επαναφέρω.Nick1990 έγραψε:Επισης ενω προσπαθουσα να βρω λυση στο αρχικο, βρηκα ενα αλλο πιο χαλαρο αποτελεσμα (αν φυσικα δεν εχω χασει κατι στις πραξεις):
Αν,
, και
το πληθος των
με,
. Νδο
Φιλικά,
Αχιλλέας
 το οποίο (για
το οποίο (για  ) είναι καλύτερο φράγμα.
) είναι καλύτερο φράγμα. και έστω επίσης ότι
και έστω επίσης ότι  για
για  . Τότε
. Τότε 
 υπάρχουν
υπάρχουν  όροι, όλοι μεγαλύτεροι ή ίσου του
όροι, όλοι μεγαλύτεροι ή ίσου του  . Κρατήσαμε τους
. Κρατήσαμε τους  και για τους άλλους τους βάλαμε ίσους με
και για τους άλλους τους βάλαμε ίσους με  .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης