 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
β) Να προσδιορίσετε όλες τις συναρτήσεις
 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Έστω
 , για κάθε
, για κάθε  . Τότε, η δοσμένη σχέση γράφεται
. Τότε, η δοσμένη σχέση γράφεται
 δεν είναι η μηδενική. Αρχίζουμε με κάποιους Ισχυρισμούς:
δεν είναι η μηδενική. Αρχίζουμε με κάποιους Ισχυρισμούς: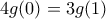 .
. και
και  διαδοχικά στην αρχική έχουμε
διαδοχικά στην αρχική έχουμε

 και
και  . Τώρα, έχουμε ότι
. Τώρα, έχουμε ότι


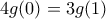 , όπως θέλαμε
, όπως θέλαμε 

 .
. .
.



 , για κάθε
, για κάθε  .
. και
και  δίνει το ζητούμενο, χρησιμοποιώντας τον Ισχυρισμό 2
δίνει το ζητούμενο, χρησιμοποιώντας τον Ισχυρισμό 2 
 .
.


 , προκύπτει
, προκύπτει 

 , για κάθε
, για κάθε  .
. είναι προφανές. Αν ισχύει για κάποιο
είναι προφανές. Αν ισχύει για κάποιο  , τότε με
, τότε με  στο αποτέλεσμα του Ισχυρισμού 3 και χρησιμοποιώντας το Πόρισμα του Ισχυρισμού 2 προκύπτει
στο αποτέλεσμα του Ισχυρισμού 3 και χρησιμοποιώντας το Πόρισμα του Ισχυρισμού 2 προκύπτει

 , και άρα έχουμε τον επόμενο Ισχυρισμό:
, και άρα έχουμε τον επόμενο Ισχυρισμό: , για κάθε
, για κάθε  .
.

 και
και  η αρχική δίνει
η αρχική δίνει
 και
και  δίνει
δίνει

 . Είναι
. Είναι 



 .
. , και άρα η αρχική με
, και άρα η αρχική με  και
και  διαδοχικά δίνει,
διαδοχικά δίνει,
 για κάθε
για κάθε  , άτοπο αφού υποθέσαμε ότι η
, άτοπο αφού υποθέσαμε ότι η  δεν είναι η μηδενική.
δεν είναι η μηδενική. , και άρα
, και άρα  , συνάρτηση η οποία προφανώς επαληθεύει.
, συνάρτηση η οποία προφανώς επαληθεύει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες