 για τις οποίες ισχύει
για τις οποίες ισχύει  για κάθε
για κάθε 
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
 για τις οποίες ισχύει
για τις οποίες ισχύει  για κάθε
για κάθε 
 (1)
(1) :
: 
 και
και  :
: 
 :
:  (2)
(2) :
:  (3)
(3)

 επαληθεύει την (1) οπότε είναι δεκτή ως λύση.
επαληθεύει την (1) οπότε είναι δεκτή ως λύση. δεν είναι η μηδενική τότε θα έχουμε
δεν είναι η μηδενική τότε θα έχουμε  ή
ή  ή
ή 
 τότε το
τότε το 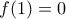 οπότε η
οπότε η  και
και  δίνει :
δίνει : 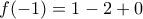 οπότε
οπότε 
 και
και  :
:  Άτοπο
Άτοπο τότε το
τότε το  και
και 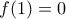 οπότε η
οπότε η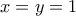 :
:  Άτοπο
Άτοπο
 δεν είναι η μηδενική.
δεν είναι η μηδενική.  για το οποίο
για το οποίο 
 :
:  Από την παραπάνω σχέση εύκολα αποδεικνύεται ότι η
Από την παραπάνω σχέση εύκολα αποδεικνύεται ότι η  είναι
είναι  στο
στο 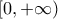 καθώς και στο
καθώς και στο ![(-\infty,0] (-\infty,0]](/forum/ext/geomar/texintegr/latexrender/pictures/15a0f0419a82bd06453c59063f91aad0.png) .
. :
:  (4)
(4) :
: 

 και καθώς τα
και καθώς τα  και
και  ανήκουν στο
ανήκουν στο 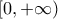
 .
.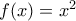 που επαληθεύει,
που επαληθεύει, που επίσης επαληθεύει καθώς και όλες οι κλαδικές που φτιάχνονται από αυτούς τους τύπους και αλλάζουν σε κάποιο πραγματικό
που επίσης επαληθεύει καθώς και όλες οι κλαδικές που φτιάχνονται από αυτούς τους τύπους και αλλάζουν σε κάποιο πραγματικό  .
.Δύσκολη!simantiris j. έγραψε: ↑Κυρ Μαρ 29, 2015 2:26 pmΝα βρείτε όλες τις συναρτήσειςγια τις οποίες ισχύει
για κάθε

 δεν είναι η μηδενική.
δεν είναι η μηδενική. για κάποια
για κάποια  τότε
τότε  ή
ή  .
. για το οποίο
για το οποίο  , τότε η αρχική με
, τότε η αρχική με  και
και  και
και  διαδοχικά δίνει ότι
διαδοχικά δίνει ότι
 , συνεπώς αφού
, συνεπώς αφού  έχουμε το ζητούμενο
έχουμε το ζητούμενο 

 δίνει
δίνει  , και με
, και με  δίνει
δίνει  .
. και παίρνοντας
και παίρνοντας  και
και  διαδοχικά στην αρχική προκύπτει ότι
διαδοχικά στην αρχική προκύπτει ότι

 , είναι
, είναι

 . Τότε, είναι
. Τότε, είναι  . Με
. Με  και
και  η αρχική δίνει
η αρχική δίνει
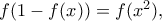

 .
. και
και  .
. και
και  (πράγματι, αν
(πράγματι, αν  τότε
τότε  , άρα
, άρα  , άτοπο).
, άτοπο). είναι πεπερασμένο.
είναι πεπερασμένο. είναι μη κενό. Μπορούμε να υποθέσουμε ότι
είναι μη κενό. Μπορούμε να υποθέσουμε ότι  . Έστω
. Έστω  . Τότε, με
. Τότε, με  στην αρχική έχουμε ότι
στην αρχική έχουμε ότι
 τέτοια, ώστε
τέτοια, ώστε
 , οπότε προκύπτει
, οπότε προκύπτει  , άρα
, άρα  , οπότε
, οπότε  ή
ή  . Όμως, η αρχική με
. Όμως, η αρχική με  και
και  δίνει
δίνει  , οπότε έχουμε άτοπο.
, οπότε έχουμε άτοπο. , οπότε προκύπτει
, οπότε προκύπτει  , άτοπο.
, άτοπο. , οπότε προκύπτει
, οπότε προκύπτει  , άτοπο αφού
, άτοπο αφού  .
. , οπότε προκύπτει
, οπότε προκύπτει  , άτοπο αφού
, άτοπο αφού  .
.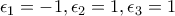 , οπότε προκύπτει
, οπότε προκύπτει  , δηλαδή
, δηλαδή  .
. , οπότε προκύπτει
, οπότε προκύπτει  , άρα
, άρα  , άτοπο.
, άτοπο. , οπότε προκύπτει
, οπότε προκύπτει  , άτοπο.
, άτοπο. , οπότε προκύπτει
, οπότε προκύπτει  , άρα
, άρα  , που δίνει
, που δίνει  , άρα
, άρα  .
. τότε το τυχόν
τότε το τυχόν  μπορεί να πάρει το πολύ
μπορεί να πάρει το πολύ  διαφορετικές τιμές, οπότε έχουμε ότι
διαφορετικές τιμές, οπότε έχουμε ότι  , άρα το
, άρα το  είναι πεπερασμένο
είναι πεπερασμένο 
 είναι πεπερασμένο, ο επόμενος στόχος είναι να δείξουμε ότι
είναι πεπερασμένο, ο επόμενος στόχος είναι να δείξουμε ότι  . Έστω προς άτοπο ότι
. Έστω προς άτοπο ότι  , και έστω
, και έστω  . Αφού το
. Αφού το  είναι πεπερασμένο και
είναι πεπερασμένο και  , το
, το  είναι άπειρο. Έστω ένα
είναι άπειρο. Έστω ένα  , το οποίο θα επιλέξουμε κατάλληλα αργότερα.
, το οποίο θα επιλέξουμε κατάλληλα αργότερα. και
και  δίνει ότι
δίνει ότι
 ώστε
ώστε

 , άτοπο για κατάλληλη επιλογή του
, άτοπο για κατάλληλη επιλογή του  .
. , και άρα
, και άρα  για κάθε
για κάθε  , η οποία και επαληθεύει.
, η οποία και επαληθεύει. . Χειριζόμαστε ανάλογα αυτήν την περίπτωση, οπότε και προκύπτει η λύση
. Χειριζόμαστε ανάλογα αυτήν την περίπτωση, οπότε και προκύπτει η λύση 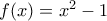 .
. . Τότε, με
. Τότε, με  η αρχική δίνει
η αρχική δίνει  , και άρα από τον Ισχυρισμό 1 είναι
, και άρα από τον Ισχυρισμό 1 είναι  , για κάθε
, για κάθε  .
. και
και  .
. είναι κενό, τότε προκύπτουν οι λύσεις
είναι κενό, τότε προκύπτουν οι λύσεις  και
και  . Ας υποθέσουμε τώρα ότι
. Ας υποθέσουμε τώρα ότι  . Σαφώς ισχύει
. Σαφώς ισχύει  και
και  .
. , τότε
, τότε  .
. , και ένα
, και ένα  . Τότε η αρχική με
. Τότε η αρχική με  και
και  δίνει
δίνει
 τέτοια, ώστε
τέτοια, ώστε 
 είναι άμεσο να δούμε ότι πρέπει
είναι άμεσο να δούμε ότι πρέπει  , και άρα
, και άρα  , δηλαδή
, δηλαδή  , όπως θέλαμε. Επίσης προκύπτει ότι
, όπως θέλαμε. Επίσης προκύπτει ότι  .
. 
 είναι το κενό.
είναι το κενό.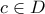 , τότε με
, τότε με  η αρχική δίνει
η αρχική δίνει

 , άτοπο αφού
, άτοπο αφού  .
. είναι πράγματι το κενό
είναι πράγματι το κενό 
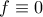 ,
,  ,
,  ,
, 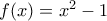 και
και  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες