 θετικών ακεραίων που είναι τέτοιοι ώστε:
θετικών ακεραίων που είναι τέτοιοι ώστε: 
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
 θετικών ακεραίων που είναι τέτοιοι ώστε:
θετικών ακεραίων που είναι τέτοιοι ώστε: 
Καλησπέρα σε όλους! Μία προσπάθεια:smar έγραψε:Να βρεθούν όλα τα ζεύγηθετικών ακεραίων που είναι τέτοιοι ώστε:
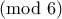 προκύπτει
προκύπτει  άρτιος. Γράφω
άρτιος. Γράφω  και θέτω
και θέτω  . Τότε η εξίσωση γίνεται:
. Τότε η εξίσωση γίνεται: .
. .
.
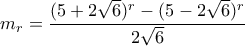
 γίνεται δύναμη του
γίνεται δύναμη του  .
. άρτιος. Τότε από το διωνυμικό θέωρημα προκύπτει:
άρτιος. Τότε από το διωνυμικό θέωρημα προκύπτει:
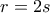 τότε
τότε 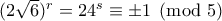 και άρα το αριστερό μέλος είναι πολλαπλάσιο του
και άρα το αριστερό μέλος είναι πολλαπλάσιο του  ενώ το δεξί όχι, άτοπο.
ενώ το δεξί όχι, άτοπο. περιττός. Πάλι από το διωνυμικό θεώρημα προκύπτει:
περιττός. Πάλι από το διωνυμικό θεώρημα προκύπτει:
 τότε όμοια με την προηγούμενη περίπτωση προκύπτει άτοπο. Άρα πρέπει
τότε όμοια με την προηγούμενη περίπτωση προκύπτει άτοπο. Άρα πρέπει  .
. που είναι και μοναδική.
που είναι και μοναδική.
 οπότε
οπότε  άρα
άρα  άρτιος και έστω
άρτιος και έστω  ,
, 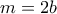 ,
,  θετικός ακέραιος.
θετικός ακέραιος. και επειδή
και επειδή  ,
,  ,
, , και
, και  δεν διαιρεί τον
δεν διαιρεί τον  επομένως
επομένως  άρα
άρα  --(τα 2 κλάσματα είναι ακέραιοι και πρώτοι μεταξύ τους ) συνεπώς υπάρχει
--(τα 2 κλάσματα είναι ακέραιοι και πρώτοι μεταξύ τους ) συνεπώς υπάρχει  θετικός ακέραιος ώστε
θετικός ακέραιος ώστε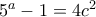 ,
,  συνεπώς από mihailescu θα έχει μοναδική λύση την
συνεπώς από mihailescu θα έχει μοναδική λύση την  οπότε μοναδική λύση το ζεύγος
οπότε μοναδική λύση το ζεύγος
 για
για  έχει μοναδική λύση την
έχει μοναδική λύση την 

 τότε
τότε  άρα
άρα  για θετικό
για θετικό  αλλά με
αλλά με  αντίφαση.
αντίφαση.Ψάχνοντας για Pell έπεσα πάνω σε αυτή, νομίζω πως η παραπάνω λύση έχει πρόβλημα στην περίπτωση πουraf616 έγραψε: ↑Σάβ Μαρ 28, 2015 6:56 pmΚαλησπέρα σε όλους! Μία προσπάθεια:smar έγραψε:Να βρεθούν όλα τα ζεύγηθετικών ακεραίων που είναι τέτοιοι ώστε:
Μεπροκύπτει
άρτιος. Γράφω
και θέτω
. Τότε η εξίσωση γίνεται:
.
Πρόκειται για εξίσωση Pell με θεμελιώδη λύση.
Γνωρίζουμε ότι οι λύσεις δίνονται από τους τύπους:
Θα δούμε πότε ογίνεται δύναμη του
.
Έστω αρχικάάρτιος. Τότε από το διωνυμικό θέωρημα προκύπτει:
Αντότε
και άρα το αριστερό μέλος είναι πολλαπλάσιο του
ενώ το δεξί όχι, άτοπο.
Έστω τώραπεριττός. Πάλι από το διωνυμικό θεώρημα προκύπτει:
Αντότε όμοια με την προηγούμενη περίπτωση προκύπτει άτοπο. Άρα πρέπει
.
Εύκολα τώρα προκύπτει η λύσηπου είναι και μοναδική.
 περιττός.
περιττός.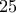 το οποίο δεν ισχύει π.χ για
το οποίο δεν ισχύει π.χ για  και αυτό γιατί κρύβεται ένα
και αυτό γιατί κρύβεται ένα  στον
στον  .
. θέτουμε
θέτουμε  και
και  και για ευκολία
και για ευκολία  οπότε έχουμε την Pell
οπότε έχουμε την Pell  με
με  η θεμελιώδης λύση.
η θεμελιώδης λύση. και
και 
 άρα
άρα 
 :
: 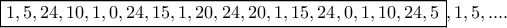 και μετά επαναλαμβάνεται.
και μετά επαναλαμβάνεται. (όχι τυχαίο, είναι
(όχι τυχαίο, είναι 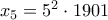 ) :
) : και μετά επαναλαμβάνεται.
και μετά επαναλαμβάνεται.
 να είναι δύναμη του
να είναι δύναμη του  θα πρέπει
θα πρέπει  και έτσι προκύπτει η μοναδική λύση
και έτσι προκύπτει η μοναδική λύση 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης