 -γώνου. Ονομάζουμε μια από αυτές τις διαγωνίους καλή αν τέμνει (εσωτερικά του πολυγώνου) ακριβώς μία άλλη από τις διαγωνίους που σχεδιάσαμε. Να βρεθεί ο μέγιστος δυνατός αριθμός καλών διαγωνίων.
-γώνου. Ονομάζουμε μια από αυτές τις διαγωνίους καλή αν τέμνει (εσωτερικά του πολυγώνου) ακριβώς μία άλλη από τις διαγωνίους που σχεδιάσαμε. Να βρεθεί ο μέγιστος δυνατός αριθμός καλών διαγωνίων.Τεμνόμενες διαγώνιοι
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Τεμνόμενες διαγώνιοι
Φέρουμε ορισμένες από τις διαγωνίους ενός κυρτού  -γώνου. Ονομάζουμε μια από αυτές τις διαγωνίους καλή αν τέμνει (εσωτερικά του πολυγώνου) ακριβώς μία άλλη από τις διαγωνίους που σχεδιάσαμε. Να βρεθεί ο μέγιστος δυνατός αριθμός καλών διαγωνίων.
-γώνου. Ονομάζουμε μια από αυτές τις διαγωνίους καλή αν τέμνει (εσωτερικά του πολυγώνου) ακριβώς μία άλλη από τις διαγωνίους που σχεδιάσαμε. Να βρεθεί ο μέγιστος δυνατός αριθμός καλών διαγωνίων.
 -γώνου. Ονομάζουμε μια από αυτές τις διαγωνίους καλή αν τέμνει (εσωτερικά του πολυγώνου) ακριβώς μία άλλη από τις διαγωνίους που σχεδιάσαμε. Να βρεθεί ο μέγιστος δυνατός αριθμός καλών διαγωνίων.
-γώνου. Ονομάζουμε μια από αυτές τις διαγωνίους καλή αν τέμνει (εσωτερικά του πολυγώνου) ακριβώς μία άλλη από τις διαγωνίους που σχεδιάσαμε. Να βρεθεί ο μέγιστος δυνατός αριθμός καλών διαγωνίων.Re: Τεμνόμενες διαγώνιοι
Διαγραφή. Είχα διαβάσει λάθος την εκφώνηση. Ευχαριστώ τον κύριο Δημήτρη για την επισήμανση και ζητώ συγγνώμη απ'όσους ταλαιπώρησα.
Μιχάλης Σαράντης
Re: Τεμνόμενες διαγώνιοι
Έστω 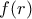 ο μέγιστος αριθμός καλών διαγωνίων σε ένα κυρτό r-γωνο
ο μέγιστος αριθμός καλών διαγωνίων σε ένα κυρτό r-γωνο  . Εύκολα
. Εύκολα  . θα δείξω με ισχυρη επαγωγή ότι
. θα δείξω με ισχυρη επαγωγή ότι
 . Έστω ισχύει για κάθε
. Έστω ισχύει για κάθε  . θα δείξω ότι ισχύει και για
. θα δείξω ότι ισχύει και για  .
.
Έστω το κυρτό πολύγωνο, τότε φέρνοντας τις διαγωνίους:
το κυρτό πολύγωνο, τότε φέρνοντας τις διαγωνίους:  ,
,  ,
,
 εύκολα βλέπουμε ότι είναι όλες καλές άρα
εύκολα βλέπουμε ότι είναι όλες καλές άρα  .
.
Έστω ότι υπήρχε σχηματισμός με παραπάνω απο καλές διαγωνίους τότε πρφανώς υπάρχουν 2 καλές διαγώνιοι που τέμνονται μέσα στο πολύγωνο, έστω
καλές διαγωνίους τότε πρφανώς υπάρχουν 2 καλές διαγώνιοι που τέμνονται μέσα στο πολύγωνο, έστω  . Τότε αυτές οι δύο το χωρίζουν σε 4 περιοχές σημείων, τις
. Τότε αυτές οι δύο το χωρίζουν σε 4 περιοχές σημείων, τις  (περιλαμβάνοντας και τα ακριανά σημεία). Αφού οι
(περιλαμβάνοντας και τα ακριανά σημεία). Αφού οι  καλές δεν υπάρχουν διαγώνιοι από μία περιοχή σε άλλη.
καλές δεν υπάρχουν διαγώνιοι από μία περιοχή σε άλλη.
Έστω λοιπόν ότι οι περιοχές έχουν σημεία, τότε προφανώς
σημεία, τότε προφανώς  και προφανώς ο μέγιστος αριθμός καλών διαγωνίων είναι
και προφανώς ο μέγιστος αριθμός καλών διαγωνίων είναι  . Για
. Για  απο επαγωγική υπόθεση
απο επαγωγική υπόθεση  , άρα
, άρα
 , άτοπο. Άρα
, άτοπο. Άρα  , οπότε
, οπότε  .
.
Έστω το κυρτό πολύγωνο, τότε φέρνοντας τις διαγωνίους:
το κυρτό πολύγωνο, τότε φέρνοντας τις διαγωνίους:  και
και  βλέπουμε ότι υπάρχουν 2K-2 καλές διαγώνιοι, οπότε
βλέπουμε ότι υπάρχουν 2K-2 καλές διαγώνιοι, οπότε  . Έστω ότι υπήρχε σχηματισμός με τουλάχιστον
. Έστω ότι υπήρχε σχηματισμός με τουλάχιστον  καλές διαγωνίους , τότε πάλι υπάρχουν 2 που τέμνονται στο πολύγωνο, έστω
καλές διαγωνίους , τότε πάλι υπάρχουν 2 που τέμνονται στο πολύγωνο, έστω  . Τότε αυτές οι δύο το χωρίζουν ξανά σε 4 περιοχές σημείων, τις
. Τότε αυτές οι δύο το χωρίζουν ξανά σε 4 περιοχές σημείων, τις  με
με
 σημεία αντοίστιχα οπότε
σημεία αντοίστιχα οπότε  . τουλάχιστον ένας από τους
. τουλάχιστον ένας από τους  είναι περιττος, έστω ο
είναι περιττος, έστω ο  , τότε
, τότε
(αφου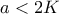 )
)  . Τότε έχουμε
. Τότε έχουμε  , άτοπο. Άρα
, άτοπο. Άρα
 , οπότε
, οπότε  .
.
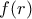 ο μέγιστος αριθμός καλών διαγωνίων σε ένα κυρτό r-γωνο
ο μέγιστος αριθμός καλών διαγωνίων σε ένα κυρτό r-γωνο  . Εύκολα
. Εύκολα  . θα δείξω με ισχυρη επαγωγή ότι
. θα δείξω με ισχυρη επαγωγή ότι  . Έστω ισχύει για κάθε
. Έστω ισχύει για κάθε  . θα δείξω ότι ισχύει και για
. θα δείξω ότι ισχύει και για  .
.Έστω
 το κυρτό πολύγωνο, τότε φέρνοντας τις διαγωνίους:
το κυρτό πολύγωνο, τότε φέρνοντας τις διαγωνίους:  ,
,  ,
, εύκολα βλέπουμε ότι είναι όλες καλές άρα
εύκολα βλέπουμε ότι είναι όλες καλές άρα  .
. Έστω ότι υπήρχε σχηματισμός με παραπάνω απο
 καλές διαγωνίους τότε πρφανώς υπάρχουν 2 καλές διαγώνιοι που τέμνονται μέσα στο πολύγωνο, έστω
καλές διαγωνίους τότε πρφανώς υπάρχουν 2 καλές διαγώνιοι που τέμνονται μέσα στο πολύγωνο, έστω  . Τότε αυτές οι δύο το χωρίζουν σε 4 περιοχές σημείων, τις
. Τότε αυτές οι δύο το χωρίζουν σε 4 περιοχές σημείων, τις  (περιλαμβάνοντας και τα ακριανά σημεία). Αφού οι
(περιλαμβάνοντας και τα ακριανά σημεία). Αφού οι  καλές δεν υπάρχουν διαγώνιοι από μία περιοχή σε άλλη.
καλές δεν υπάρχουν διαγώνιοι από μία περιοχή σε άλλη.Έστω λοιπόν ότι οι περιοχές έχουν
 σημεία, τότε προφανώς
σημεία, τότε προφανώς  και προφανώς ο μέγιστος αριθμός καλών διαγωνίων είναι
και προφανώς ο μέγιστος αριθμός καλών διαγωνίων είναι  . Για
. Για  απο επαγωγική υπόθεση
απο επαγωγική υπόθεση  , άρα
, άρα , άτοπο. Άρα
, άτοπο. Άρα  , οπότε
, οπότε  .
.Έστω
 το κυρτό πολύγωνο, τότε φέρνοντας τις διαγωνίους:
το κυρτό πολύγωνο, τότε φέρνοντας τις διαγωνίους:  και
και  βλέπουμε ότι υπάρχουν 2K-2 καλές διαγώνιοι, οπότε
βλέπουμε ότι υπάρχουν 2K-2 καλές διαγώνιοι, οπότε  . Έστω ότι υπήρχε σχηματισμός με τουλάχιστον
. Έστω ότι υπήρχε σχηματισμός με τουλάχιστον  καλές διαγωνίους , τότε πάλι υπάρχουν 2 που τέμνονται στο πολύγωνο, έστω
καλές διαγωνίους , τότε πάλι υπάρχουν 2 που τέμνονται στο πολύγωνο, έστω  . Τότε αυτές οι δύο το χωρίζουν ξανά σε 4 περιοχές σημείων, τις
. Τότε αυτές οι δύο το χωρίζουν ξανά σε 4 περιοχές σημείων, τις  με
με  σημεία αντοίστιχα οπότε
σημεία αντοίστιχα οπότε  . τουλάχιστον ένας από τους
. τουλάχιστον ένας από τους  είναι περιττος, έστω ο
είναι περιττος, έστω ο  , τότε
, τότε(αφου
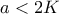 )
)  . Τότε έχουμε
. Τότε έχουμε  , άτοπο. Άρα
, άτοπο. Άρα , οπότε
, οπότε  .
.Πέτρος Ντούνης
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Τεμνόμενες διαγώνιοι
Πέτρο πολύ καλά. Η λύση σου είναι κάπως πιο απλή από την δική μου. Είχα προσπαθήσει το ίδιο αλλά νόμιζα πως δεν θα δούλευε και έτσι κατέληξα σε μια λίγο διαφορετική λύση:
Ονομάζω μια από τις διαγωνίους που φέραμε εξαιρετική αν τέμνει το πολύ μία άλλη διαγώνιο. Έστω ο μέγιστος αριθμός των εξαιρετικών διαγωνίων. Θα δείξω ότι
ο μέγιστος αριθμός των εξαιρετικών διαγωνίων. Θα δείξω ότι  αν
αν  άρτιος και
άρτιος και  αν
αν  περιττός.
περιττός.
Αν δεν υπάρχουν καλές διαγώνιοι τότε όντως υπάρχουν το πολύ εξαιρετικές. Έστω λοιπόν μια καλή διαγώνιος. Χωρίς βλάβη ενώνει τα
εξαιρετικές. Έστω λοιπόν μια καλή διαγώνιος. Χωρίς βλάβη ενώνει τα  και
και  . Οπότε χωρίζει το πολύγωνο στα πολύγωνα
. Οπότε χωρίζει το πολύγωνο στα πολύγωνα  και
και  . Γνωρίζουμε ότι υπάρχει ακριβώς μία διαγώνιος
. Γνωρίζουμε ότι υπάρχει ακριβώς μία διαγώνιος 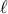 μεταξύ των δυο κομματιών. Αγνοώντας την, από την επαγωγική υπόθεση έχουμε το πολύ
μεταξύ των δυο κομματιών. Αγνοώντας την, από την επαγωγική υπόθεση έχουμε το πολύ  εξαιρετικές διαγωνίους στο πρώτο πολύγωνο και
εξαιρετικές διαγωνίους στο πρώτο πολύγωνο και  εξαιρετικές διαγωνίους στο δεύτερο πολύγωνο. Προσθέτωντας την
εξαιρετικές διαγωνίους στο δεύτερο πολύγωνο. Προσθέτωντας την 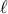 ίσως καταστρέψουμε κάποιες από αυτές τις εξαιρετικές διαγωνίους αλλά δεν δημιουργούμε καινούργιες εκτός ίσως από την ίδια την
ίσως καταστρέψουμε κάποιες από αυτές τις εξαιρετικές διαγωνίους αλλά δεν δημιουργούμε καινούργιες εκτός ίσως από την ίδια την 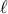 . [Αυτός είναι και ο λόγος που χρειάστηκε τις εξαιρετικές διαγωνίους.] Οπότε έχουμε το πολύ
. [Αυτός είναι και ο λόγος που χρειάστηκε τις εξαιρετικές διαγωνίους.] Οπότε έχουμε το πολύ  εξαιρετικές διαγωνίους. Για
εξαιρετικές διαγωνίους. Για  άρτιο από την επαγωγική υπόθεση είναι
άρτιο από την επαγωγική υπόθεση είναι  . Για
. Για  περιττό τουλάχιστον ένα από τα
περιττό τουλάχιστον ένα από τα  είναι περιττό οπότε από την επαγωγική υπόθεση είναι
είναι περιττό οπότε από την επαγωγική υπόθεση είναι  .
.
Πέτρο συμφωνώ με την κρίση σου. Ίσως δεν είναι τόσο δύσκολο για medium πιστεύω όμως ότι είναι άνετα ένα easy πρόβλημα ΙΜΟ. Το πρόβλημα το πήρα από τον φετινό ρωσικό διαγωνισμό για grade 9, το οποίο νομίζω αντιστοιχεί σε Α' Λυκείου. (Δείτε εδώ. Η πρώτη λύση είναι ίδια με αυτήν του Πέτρου.) Για grade 9 το θεωρώ πως είναι πολύ δύσκολο (ιδίως αφού δεν δίνεται η τελική απάντηση) και ήθελα να σιγουρευτώ μήπως μου διαφεύγει κάτι απλό.
Ονομάζω μια από τις διαγωνίους που φέραμε εξαιρετική αν τέμνει το πολύ μία άλλη διαγώνιο. Έστω
 ο μέγιστος αριθμός των εξαιρετικών διαγωνίων. Θα δείξω ότι
ο μέγιστος αριθμός των εξαιρετικών διαγωνίων. Θα δείξω ότι  αν
αν  άρτιος και
άρτιος και  αν
αν  περιττός.
περιττός. Αν δεν υπάρχουν καλές διαγώνιοι τότε όντως υπάρχουν το πολύ
 εξαιρετικές. Έστω λοιπόν μια καλή διαγώνιος. Χωρίς βλάβη ενώνει τα
εξαιρετικές. Έστω λοιπόν μια καλή διαγώνιος. Χωρίς βλάβη ενώνει τα  και
και  . Οπότε χωρίζει το πολύγωνο στα πολύγωνα
. Οπότε χωρίζει το πολύγωνο στα πολύγωνα  και
και  . Γνωρίζουμε ότι υπάρχει ακριβώς μία διαγώνιος
. Γνωρίζουμε ότι υπάρχει ακριβώς μία διαγώνιος 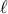 μεταξύ των δυο κομματιών. Αγνοώντας την, από την επαγωγική υπόθεση έχουμε το πολύ
μεταξύ των δυο κομματιών. Αγνοώντας την, από την επαγωγική υπόθεση έχουμε το πολύ  εξαιρετικές διαγωνίους στο πρώτο πολύγωνο και
εξαιρετικές διαγωνίους στο πρώτο πολύγωνο και  εξαιρετικές διαγωνίους στο δεύτερο πολύγωνο. Προσθέτωντας την
εξαιρετικές διαγωνίους στο δεύτερο πολύγωνο. Προσθέτωντας την 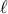 ίσως καταστρέψουμε κάποιες από αυτές τις εξαιρετικές διαγωνίους αλλά δεν δημιουργούμε καινούργιες εκτός ίσως από την ίδια την
ίσως καταστρέψουμε κάποιες από αυτές τις εξαιρετικές διαγωνίους αλλά δεν δημιουργούμε καινούργιες εκτός ίσως από την ίδια την 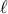 . [Αυτός είναι και ο λόγος που χρειάστηκε τις εξαιρετικές διαγωνίους.] Οπότε έχουμε το πολύ
. [Αυτός είναι και ο λόγος που χρειάστηκε τις εξαιρετικές διαγωνίους.] Οπότε έχουμε το πολύ  εξαιρετικές διαγωνίους. Για
εξαιρετικές διαγωνίους. Για  άρτιο από την επαγωγική υπόθεση είναι
άρτιο από την επαγωγική υπόθεση είναι  . Για
. Για  περιττό τουλάχιστον ένα από τα
περιττό τουλάχιστον ένα από τα  είναι περιττό οπότε από την επαγωγική υπόθεση είναι
είναι περιττό οπότε από την επαγωγική υπόθεση είναι  .
.Πέτρο συμφωνώ με την κρίση σου. Ίσως δεν είναι τόσο δύσκολο για medium πιστεύω όμως ότι είναι άνετα ένα easy πρόβλημα ΙΜΟ. Το πρόβλημα το πήρα από τον φετινό ρωσικό διαγωνισμό για grade 9, το οποίο νομίζω αντιστοιχεί σε Α' Λυκείου. (Δείτε εδώ. Η πρώτη λύση είναι ίδια με αυτήν του Πέτρου.) Για grade 9 το θεωρώ πως είναι πολύ δύσκολο (ιδίως αφού δεν δίνεται η τελική απάντηση) και ήθελα να σιγουρευτώ μήπως μου διαφεύγει κάτι απλό.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες
