 με πλευρές
με πλευρές  ημιπερίμετρο
ημιπερίμετρο  για το οποίο ισχύει
για το οποίο ισχύει . (
. ( )
) Να αποδείξετε ότι το βαρύκεντρο
Να αποδείξετε ότι το βαρύκεντρο 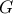 του τριγώνου είναι σημείο του εγγεγραμμένου κύκλου.
του τριγώνου είναι σημείο του εγγεγραμμένου κύκλου. Να βρείτε τα τρίγωνα που ικανοποιούν την (
Να βρείτε τα τρίγωνα που ικανοποιούν την ( ) και έχουν πλευρές με ακέραια μήκη.
) και έχουν πλευρές με ακέραια μήκη.***Ευχαριστώ τον Σωτήρη Λουρίδα για την επισήμανση αβλεψίας.

 :
:


![\displaystyle{ \Leftrightarrow {b^2} + {c^2} + 9{a^2} = 4\left[ {{a^2} - {{\left( {b - c} \right)}^2}} \right] \Leftrightarrow {b^2} + {c^2} + 9{a^2} = 4{a^2} - 4{b^2} - 4{c^2} + 8bc \Leftrightarrow } \displaystyle{ \Leftrightarrow {b^2} + {c^2} + 9{a^2} = 4\left[ {{a^2} - {{\left( {b - c} \right)}^2}} \right] \Leftrightarrow {b^2} + {c^2} + 9{a^2} = 4{a^2} - 4{b^2} - 4{c^2} + 8bc \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/1268deb188a449bf51fc404645959920.png)

 .
. είναι το έγκεντρο του τριγώνου
είναι το έγκεντρο του τριγώνου 
 .
.
 .
.  η ακτίνα του εγγεγραμμένου κύκλου στο τρίγωνο
η ακτίνα του εγγεγραμμένου κύκλου στο τρίγωνο ![\displaystyle{I{A^2} + I{B^2} + I{C^2} = \frac{1}{4}\left[ {{{\left( {b + c - a} \right)}^2} + {{\left( {c + a - b} \right)}^2} + {{\left( {a + b - c} \right)}^2}} \right] + 3{r^2} \Leftrightarrow } \displaystyle{I{A^2} + I{B^2} + I{C^2} = \frac{1}{4}\left[ {{{\left( {b + c - a} \right)}^2} + {{\left( {c + a - b} \right)}^2} + {{\left( {a + b - c} \right)}^2}} \right] + 3{r^2} \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/10766694b6a99557158d17eaa0067027.png)

 .
. 

 .
. , δηλαδή με το σημείο
, δηλαδή με το σημείο