 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Γιαsocrates έγραψε:Να προσδιορίσετε όλες τις συναρτήσειςτέτοιες ώστε
(1)για κάθε
 η (1) δίνει
η (1) δίνει 
 , τότε η (1) για
, τότε η (1) για  δίνει
δίνει  , δεκτή, γιατί επαληθεύει την αρχική.
, δεκτή, γιατί επαληθεύει την αρχική. , τότε η (1) για
, τότε η (1) για  δίνει
δίνει 
 , αλλά και
, αλλά και 

 (2)
(2) δίνει
δίνει  , άρα
, άρα  (3)
(3) , τότε
, τότε  , κατά συνέπεια
, κατά συνέπεια ,
, , τότε
, τότε , κατά συνέπεια
, κατά συνέπεια ,
, τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Αρχικά παρατηρούμε ότι αν η
 ικανοποιεί την συνθήκη τότε και η
ικανοποιεί την συνθήκη τότε και η  την ικανοποιεί, οπότε χωρίς βλάβη της γενικότητας υποθέτουμε ότι
την ικανοποιεί, οπότε χωρίς βλάβη της γενικότητας υποθέτουμε ότι  .
. η δοσμένη δίνει
η δοσμένη δίνει  , συνεπώς εύκολα επαγωγικά
, συνεπώς εύκολα επαγωγικά  για κάθε
για κάθε  . Παίρνοντας λοιπόν τα
. Παίρνοντας λοιπόν τα  θετικούς ακεραίους στην δοσμένη, προκύπτει ότι
θετικούς ακεραίους στην δοσμένη, προκύπτει ότι
 (υποθέσαμε ότι
(υποθέσαμε ότι  ).
). για κάποιο
για κάποιο  , τότε
, τότε  για κάθε
για κάθε  .
. η δοσμένη με
η δοσμένη με  και
και  δίνει
δίνει
 , μπορούμε να γράψουμε
, μπορούμε να γράψουμε  για κάθε
για κάθε  .
.  .
.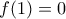 . Τότε,
. Τότε,  , δηλαδή
, δηλαδή  , για κάθε
, για κάθε  . Αποδεικνύουμε επαγωγικά το εξής:
. Αποδεικνύουμε επαγωγικά το εξής: και για κάθε
και για κάθε  ισχύει ότι
ισχύει ότι  .
.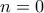 είναι άμεσο. Αν ισχύει για κάποιο
είναι άμεσο. Αν ισχύει για κάποιο  , τότε έστω ένα τυχόν
, τότε έστω ένα τυχόν  . Αν
. Αν  τότε προφανώς
τότε προφανώς  , οπότε ας υποθέσουμε ότι
, οπότε ας υποθέσουμε ότι  .
. η δοσμένη δίνει
η δοσμένη δίνει 

 . Άρα,
. Άρα,
 ή
ή  .
. με
με  ήταν
ήταν  , τότε αφού
, τότε αφού  , ο Ισχυρισμός 1 δίνει ότι
, ο Ισχυρισμός 1 δίνει ότι  . Συνεπώς, σε κάθε περίπτωση είναι
. Συνεπώς, σε κάθε περίπτωση είναι  , οπότε ο Ισχυρισμός αποδείχθηκε
, οπότε ο Ισχυρισμός αποδείχθηκε 
 . Τότε, για
. Τότε, για  είναι από την ανισότητα Bernoulli,
είναι από την ανισότητα Bernoulli,
 , άρα από τον Ισχυρισμό 2 προκύπτει ότι
, άρα από τον Ισχυρισμό 2 προκύπτει ότι  . Συνεπώς,
. Συνεπώς,  για όλα τα
για όλα τα  , δηλαδή η
, δηλαδή η  είναι ταυτοτικά μηδέν, συνάρτηση η οποία προφανώς επαληθεύει.
είναι ταυτοτικά μηδέν, συνάρτηση η οποία προφανώς επαληθεύει. . Τότε, είναι
. Τότε, είναι  , για κάθε
, για κάθε  άρα άμεσα επαγωγικά προκύπτει ότι
άρα άμεσα επαγωγικά προκύπτει ότι
 και
και  . Από εδώ φαίνεται ότι
. Από εδώ φαίνεται ότι  , για κάθε
, για κάθε  .
. , για κάθε
, για κάθε  .
. τέτοιο, ώστε
τέτοιο, ώστε  . Τότε, αφού
. Τότε, αφού  , ισχύει ότι
, ισχύει ότι
 , συνεπώς με διαδοχικές εφαρμογές αυτής προκύπτει ότι
, συνεπώς με διαδοχικές εφαρμογές αυτής προκύπτει ότι  . Τότε, όμως, είναι
. Τότε, όμως, είναι  , άρα από τον Ισχυρισμό 1 προκύπτει ότι
, άρα από τον Ισχυρισμό 1 προκύπτει ότι 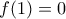 , το οποίο είναι άτοπο
, το οποίο είναι άτοπο 
 στην δοσμένη, όπου
στην δοσμένη, όπου  τυχαίος θετικός ακέραιος, είναι
τυχαίος θετικός ακέραιος, είναι

 .
. στην δοσμένη, όπου
στην δοσμένη, όπου  τυχαίος θετικός ακέραιος, είναι
τυχαίος θετικός ακέραιος, είναι

 .
. η πιο πάνω δίνει
η πιο πάνω δίνει  , άρα έχουμε ότι
, άρα έχουμε ότι
 για κάθε
για κάθε  , οπότε από τον Ισχυρισμό 3 είναι
, οπότε από τον Ισχυρισμό 3 είναι  για κάθε
για κάθε  .
.
 , συνεπώς
, συνεπώς  για κάθε
για κάθε  . Τώρα, έστω ένα
. Τώρα, έστω ένα  και
και  τέτοιο, ώστε
τέτοιο, ώστε
 και αφού
και αφού και
και 
 , οπότε από την αρχική σχέση άμεσα προκύπτει ότι
, οπότε από την αρχική σχέση άμεσα προκύπτει ότι  . Συνεπώς,
. Συνεπώς,  για κάθε
για κάθε  , και σαφώς και αυτή η συνάρτηση ικανοποιεί.
, και σαφώς και αυτή η συνάρτηση ικανοποιεί.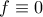 και
και  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες