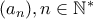 , ώστε να ισχύει:
, ώστε να ισχύει: για κάθε
για κάθε  φυσικό, όχι μηδέν.
φυσικό, όχι μηδέν.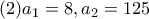
Να βρείτε σε πόσα μηδενικά λήγει ο αριθμός

Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
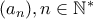 , ώστε να ισχύει:
, ώστε να ισχύει: για κάθε
για κάθε  φυσικό, όχι μηδέν.
φυσικό, όχι μηδέν.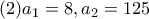

Η αναδρομική σχέση γράφεταιchris_gatos έγραψε:Έστω η ακολουθία τωv φυσικών αριθμών, ώστε να ισχύει:
για κάθε
φυσικό, όχι μηδέν.
Να βρείτε σε πόσα μηδενικά λήγει ο αριθμός
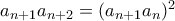 .
. οπότε
οπότε  και επαγωγικά
και επαγωγικά 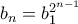 . Άρα
. Άρα  .
. οπότε θέτοντας
οπότε θέτοντας 
 οπότε
οπότε  .
. και
και 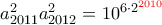 .
. και
και 

 τελειώνει σε
τελειώνει σε  μηδενικά.
μηδενικά.
 είναι το 2 και το 5 άρα
είναι το 2 και το 5 άρα 




 λήγει σε
λήγει σε  μηδενικά
μηδενικά τα μηδενικά και όχι
τα μηδενικά και όχι  ; Το λέω γιατι π.χ. στη δεύτερη απόδειξη,
; Το λέω γιατι π.χ. στη δεύτερη απόδειξη,  . Ή μήπως δεν βλέπω κάτι καλά (το πιο πιθανό γιατί και οι δυο λύσεις βγάζουν το ίδιο αποτέλεσμα).
. Ή μήπως δεν βλέπω κάτι καλά (το πιο πιθανό γιατί και οι δυο λύσεις βγάζουν το ίδιο αποτέλεσμα).
Χρήστο, Κώστα ευχαριστώ για την υπόδειξη του λάθους.chris_gatos έγραψε:Κώστα(Kostas_94) καλησπέρα.
O γενικός τύπος της λύσης που έχω είναι:
Νομίζω πως είναι δικαιολογημένη η αιτιασή σου, αλλά δε μπορώ να βρω και ψεγάδι στη λύση.
Κι εγώ χτες είχα πρόβλημα αλλά δεν έβγαζα άκρη με τις πράξεις.
Καλό απόγευμα.
chris_gatos έγραψε: ↑Τετ Μαρ 07, 2012 4:11 pmΈστω η ακολουθία τωv φυσικών αριθμών, ώστε να ισχύει:
για κάθε
φυσικό, όχι μηδέν.
Να βρείτε σε πόσα μηδενικά λήγει ο αριθμός
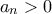 για κάθε
για κάθε 
 τότε
τότε  που είναι γραμμική, ομογενής αναδρομική ακολουθία με χαρακτηριστική εξίσωση
που είναι γραμμική, ομογενής αναδρομική ακολουθία με χαρακτηριστική εξίσωση 
 και
και  οπότε
οπότε 
 τα βρίσκουμε από τις αρχικές συνθήκες
τα βρίσκουμε από τις αρχικές συνθήκες 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης