 με
με  , να αποδειχθεί ότι :
, να αποδειχθεί ότι :
Μπάμπης
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan




 και διαδοχικά έχουμε
και διαδοχικά έχουμε  .Επειδή
.Επειδή 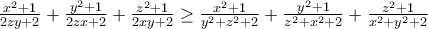 ,αρκεί
,αρκεί  .Θέτω
.Θέτω  και η ανισότητα γράφεται
και η ανισότητα γράφεται  .Η τελευταία ανισότητα είναι η ανισότητα Nesbitt και δίνω μια ενδεικτική απόδειξη της.
.Η τελευταία ανισότητα είναι η ανισότητα Nesbitt και δίνω μια ενδεικτική απόδειξη της.
Αντί να κάνεις μόνο δήλωση, καλό θα ήταν να βλέπαμε κιόλας την λύση σου. Αλλιώς είναι άνευ περιεχομένου, και μάλιστα για ερώτημα που τέθηκε πρινchristodoulos703 έγραψε:Αντί για BCS βγαίνει και με ανισότητα της αναδιάταξης και Andreescu.
 χρόνια.
χρόνια.Υπενθύμιση.Mihalis_Lambrou έγραψε:Αντί να κάνεις μόνο δήλωση, καλό θα ήταν να βλέπαμε κιόλας την λύση σου. Αλλιώς είναι άνευ περιεχομένου, και μάλιστα για ερώτημα που τέθηκε πρινchristodoulos703 έγραψε:Αντί για BCS βγαίνει και με ανισότητα της αναδιάταξης και Andreescu.χρόνια.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες