Μέγιστο ύψος

KARKAR · #1

: Μέγιστο ύψος.png (32.83 KiB) Προβλήθηκε 2501 φορές

Σημείο

κινείται σε ημικύκλιο διαμέτρου

. Με βάση την

και προς τα "πάνω" ,

σχεδιάζω το ισόπλευρο τρίγωνο PAS

. Βρείτε το μέγιστο ύψος της κορυφής

#2

KARKAR έγραψε:Μέγιστο ύψος.pngΣημείο κινείται σε ημικύκλιο διαμέτρου . Με βάση την και προς τα "πάνω" ,

σχεδιάζω το ισόπλευρο τρίγωνο . Βρείτε το μέγιστο ύψος της κορυφής

Ας πούμε πρώτα δυο λόγια για την κατασκευή που μεγιστοποιεί το ύψος

: Μέγιστο ύψος.png (12.27 KiB) Προβλήθηκε 2439 φορές

Έστω

το κέντρο και το μέσο του ημικυκλίου και

το μέσο του

. Από το

φέρνω παράλληλη στην

που τέμνει

το ημικύκλιο στα σημεία H, S

(το

πιο κοντά στο

). Η κατασκευή (προς τα πάνω) του ισοπλεύρου ASP

ορίζει την θέση του

.

#3

Στην άσκησή μας τώρα. Θα δείξω ότι $\displaystyle{\omega = \varphi = {15^0}}$

: Μέγιστο ύψος.2.png (10.04 KiB) Προβλήθηκε 2423 φορές

Έστω

η ακτίνα του ημικυκλίου και

η πλευρά του ισοπλεύρου. $\displaystyle{a = 2R\cos \omega ,h = a\cos \varphi \Rightarrow }$ $\boxed{h = 2R\cos \omega \cos \varphi }$

Αρκεί λοιπόν να βρούμε τη μέγιστη τιμή του γινομένου $\boxed{\cos \omega \cos \varphi }$ . Αλλά λόγω του ισοπλεύρου είναι φανερό ότι $\displaystyle{\omega + \varphi = {30^0}}$

$\displaystyle{\cos \omega \cos \varphi = \cos \omega \cos ({30^0} - \omega ) = \frac{{\sqrt 3 }}{2}{\cos ^2}\omega + \frac{1}{2}\sin \omega \cos \omega = \frac{{\sqrt 3 }}{4}(1 + \cos 2\omega ) + \frac{1}{4}\sin 2\omega = }$

$\displaystyle{\frac{{\sqrt 3 }}{4} + \frac{1}{2}\cos ({30^0} - 2\omega ) \le \frac{{\sqrt 3 + 2}}{4}}$ , για $\displaystyle{\omega = \varphi = {15^0}}$ . Άρα: $\boxed{{h_{\max }} = \frac{R}{2}\left( {\sqrt 3 + 2} \right)}$

ΥΓ. Και στα δύο σχήματα υπάρχει ένα σημείο

. Αγνοήστε το.

Al.Koutsouridis · #4

KARKAR έγραψε:Μέγιστο ύψος.pngΣημείο κινείται σε ημικύκλιο διαμέτρου . Με βάση την και προς τα "πάνω" ,

σχεδιάζω το ισόπλευρο τρίγωνο . Βρείτε το μέγιστο ύψος της κορυφής

Καλησπέρα,

: μέγιστο_ύψος.png (33.75 KiB) Προβλήθηκε 2389 φορές

Έστω

ισόπλευρο τρίγωνο με την κορυφή

προς την πλευρά του ημικυκλίου και ας είναι

το σημείο τομής των ευθειών PS, CB

. Τότε εφόσον $\angle APM = \angle ACM = 60^0$ , τα σημεία A,P,C,M

είναι ομοκυκλικά.

Επίσης έχουμε για τις γωνίες ASM

και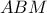

να είναι είτε ίσες είτε παραπληρωματικές (ανάλογα αν το

είναι εντός ή εκτός του τμήματος

). Οπότε

ομοκυκλικά άρα το

είναι σημείο του αρχικού ημικυκλίου και $AM \perp BC$ . Δηλαδή το

είναι το μέσο της

και είναι σταθερό.

Από τα παραπάνω παρατηρούμε ότι τα A,C, M

ορίζουν σταθερό κύκλο διαμέτρου

και επομένως το

κινείτε επί του ημικυκλίου

που δεν περιέχει το

.

Επομένως το μέγιστο ύψος θα επιτευχθεί όταν το

θα συμπέσει με το βόρειο πόλο του κύκλου. Στην περίπτωση αυτή το ύψος θα διέρχεται από το κέντρο του κύκλου, έστω

, και θα είναι ίσο με

συν το ύψος ισόπλευρου τριγώνου πλευράς

. Δηλαδή $R+\dfrac{\sqrt{3}}{2}R$ .

Μέγιστο ύψος

Μέγιστο ύψος

Re: Μέγιστο ύψος

Re: Μέγιστο ύψος

Re: Μέγιστο ύψος

Μέλη σε σύνδεση