Όμορφο θέμα, αν και δύσκολο, με σημαντική σκέψη που λύνεται και με στοιχειώδη εργαλεία.
Θα ήθελα να μου επιτραπεί να από-αγιοποιήσω για λίγο την μέθοδο της αντιστροφής, χωρίς βέβαια και προφανώς να υπάρχει η παραμικρή υπόνοια για προσπάθεια υποβάθμισης της Άριστης αυτής μεθόδου. Απλά προϋπάρχουν και πιο στοιχειώδεις μέθοδοι επίλυσης.
1. Για την «Κατασκευή πρώτη» δεν είναι υποχρεωτικό στο βάθος του μυαλού να υπάρχει η γνώση της αντιστροφής. Αρκεί να σκεφτεί κάποιος το προηγούμενο, τουλάχιστον χρονικά κατά την εξέλιξη των Μαθηματικών, σκεπτικό ότι το γινόμενο δύο ευθυγράμμων τμημάτων μπορεί να προκύψει από ομοιότητα τριγώνων για πλευρές που δεν βρίσκονται αντίστοιχα απέναντι από ίσες γωνίες, αρκεί από την αναλογία να κάνουμε το «χιαστί», όπως λαϊκά λέμε. Με βάση λοιπόν το σκεπτικό αυτό επέλυσα το θέμα κάτω από τον τίτλο «Κατασκευή πρώτη», αφού δημιούργησα τρίγωνο

, όμοιο στο τρίγωνο

και συνέχισα κανονικά (
https://mathematica.gr/forum/viewtopic. ... 94#p330694).
2. Για την κατασκευή κάτω από τον τίτλο (που όπως και η πρώτη γενικεύονται ως προς τα δεδομένα και πέραν των αριθμητικών που σωστά έβαλε ο Κώστας, ώστε να συγκεντρωθούν περισσότερο οι λύτες) «Κατασκευή δεύτερη» και μετά από την Άριστη λύση του Νίκου και μόνο για λόγους πλουραλισμού και διδακτικής προσέγγισης προτείνω και την διαπραγμάτευση που ακολουθεί.
ΑΝΑΛΥΣΗ (και με βάση το σχήμα της
ανάλυσης που προφανώς δεν έχει την ακρίβεια του σχήματος της κατασκευής αφού η ανάλυση, που είναι η καθοριστική και πλέον σπουδαία
προ απαιτούμενη διαδικασία, προσανατολίζει προς την απόλυτα ακριβή κατασκευή, για τούτο στην ανάλυση ξεκινάμε με την φράση: Έστω ότι υπάρχει .........):
Έστω λοιπόν

η τομή της ημιευθείας

με τον δεδομένο κύκλο

. Τότε παίρνουμε

Άρα προκύπτει

Αυτό οδηγεί στο συμπέρασμα ότι το ορθογώνιο τρίγωνο

παραμένει όμοιο προς εαυτόν, οπότε διατηρεί τις γωνίες του. Εδώ ακριβώς θεωρούμε ορθογώνιο τρίγωνο
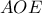
«ομορρόπως» όμοιο στο τρίγωνο

οπότε

Από την ομοιότητα αυτή προκύπτει άμεσα η «ομορρόπως» ομοιότητα των τριγώνων

με πλευρά

ομόλογη της πλευράς

,
και πλευρά

ομόλογη της πλευράς

και έτσι έχουμε:

Συνεπώς το σημείο

προσδιορίζεται ως τομή του κύκλου

και της ευθείας

. Άμεσα πλέον έχουμε την ζητούμενη κατασκευή.

- 2η κατ..png (21.3 KiB) Προβλήθηκε 930 φορές
edit: Απλά διόρθωσα σε

το

που εκ παραδρομής είχε γραφεί.
 και ευθεία
και ευθεία  η οποία απέχει από το κέντρο
η οποία απέχει από το κέντρο  απόσταση
απόσταση  .
. και το
και το  απόσταση
απόσταση  , όπως φαίνεται στο ακόλουθο σχήμα:
, όπως φαίνεται στο ακόλουθο σχήμα: , τέτοιο ώστε οι κορυφές
, τέτοιο ώστε οι κορυφές  να ανήκουν αντίστοιχα στον κύκλο
να ανήκουν αντίστοιχα στον κύκλο  και
και  κι ακόμα να είναι:
κι ακόμα να είναι: 

 και δύναμη αντιστροφής
και δύναμη αντιστροφής 
 (κόκκινος) που τον στρέφω γύρω από το
(κόκκινος) που τον στρέφω γύρω από το  (πράσινος ) που τέμνει
(πράσινος ) που τέμνει  που είναι και τα ζητούμενα .
που είναι και τα ζητούμενα . τέμνει τον αρχικό κύκλο στο
τέμνει τον αρχικό κύκλο στο  .
. προς το
προς το  τέτοιο ώστε :
τέτοιο ώστε :  που με ώθησε να κάνω την αντιστροφή του κύκλου.
που με ώθησε να κάνω την αντιστροφή του κύκλου. )
)  ένα άλλο γινόμενο .
ένα άλλο γινόμενο . , όμοιο στο τρίγωνο
, όμοιο στο τρίγωνο  και συνέχισα κανονικά (
και συνέχισα κανονικά ( η τομή της ημιευθείας
η τομή της ημιευθείας  . Τότε παίρνουμε
. Τότε παίρνουμε  Άρα προκύπτει
Άρα προκύπτει  Αυτό οδηγεί στο συμπέρασμα ότι το ορθογώνιο τρίγωνο
Αυτό οδηγεί στο συμπέρασμα ότι το ορθογώνιο τρίγωνο  παραμένει όμοιο προς εαυτόν, οπότε διατηρεί τις γωνίες του. Εδώ ακριβώς θεωρούμε ορθογώνιο τρίγωνο
παραμένει όμοιο προς εαυτόν, οπότε διατηρεί τις γωνίες του. Εδώ ακριβώς θεωρούμε ορθογώνιο τρίγωνο 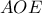 «ομορρόπως» όμοιο στο τρίγωνο
«ομορρόπως» όμοιο στο τρίγωνο  οπότε
οπότε 
 με πλευρά
με πλευρά  ομόλογη της πλευράς
ομόλογη της πλευράς  ,
,  και έτσι έχουμε:
και έτσι έχουμε: 
 προσδιορίζεται ως τομή του κύκλου
προσδιορίζεται ως τομή του κύκλου  και της ευθείας
και της ευθείας  . Άμεσα πλέον έχουμε την ζητούμενη κατασκευή.
. Άμεσα πλέον έχουμε την ζητούμενη κατασκευή.  το
το  που εκ παραδρομής είχε γραφεί.
που εκ παραδρομής είχε γραφεί.