Σελίδα 1 από 1
ΥΠΕΡΒΟΛΗ
Δημοσιεύτηκε: Παρ Ιουν 17, 2016 3:47 am
από Mαριάννα
Καλησπέρα σας !
Θα ήθελα να με βοηθήσετε στην παρακάτω άσκηση :
Πώς μπορώ να βρω τα άκρα της χορδής

της υπερβολής με εξίσωση

η οποία διχοτομείται από το σημείο

;
Σας ευχαριστώ πολύ !
Re: ΥΠΕΡΒΟΛΗ
Δημοσιεύτηκε: Παρ Ιουν 17, 2016 7:47 am
από Doloros
Mαριάννα έγραψε:Καλησπέρα σας !
Θα ήθελα να με βοηθήσετε στην παρακάτω άσκηση :
Πώς μπορώ να βρω τα άκρα της χορδής

της υπερβολής με εξίσωση

η οποία διχοτομείται από το σημείο

;
Σας ευχαριστώ πολύ !
Μια ιδέα (λίγο συμπυκνωμένα) .

- υπερβολή.png (14.94 KiB) Προβλήθηκε 1821 φορές
Η ευθεία μ’ εξίσωση
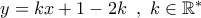
διέρχεται πάντα από το

ενώ η κατακόρυφη δια του

προφανώς δεν αποτελεί λύση του προβλήματος.
Το σύστημα

μας δίδει την εξίσωση :
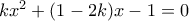
.
Από τους τύπους

έχουμε
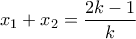
και πρέπει

και άρα

.
Μετά απ’ αυτά τα άκρα είναι

.
Re: ΥΠΕΡΒΟΛΗ
Δημοσιεύτηκε: Παρ Ιουν 17, 2016 4:28 pm
από Mαριάννα
σας ευχαριστώ πάρα πολύ !!!
Re: ΥΠΕΡΒΟΛΗ
Δημοσιεύτηκε: Σάβ Ιουν 18, 2016 12:01 am
από Soteris
Χρησιμοποιώντας το πιο πάνω σχήμα..
Έστω

με

.
Το σημείο

είναι το μέσον του ευθύγραμμου τμήματος

, συνεπώς:

Από το πιο πάνω σύστημα προκύπτει η εξίσωση

, με λύσεις τις
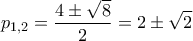
.
Τελικά, τα άκρα του ευθύγραμμου τμήματος

έχουν συντεταγμένες

.
Επεξεργασία: Αλλαγή στην ονομασία των σημείων

και

, λόγω επεξεργασίας του σχήματος από τον Doloros.
 της υπερβολής με εξίσωση
της υπερβολής με εξίσωση  η οποία διχοτομείται από το σημείο
η οποία διχοτομείται από το σημείο  ;
; της υπερβολής με εξίσωση
της υπερβολής με εξίσωση  η οποία διχοτομείται από το σημείο
η οποία διχοτομείται από το σημείο  ;
;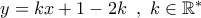 διέρχεται πάντα από το
διέρχεται πάντα από το  ενώ η κατακόρυφη δια του
ενώ η κατακόρυφη δια του  προφανώς δεν αποτελεί λύση του προβλήματος.
προφανώς δεν αποτελεί λύση του προβλήματος. μας δίδει την εξίσωση :
μας δίδει την εξίσωση : 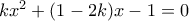 .
. έχουμε
έχουμε 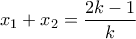 και πρέπει
και πρέπει  και άρα
και άρα  .
. .
. με
με  .
.  είναι το μέσον του ευθύγραμμου τμήματος
είναι το μέσον του ευθύγραμμου τμήματος  , συνεπώς:
, συνεπώς: 
 , με λύσεις τις
, με λύσεις τις 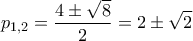 .
. .
. και
και  , λόγω επεξεργασίας του σχήματος από τον Doloros.
, λόγω επεξεργασίας του σχήματος από τον Doloros.