 , οι κύριες διευθύνσεις διχοτομούν τις ασυμπτωτικές διευθύνσεις.
, οι κύριες διευθύνσεις διχοτομούν τις ασυμπτωτικές διευθύνσεις.Υπερβολικό σημείο επιφάνειας
Συντονιστής: matha
- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Υπερβολικό σημείο επιφάνειας
Να αποδειχθεί ότι σε ένα υπερβολικό σημείο μιας κανονικής επιφάνειας στον  , οι κύριες διευθύνσεις διχοτομούν τις ασυμπτωτικές διευθύνσεις.
, οι κύριες διευθύνσεις διχοτομούν τις ασυμπτωτικές διευθύνσεις.
 , οι κύριες διευθύνσεις διχοτομούν τις ασυμπτωτικές διευθύνσεις.
, οι κύριες διευθύνσεις διχοτομούν τις ασυμπτωτικές διευθύνσεις.
-
trefoil_knot
- Δημοσιεύσεις: 3
- Εγγραφή: Σάβ Οκτ 24, 2015 9:12 am
Re: Υπερβολικό σημείο επιφάνειας
Αν  μοναδιαία διανύσματα προς τις δυό κύριες διευθύνσεις και
μοναδιαία διανύσματα προς τις δυό κύριες διευθύνσεις και  η γωνία που διαγράφει μια ασυμπτωτική διεύθυνση με μία κύρια διεύθυνση (wlog.
η γωνία που διαγράφει μια ασυμπτωτική διεύθυνση με μία κύρια διεύθυνση (wlog.  ) τότε από τον τύπο Euler για την κάθετη καμπυλότητα (αυτόν εδώ)
) τότε από τον τύπο Euler για την κάθετη καμπυλότητα (αυτόν εδώ) 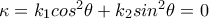 αφού βρισκόμαστε σε ασυμπτωτική διεύθυνση. Άρα
αφού βρισκόμαστε σε ασυμπτωτική διεύθυνση. Άρα  (το σημείο είναι υπερβολικό επομένως η Gaussian
(το σημείο είναι υπερβολικό επομένως η Gaussian  ) και
) και  , επομένως οι γωνίες
, επομένως οι γωνίες  βρίσκονται επίσης σε ασυμπτωτικές διευθύνσεις, δηλαδή οι ασυμπτωτικές διευθύνσεις διχοτομούνται από τις κύριες διευθύνσεις (όπως δείχνει το σύστημα αναφοράς μας
βρίσκονται επίσης σε ασυμπτωτικές διευθύνσεις, δηλαδή οι ασυμπτωτικές διευθύνσεις διχοτομούνται από τις κύριες διευθύνσεις (όπως δείχνει το σύστημα αναφοράς μας  ).
).
Το υπερβολικό σημείο εξασφαλίζει την ύπαρξη ακριβώς δύο ασυμπτωτικών διευθύνσεων (για παραβολικά και άλλα σημεία οι διευθύνσεις μπορεί να είναι άπειρες, μία ή καμία)
 μοναδιαία διανύσματα προς τις δυό κύριες διευθύνσεις και
μοναδιαία διανύσματα προς τις δυό κύριες διευθύνσεις και  η γωνία που διαγράφει μια ασυμπτωτική διεύθυνση με μία κύρια διεύθυνση (wlog.
η γωνία που διαγράφει μια ασυμπτωτική διεύθυνση με μία κύρια διεύθυνση (wlog.  ) τότε από τον τύπο Euler για την κάθετη καμπυλότητα (αυτόν εδώ)
) τότε από τον τύπο Euler για την κάθετη καμπυλότητα (αυτόν εδώ) 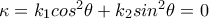 αφού βρισκόμαστε σε ασυμπτωτική διεύθυνση. Άρα
αφού βρισκόμαστε σε ασυμπτωτική διεύθυνση. Άρα  (το σημείο είναι υπερβολικό επομένως η Gaussian
(το σημείο είναι υπερβολικό επομένως η Gaussian  ) και
) και  , επομένως οι γωνίες
, επομένως οι γωνίες  βρίσκονται επίσης σε ασυμπτωτικές διευθύνσεις, δηλαδή οι ασυμπτωτικές διευθύνσεις διχοτομούνται από τις κύριες διευθύνσεις (όπως δείχνει το σύστημα αναφοράς μας
βρίσκονται επίσης σε ασυμπτωτικές διευθύνσεις, δηλαδή οι ασυμπτωτικές διευθύνσεις διχοτομούνται από τις κύριες διευθύνσεις (όπως δείχνει το σύστημα αναφοράς μας  ).
).Το υπερβολικό σημείο εξασφαλίζει την ύπαρξη ακριβώς δύο ασυμπτωτικών διευθύνσεων (για παραβολικά και άλλα σημεία οι διευθύνσεις μπορεί να είναι άπειρες, μία ή καμία)
- grigkost
- Διαχειριστής
- Δημοσιεύσεις: 3053
- Εγγραφή: Πέμ Δεκ 18, 2008 12:54 pm
- Τοποθεσία: Ιωάννινα
- Επικοινωνία:
Re: Υπερβολικό σημείο επιφάνειας
Στο "ίδιο μήκος κύματος" με την απόδειξη του τύπου για κάθετη καμπυλότητα:
Έστω τυχόν υπερβολικό σημείο στην επιφάνεια
τυχόν υπερβολικό σημείο στην επιφάνεια  ; επομένως
; επομένως  και υπάρχουν ακριβώς δύο ασυμπτωτικές διευθύνσεις στο
και υπάρχουν ακριβώς δύο ασυμπτωτικές διευθύνσεις στο  . Έστω
. Έστω  η αντίστοιχη ιδιοβάση του
η αντίστοιχη ιδιοβάση του 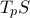 . Τότε για τυχούσα διεύθυνση
. Τότε για τυχούσα διεύθυνση  με
με  και
και  την γωνία που σχηματίζουν τα
την γωνία που σχηματίζουν τα  , ισχύει
, ισχύει

Έστωσαν οι ασυμπτωτικές διευθύνσεις στο
οι ασυμπτωτικές διευθύνσεις στο  και
και  οι αντίστοιχες γωνίες που σχηματίζουν με το
οι αντίστοιχες γωνίες που σχηματίζουν με το  .
.
Τότε

Επίσης, επειδή , έπεται ότι και οι γωνίες που σχηματίζουν τα
, έπεται ότι και οι γωνίες που σχηματίζουν τα  με το
με το  είναι ίσες ή παραπληρωματικές. Άρα οι κύριες διευθύνσεις διχοτομούν τις ασυμπτωτικές διευθύνσεις σε τυχόν υπερβολικό σημείο μιας επιφάνειας.
είναι ίσες ή παραπληρωματικές. Άρα οι κύριες διευθύνσεις διχοτομούν τις ασυμπτωτικές διευθύνσεις σε τυχόν υπερβολικό σημείο μιας επιφάνειας.
Έστω
 τυχόν υπερβολικό σημείο στην επιφάνεια
τυχόν υπερβολικό σημείο στην επιφάνεια  ; επομένως
; επομένως  και υπάρχουν ακριβώς δύο ασυμπτωτικές διευθύνσεις στο
και υπάρχουν ακριβώς δύο ασυμπτωτικές διευθύνσεις στο  . Έστω
. Έστω  η αντίστοιχη ιδιοβάση του
η αντίστοιχη ιδιοβάση του 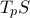 . Τότε για τυχούσα διεύθυνση
. Τότε για τυχούσα διεύθυνση  με
με  και
και  την γωνία που σχηματίζουν τα
την γωνία που σχηματίζουν τα  , ισχύει
, ισχύει 
Έστωσαν
 οι ασυμπτωτικές διευθύνσεις στο
οι ασυμπτωτικές διευθύνσεις στο  και
και  οι αντίστοιχες γωνίες που σχηματίζουν με το
οι αντίστοιχες γωνίες που σχηματίζουν με το  .
.Τότε

Επίσης, επειδή
 , έπεται ότι και οι γωνίες που σχηματίζουν τα
, έπεται ότι και οι γωνίες που σχηματίζουν τα  με το
με το  είναι ίσες ή παραπληρωματικές. Άρα οι κύριες διευθύνσεις διχοτομούν τις ασυμπτωτικές διευθύνσεις σε τυχόν υπερβολικό σημείο μιας επιφάνειας.
είναι ίσες ή παραπληρωματικές. Άρα οι κύριες διευθύνσεις διχοτομούν τις ασυμπτωτικές διευθύνσεις σε τυχόν υπερβολικό σημείο μιας επιφάνειας.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
