Μεταφέροντας αν είναι ανάγκη την καμπύλη μπορούμε να υποθέσουμε ότι

Παραγωγίζοντας παίρνουμε

Αν

είναι το τρίεδρο Frenet θα έχουμε

(1)
οπου
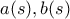
πραγματικές συναρτήσεις,με

(2)
Ενα γνωστό επιχείρημα μας δίνει ότι παραγωγίζονται .
Παραγωγίζοντας την (1) χρησιμοποιώντας τις σχέσεις του Frenet και το γεγονός ότι
τα

είναι γραμμικώς ανεξάρτητα παίρνουμε ότι

Από τις δύο πρώτες αν κάνουμε αντικατάσταση στην (2) παίρνουμε

(3)
που είναι η ζητούμενη σχέση.
Αντίστροφα ,έστω ότι ισχύει η (3).
Θεωρούμε την καμπύλη

(4)
Παραγωγίζοντας και χρησιμοποιώντας τις σχέσεις του Frenet παίρνουμε ότι

Αλλά αν παραγωγίσουμε την (3) και χρησιμοποιήσουμε αυτά που δεν μηδενίζονται πα'ιρνουμε
ότι

Αρα

οπότε η (4) δίνει

που δείχνει ότι η καμπύλη είναι σφαιρική.
 μια φυσική παραμέτρηση καμπύλης για την οποία, για κάθε
μια φυσική παραμέτρηση καμπύλης για την οποία, για κάθε  , ισχύουν
, ισχύουν  και
και  , όπου
, όπου  η καμπυλότητα και
η καμπυλότητα και  η στρέψη της καμπύλης. Να αποδειχθεί ότι ικανή και αναγκαία συνθήκη για να βρίσκεται η καμπύλη πάνω σε μια σφαίρα είναι
η στρέψη της καμπύλης. Να αποδειχθεί ότι ικανή και αναγκαία συνθήκη για να βρίσκεται η καμπύλη πάνω σε μια σφαίρα είναι 





 είναι το τρίεδρο Frenet θα έχουμε
είναι το τρίεδρο Frenet θα έχουμε  (1)
(1)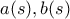 πραγματικές συναρτήσεις,με
πραγματικές συναρτήσεις,με  (2)
(2)
 (3)
(3) (4)
(4)



 και ακτίνα
και ακτίνα  . Τότε
. Τότε 
 έχουμε ότι το διάνυσμα
έχουμε ότι το διάνυσμα  βρίσκεται στο κάθετο επίπεδο της
βρίσκεται στο κάθετο επίπεδο της  . Επομένως
. Επομένως 
 η γωνία που σχηματίζει το
η γωνία που σχηματίζει το  με το
με το  .
. και
και  , προκύπτουν
, προκύπτουν  και
και  , αντίστοιχα. Άρα η
, αντίστοιχα. Άρα η  γίνεται
γίνεται 
 και την
και την  προκύπτει ότι
προκύπτει ότι 
 . Τότε
. Τότε 
 με τύπο
με τύπο 



 βρίσκεται πάνω σε σφαίρα με κέντρο το πέρας του
βρίσκεται πάνω σε σφαίρα με κέντρο το πέρας του