Ανισότητα

Tolaso J Kos · #1

Έστω ο $\mathbb{R}^n$ με το σύνηθες γινόμενο και τη συνήθη νόρμα. Αν $v = (x_1, x_2, \dots, x_n) \in \mathbb{R}^n$ τότε ορίζουμε $\sum v = x_1 +x_2 + \cdots + x_n$ . Να δειχθεί ότι:

$\displaystyle{\left \| v \right \|^2 \left \| w \right \|^2 \geq \left ( v \cdot w \right )^2 + \frac{\left ( \left \| v \right \| \left | \sum w \right | - \left \| w \right \| \left |\sum v \right | \right )^2}{n}}$

#2

Tolaso J Kos έγραψε: ↑
Τετ Οκτ 28, 2020 9:22 am
Έστω ο $\mathbb{R}^n$ με το σύνηθες γινόμενο και τη συνήθη νόρμα. Αν $v = (x_1, x_2, \dots, x_n) \in \mathbb{R}^n$ τότε ορίζουμε $\sum v = x_1 +x_2 + \cdots + x_n$ . Να δειχθεί ότι:

$\displaystyle{\left \| v \right \|^2 \left \| w \right \|^2 \geq \left ( v \cdot w \right )^2 + \frac{\left ( \left \| v \right \| \left | \sum w \right | - \left \| w \right \| \left |\sum v \right | \right )^2}{n}}$

Απίθανη ενδυνάμωση της ανισότητας Cauchy-Schwarz -- ορθώς (υπο)γράφει ο Τόλης ότι "η φαντασία είναι ανώτερη από την γνώση" -- που σεμνά και ταπεινά επαναφέρω ... με απλή (φαινομενικά) απόδειξη για n=2

:

Αν

,

τότε η ζητούμενη ανισότητα είναι ισοδύναμη προς την προφανώς ισχύουσα

$\left[(ad-bc)(a+b)(c+d)\right]^2\geq 0.$
[Ας συγκριθεί αυτή η ανισότητα με την ανισότητα $(ad-bc)^2\geq 0$ που δίνει την Cauchy-Schwarz για n=2

... και ας μας εμπνεύσει για απόδειξη της ζητούμενης ανισότητας για n>2

]

Tolaso J Kos · #3

Γιώργο θα σε εκπλήξω λέγοντας σε ότι είναι ειδική περίπτωση γενικότερης ανισότητας ...

Tolaso J Kos · #4

Θα δείξουμε τη γενικότερη ...

$\displaystyle{\left ( \left \| v \right \|^2 \left \| w \right \|^2 - \left ( v \cdot w \right )^2 \right ) \left \| u \right \|^2 \geq \left \| \left ( w, u \right ) v - \left ( v, u \right ) w \right \|^2}$
όπου $u \in \mathbb{R}^{n}$ . Παίρνοντας $u=(1, 1 , \dots, 1)$ μας δίδει τη ζητούμενη. Αν v, w

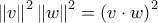είναι γραμμικά εξαρτημένα τότε $\left \| v \right \|^2 \left \| w \right \|^2 = \left ( v \cdot w \right )^2$ η ανισότητα ισχύει. Υποθέτουμε ότι τα

και

είναι γραμμικά ανεξάρτητα. Τότε $u = \alpha v + \beta w + z$ όπου $\alpha, \beta \in \mathbb{R}$ και $z \perp v$ , $z \perp w$ . Επιπλέον,

$\displaystyle{\left\{\begin{matrix} \left ( v, u \right ) & = & \alpha \left \| v \right \|^2 + \beta \left ( v, w \right ) \\\\ \left ( w, u \right ) & = & \alpha \left ( v, w \right ) + \beta \left \| w \right \|^2 \end{matrix}\right.}$
Λύνοντας το γραμμικό σύστημα έχουμε

$\displaystyle{\alpha = \frac{\left ( v, u \right ) \left \| w \right \|^2 - \left ( w, u \right ) \left ( v, w \right )}{\left \| v \right \|^2 \left \| w \right \|^2 - \left ( v, w \right )^2} \quad , \quad \beta = \frac{\left ( w, u \right )\left \| u \right \|^2 - \left ( v, u \right )\left ( v, w \right )}{\left \| v \right \|^2 \left \| w \right \|^2 - \left ( v, w \right )^2}}$
Οπότε,

$\displaystyle{\begin{aligned} \left ( \left \| v \right \|^2 \left \| w \right \|^2 - \left ( v \cdot w \right )^2 \right ) \left \| u \right \|^2 &= \left ( \left \| v \right \|^2 \left \| w \right \|^2 - \left ( v \cdot w \right )^2 \right ) \left ( \left \| \alpha v + \beta w \right \|^2 + \left \| z \right \|^2 \right ) \\ &\geq \left ( \left \| v \right \|^2 \left \| w \right \|^2 - \left ( v \cdot w \right )^2 \right ) \left ( \left \| \alpha v + \beta w \right \|^2 \right ) \\ &= \left ( \left \| v \right \|^2 \left \| w \right \|^2 - \left ( v \cdot w \right )^2 \right ) \left ( \alpha^2 \left \| v \right \|^2 + \beta^2 \left \| w \right \|^2 + 2\alpha \beta \left ( v, w \right ) \right ) \\ &= \left ( w, u \right )^2 \left \| v \right \|^2 + \left ( v, u \right ) \left \| w \right \|^2 - 2 \left ( w, u \right ) \left ( v,u \right ) \left ( v, w \right ) \\ &= \left \| \left ( w, u \right ) v - \left ( v, u \right )w \right \|^2 \end{aligned}}$

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #5

Tolaso J Kos έγραψε: ↑
Κυρ Απρ 04, 2021 11:31 am
Θα δείξουμε τη γενικότερη ...

$\displaystyle{\left ( \left \| v \right \|^2 \left \| w \right \|^2 - \left ( v \cdot w \right )^2 \right ) \left \| u \right \|^2 \geq \left \| \left ( w, u \right ) v - \left ( v, u \right ) w \right \|^2}$

Σχεδόν τετριμμένη αν ξέρεις τι να κάνεις.
1)Αρκεί να την δείξουμε όταν $u,v,w\in \mathbb{R}^3$
(γιατί ; )
2) Αλλάζοντας συντεταγμένες και λόγω ομογενειας αρκεί να πάρουμε v=(1,0,0)

3)Αν θεωρήσουμε τα u,w

με τις συντεταγμένες τους και αντικαταστήσουμε το μόνο που
χρειάζεται είναι μια C-S και μάλιστα για δύο μεταβλητές.

#6

Tolaso J Kos έγραψε: ↑
Κυρ Απρ 04, 2021 11:31 am
Αν είναι γραμμικά εξαρτημένα τότε $\left \| v \right \|^2 \left \| w \right \|^2 = \left ( v \cdot w \right )^2$ η ανισότητα ισχύει.

Άσκηση: Βρες το λογικό σφάλμα στο παραπάνω βήμα.

(Ευτυχώς, φτιάχνει).

Ανισότητα

Ανισότητα

Re: Ανισότητα

Re: Ανισότητα

Re: Ανισότητα

Re: Ανισότητα

Re: Ανισότητα

Μέλη σε σύνδεση