 στον
στον  . Μπορούμε να βρούμε ένα σύνολο
. Μπορούμε να βρούμε ένα σύνολο  (πιθανόν κυρτό) ώστε να ισχύουν τα ακόλουθα ταυτόχρονα;
(πιθανόν κυρτό) ώστε να ισχύουν τα ακόλουθα ταυτόχρονα;(1)
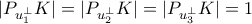
(2)
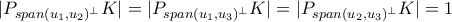
(3)
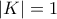
Συντονιστής: matha
 στον
στον  . Μπορούμε να βρούμε ένα σύνολο
. Μπορούμε να βρούμε ένα σύνολο  (πιθανόν κυρτό) ώστε να ισχύουν τα ακόλουθα ταυτόχρονα;
(πιθανόν κυρτό) ώστε να ισχύουν τα ακόλουθα ταυτόχρονα;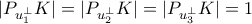
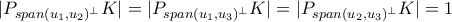
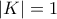
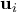 είναι μοναδιαία. Θεωρώ όλα τα
είναι μοναδιαία. Θεωρώ όλα τα  ώστε
ώστε ![\mathbf{v} \cdot \mathbf{u}_i \in [0,1] \mathbf{v} \cdot \mathbf{u}_i \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c330cbac759cbab34460a3359ffb722c.png) και παίρνω το
και παίρνω το  να είναι το σύνολο αυτών των
να είναι το σύνολο αυτών των  .
.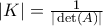 όπου
όπου 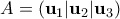 . Πράγματι αυτό είναι συνέπεια της παρατήρησης ότι
. Πράγματι αυτό είναι συνέπεια της παρατήρησης ότι 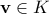 αν και μόνο αν
αν και μόνο αν ![\mathbf{v}^T A \in [0,1]^3 \mathbf{v}^T A \in [0,1]^3](/forum/ext/geomar/texintegr/latexrender/pictures/0f4bcad964214b2f218fe03d326fe0a0.png) .
. 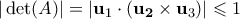 . Άρα
. Άρα 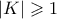 .
. 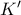 του
του  ώστε
ώστε 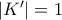 . Τώρα μπορεί να χάλασα τις (1) και (2). Αυτό όμως διορθώνεται εύκολα. Μπορώ να προσθέσω ένα σύνολο μηδενικού όγκου ώστε όλες οι προβολές να γίνουν ξανά ίσες με 1.
. Τώρα μπορεί να χάλασα τις (1) και (2). Αυτό όμως διορθώνεται εύκολα. Μπορώ να προσθέσω ένα σύνολο μηδενικού όγκου ώστε όλες οι προβολές να γίνουν ξανά ίσες με 1.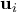 δεν είναι γραμμικώς ανεξάρτητα. Σε αυτήν την περίπτωση θα έχουμε αρχικά
δεν είναι γραμμικώς ανεξάρτητα. Σε αυτήν την περίπτωση θα έχουμε αρχικά 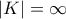 αλλά αυτό δεν διαφοροποιεί το επιχείρημα. Απλά θέλουμε τα διανύσματα να μην είναι μηδενικά ώστε να έχουν νόημα οι προβολές.]
αλλά αυτό δεν διαφοροποιεί το επιχείρημα. Απλά θέλουμε τα διανύσματα να μην είναι μηδενικά ώστε να έχουν νόημα οι προβολές.]Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες