Αν
 και
και  με
με  , να αποδειχθεί ότι :
, να αποδειχθεί ότι :
Μπάμπης
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 και, λαμβάνοντας υπ' όψιν τη συνθήκη, παίρνουμε το ζητούμενο.
και, λαμβάνοντας υπ' όψιν τη συνθήκη, παίρνουμε το ζητούμενο.
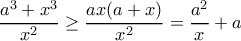 .
.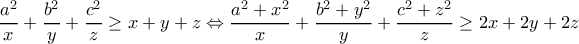 .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες