 .
.Αναζήτηση δεκαδικών ψηφίων
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Αναζήτηση δεκαδικών ψηφίων
Να βρείτε τα πρώτα 2016 ψηφία, μετά την υποδιαστολή, της δεκαδικής αναπαράσταση του αριθμού
 .
.
 .
.
τελευταία επεξεργασία από Al.Koutsouridis σε Τρί Σεπ 27, 2016 2:13 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Αναζήτηση δεκαδικών ψηφίων
Απάντηση στο ενδιαφέρον αυτό ερώτημα: Και ταAl.Koutsouridis έγραψε:Να βρείτε τα πρώτα 2016 ψηφία, μετά την υποδιαστολή, της δεκαδικής αναπαράσταση του αριθμού
.
 ψηφία είναι εννιάρια.
ψηφία είναι εννιάρια.Από το ανάπτυγμα του διωνύμου εύκολα βλέπουμε ότι ο αριθμός
 είναι ακέραιος. Πράγματι α) οι συντελεστές στο ανάπτυγμα
είναι ακέραιος. Πράγματι α) οι συντελεστές στο ανάπτυγμα  είναι ακέραιοι και β) οι μεν άρτιες δυνάμεις του
είναι ακέραιοι και β) οι μεν άρτιες δυνάμεις του  είναι ακέραιες οι δε περιττές απλοποιούνται ανά ζεύγη ως αντίθετοι αριθμοί. Στον ισολογισμό μένει μόνο ένα άθροισμα ακεραίων.
είναι ακέραιες οι δε περιττές απλοποιούνται ανά ζεύγη ως αντίθετοι αριθμοί. Στον ισολογισμό μένει μόνο ένα άθροισμα ακεραίων.Συμπεραίνουμε ότι ο
 ισούται με "ακέραιο πλην
ισούται με "ακέραιο πλην  .
.Όμως
 οπότε
οπότε  , από όπου το ζητούμενο.
, από όπου το ζητούμενο.- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Αναζήτηση δεκαδικών ψηφίων
Ας βρεθεί και από πάσα εννιάρια ξεκινάει αυτός ο αριθμός. [Επιτρέπεται η χρήση υπολογιστικής.]
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Αναζήτηση δεκαδικών ψηφίων
Το αποσύρω προσωρινά γιατί έχω λογιστικό σφάλμα στις πράξεις (η μέθοδος σωστή)  . Θα επανέλθω, αλλά υπομονή γιατί σήμερα έχω βαρύ πρόγραμμα.
. Θα επανέλθω, αλλά υπομονή γιατί σήμερα έχω βαρύ πρόγραμμα.
Ζητώ συγνώμη για την ταλαιπωρία.
Ζητώ συγνώμη για την ταλαιπωρία.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Αναζήτηση δεκαδικών ψηφίων
Επανέρχομαι αλλά με πιο προσεκτικό έλεγχο των πράξεων.
Θα δείξουμε ότι τα εννιάρια είναι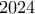 (το ψηφίο στην θέση
(το ψηφίο στην θέση  δεν είναι εννιάρι αλλά δεν ξέρω ποιο ακριβώς από τα ψηφία
δεν είναι εννιάρι αλλά δεν ξέρω ποιο ακριβώς από τα ψηφία  έως
έως  είναι τούτο).
είναι τούτο).
Εύκολα βλέπουμε ότι . Για παράδειγμα το κομπιουτεράκι δείχνει
. Για παράδειγμα το κομπιουτεράκι δείχνει  αλλά μπορούμε και χωρίς κομπιουτεράκι να διαπιστώσουμε την ανισότητα με ύψωση στο τετράγωνο αφού πάμε το
αλλά μπορούμε και χωρίς κομπιουτεράκι να διαπιστώσουμε την ανισότητα με ύψωση στο τετράγωνο αφού πάμε το  στο άλλο μέλος.
στο άλλο μέλος.
Άρα

Θα δείξουμε ότι

οπότε σε συνδυασμό την εκτίμηση στο προηγούμενο ποστ έχουμε, για κάποιον φυσικό ,
,

από όπου το ζητούμενο.
Μένει να δείξουμε τις οι οποίες ισοδυναμούν με
οι οποίες ισοδυναμούν με

Κατά το κομπιουτεράκι μου η παραπάνω αληθεύει αφού γράφεται
 (αληθής).
(αληθής).
Ελπίζω αυτή την φορά να μην έκανα κάπου λάθος πράξεις. Όπως και να είναι, η διαδικασία φαίνεται σωστή και εύκολα προσαρμόζεται σε πιο προσεκτικές πράξεις, αν οι παραπάνω είναι λανθασμένες.
Ας προσθέσω ότι το κομπιουτεράκι δεν είναι απαραίτητο. Για παράδειγμα για τον λογάριθμο του που εμφανίζεται, μας χρειάζονται μόνον τα
που εμφανίζεται, μας χρειάζονται μόνον τα  . Αυτά μπορούν να γίνουν με το χέρι, με πολύ μεγάλη ακρίβεια. Σύντομα θα αναρτήσω ένα άρθρο μου του
. Αυτά μπορούν να γίνουν με το χέρι, με πολύ μεγάλη ακρίβεια. Σύντομα θα αναρτήσω ένα άρθρο μου του  (... σωστά διαβάσατε...) που είχα δημοσιεύσει στον Ευκλείδη Γ' , όπου περιέχει ιστορία ωραιότατων μεθόδων υπολογισμού λογαρίθμων μικρών ακεραίων.
(... σωστά διαβάσατε...) που είχα δημοσιεύσει στον Ευκλείδη Γ' , όπου περιέχει ιστορία ωραιότατων μεθόδων υπολογισμού λογαρίθμων μικρών ακεραίων.
Φιλικά,
Μιχάλης
Καλό.Demetres έγραψε:Ας βρεθεί και από πάσα εννιάρια ξεκινάει αυτός ο αριθμός. [Επιτρέπεται η χρήση υπολογιστικής.]
Θα δείξουμε ότι τα εννιάρια είναι
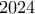 (το ψηφίο στην θέση
(το ψηφίο στην θέση  δεν είναι εννιάρι αλλά δεν ξέρω ποιο ακριβώς από τα ψηφία
δεν είναι εννιάρι αλλά δεν ξέρω ποιο ακριβώς από τα ψηφία  έως
έως  είναι τούτο).
είναι τούτο). Εύκολα βλέπουμε ότι
 . Για παράδειγμα το κομπιουτεράκι δείχνει
. Για παράδειγμα το κομπιουτεράκι δείχνει  αλλά μπορούμε και χωρίς κομπιουτεράκι να διαπιστώσουμε την ανισότητα με ύψωση στο τετράγωνο αφού πάμε το
αλλά μπορούμε και χωρίς κομπιουτεράκι να διαπιστώσουμε την ανισότητα με ύψωση στο τετράγωνο αφού πάμε το  στο άλλο μέλος.
στο άλλο μέλος.Άρα

Θα δείξουμε ότι

οπότε σε συνδυασμό την εκτίμηση στο προηγούμενο ποστ έχουμε, για κάποιον φυσικό
 ,
, 
από όπου το ζητούμενο.
Μένει να δείξουμε τις
 οι οποίες ισοδυναμούν με
οι οποίες ισοδυναμούν με 
Κατά το κομπιουτεράκι μου η παραπάνω αληθεύει αφού γράφεται
 (αληθής).
(αληθής).Ελπίζω αυτή την φορά να μην έκανα κάπου λάθος πράξεις. Όπως και να είναι, η διαδικασία φαίνεται σωστή και εύκολα προσαρμόζεται σε πιο προσεκτικές πράξεις, αν οι παραπάνω είναι λανθασμένες.
Ας προσθέσω ότι το κομπιουτεράκι δεν είναι απαραίτητο. Για παράδειγμα για τον λογάριθμο του
 που εμφανίζεται, μας χρειάζονται μόνον τα
που εμφανίζεται, μας χρειάζονται μόνον τα  . Αυτά μπορούν να γίνουν με το χέρι, με πολύ μεγάλη ακρίβεια. Σύντομα θα αναρτήσω ένα άρθρο μου του
. Αυτά μπορούν να γίνουν με το χέρι, με πολύ μεγάλη ακρίβεια. Σύντομα θα αναρτήσω ένα άρθρο μου του  (... σωστά διαβάσατε...) που είχα δημοσιεύσει στον Ευκλείδη Γ' , όπου περιέχει ιστορία ωραιότατων μεθόδων υπολογισμού λογαρίθμων μικρών ακεραίων.
(... σωστά διαβάσατε...) που είχα δημοσιεύσει στον Ευκλείδη Γ' , όπου περιέχει ιστορία ωραιότατων μεθόδων υπολογισμού λογαρίθμων μικρών ακεραίων.Φιλικά,
Μιχάλης
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Αναζήτηση δεκαδικών ψηφίων
Σωστά.
Αν θέλουμε να βρούμε και επόμενα ψηφία πάλι μπορούμε να χρησιμοποιήσουμε λογαρίθμους. Π.χ. η υπολογιστική μου, μου λέει ότι

Μπορώ λοιπόν να χρησιμοποιήσω ότι![\displaystyle{ 2016\log_{10}(\sqrt{26}-5) \in [-2024.63,-2024.62]\ldots} \displaystyle{ 2016\log_{10}(\sqrt{26}-5) \in [-2024.63,-2024.62]\ldots}](/forum/ext/geomar/texintegr/latexrender/pictures/302f8b6568935df9b6262a54cab9dbc9.png) για να πάρω
για να πάρω

Οπότε μετά τα εννιάρια το επόμενο ψηφίο είναι
εννιάρια το επόμενο ψηφίο είναι  και το μεθεπόμενο
και το μεθεπόμενο  . Το επόμενο είναι μεταξύ του
. Το επόμενο είναι μεταξύ του  με του
με του  και μπορεί να υπολογιστεί με τον ίδιο τρόπο.
και μπορεί να υπολογιστεί με τον ίδιο τρόπο.
Αν θέλουμε να βρούμε και επόμενα ψηφία πάλι μπορούμε να χρησιμοποιήσουμε λογαρίθμους. Π.χ. η υπολογιστική μου, μου λέει ότι

Μπορώ λοιπόν να χρησιμοποιήσω ότι
![\displaystyle{ 2016\log_{10}(\sqrt{26}-5) \in [-2024.63,-2024.62]\ldots} \displaystyle{ 2016\log_{10}(\sqrt{26}-5) \in [-2024.63,-2024.62]\ldots}](/forum/ext/geomar/texintegr/latexrender/pictures/302f8b6568935df9b6262a54cab9dbc9.png) για να πάρω
για να πάρω 
Οπότε μετά τα
 εννιάρια το επόμενο ψηφίο είναι
εννιάρια το επόμενο ψηφίο είναι  και το μεθεπόμενο
και το μεθεπόμενο  . Το επόμενο είναι μεταξύ του
. Το επόμενο είναι μεταξύ του  με του
με του  και μπορεί να υπολογιστεί με τον ίδιο τρόπο.
και μπορεί να υπολογιστεί με τον ίδιο τρόπο.- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Αναζήτηση δεκαδικών ψηφίων
Ευχαριστώ τους κ.Λάμπρου και Δημήτρη για την λύση και τις γενικεύσεις. Για την ιστορία να αναφέρω ότι το πρόβλημα είναι από την Μαθηματική Ολυμπιάδα Α.Πετρούπολης(1963). Στην περίπτωση που ο εκθέτης είναι περιττός μπορούμε να εραγστούμε με παρόμοιο τρόπο και να δείξουμε οτι τα πρώτα ψηφία μετα την υποδιαστολή είναι μηδενικά.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
