Αν οι θετικοί πραγματικοί αριθμοί
 ικανοποιούν την
ικανοποιούν την  να αποδείξετε ότι
να αποδείξετε ότι 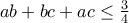
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 ικανοποιούν την
ικανοποιούν την  να αποδείξετε ότι
να αποδείξετε ότι 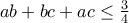
 το προς απόδειξη γίνεται
το προς απόδειξη γίνεται  .
.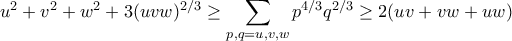 .
.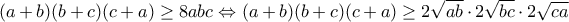
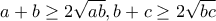 και
και 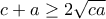 .
. 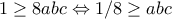 (1).
(1).
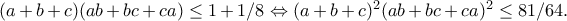
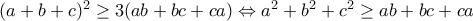 που ισχύει, αφού πρόκειται για γνωστή ανισότητα.
που ισχύει, αφού πρόκειται για γνωστή ανισότητα.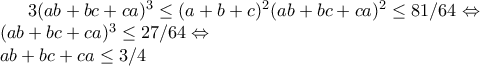
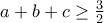 αφού τότε
αφού τότε  .
.![2(a+b+c)=(a+b)+(b+c)+(c+a)\geq 3\sqrt[3]{(a+b)^2(b+c)^2(a+c)^2}=3\Rightarrow a+b+c\geq \frac{3}{2} 2(a+b+c)=(a+b)+(b+c)+(c+a)\geq 3\sqrt[3]{(a+b)^2(b+c)^2(a+c)^2}=3\Rightarrow a+b+c\geq \frac{3}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/179f5e86193492723ea0ea5c69c223c2.png) ,το ζητούμενο.
,το ζητούμενο. Για θετικούς
Για θετικούς  ισχύει
ισχύει![\displaystyle{\sqrt[3]{\frac{(a+b)(b+c)(c+a)}{8}}\geq \sqrt{\frac{ab+bc+ca}{3}}} \displaystyle{\sqrt[3]{\frac{(a+b)(b+c)(c+a)}{8}}\geq \sqrt{\frac{ab+bc+ca}{3}}}](/forum/ext/geomar/texintegr/latexrender/pictures/fb1eb3cb18db3757ed501b4324101cb3.png) .
.![\displaystyle{(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)-abc=(a+b+c)(ab+bc+ca)-\sqrt[3]{abc}\sqrt[3]{(abc)^2}\geq } \displaystyle{(a+b)(b+c)(c+a)=(a+b+c)(ab+bc+ca)-abc=(a+b+c)(ab+bc+ca)-\sqrt[3]{abc}\sqrt[3]{(abc)^2}\geq }](/forum/ext/geomar/texintegr/latexrender/pictures/eb3c6fd2a5190018156537e585432503.png)

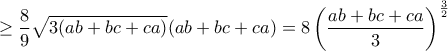
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης