 , να λύσετε στο
, να λύσετε στο  το σύστημα
το σύστημα  .
.Ορέστης
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
Γεια σου Ορέστη.orestis26 έγραψε:Αν, να λύσετε στο
το σύστημα
.
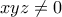 .
.  που με χρήση της πρώτης στην μορφή
που με χρήση της πρώτης στην μορφή  γίνεται
γίνεται  . H τελευταία γράφεται
. H τελευταία γράφεται  (είναι δευτεροβάθμια ως προς
(είναι δευτεροβάθμια ως προς  οπότε δεν έχουμε πρόβλημα να την παραγοντοποιήσουμε).
οπότε δεν έχουμε πρόβλημα να την παραγοντοποιήσουμε). ή
ή  ή
ή 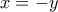
 στην πρώτη εξίσωση δίνει
στην πρώτη εξίσωση δίνει 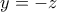 δηλαδή έχουμε λύση της μορφής
δηλαδή έχουμε λύση της μορφής  . Οι υπόλοιπες οδηγούν σε όμοιες λύσεις με κυκλική εναλλαγή, οπότε ας μείνουμε στις λύσεις της μορφής
. Οι υπόλοιπες οδηγούν σε όμοιες λύσεις με κυκλική εναλλαγή, οπότε ας μείνουμε στις λύσεις της μορφής  .
. , άρα
, άρα  (που είναι δεκτή εκτός αν
(που είναι δεκτή εκτός αν  που απορρίπτεται λόγω του περιορισμού). Τελικά μία λύση είναι η
που απορρίπτεται λόγω του περιορισμού). Τελικά μία λύση είναι η  . Και λοιπά.
. Και λοιπά.  είναι
είναι 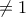 .
. λόγω της πρώτης και δεύτερης εξίσωσης του συστήματος αντίστοιχα.
λόγω της πρώτης και δεύτερης εξίσωσης του συστήματος αντίστοιχα.
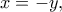 από την τρίτη εξίσωση βρίσκουμε
από την τρίτη εξίσωση βρίσκουμε οπότε λύση του συστήματος είναι η τριάδα
οπότε λύση του συστήματος είναι η τριάδα
 είναι ρίζες πολυωνύμου της μορφής
είναι ρίζες πολυωνύμου της μορφής  , που έχει πάντα ρίζα το
, που έχει πάντα ρίζα το  . Στη συνέχεια παίρνουμε τις τρεις περιπτώσεις
. Στη συνέχεια παίρνουμε τις τρεις περιπτώσεις  και λύνουμε την τρίτη εξίσωση, προσέχοντας να απορρίψουμε τις μηδενικές λύσεις.
και λύνουμε την τρίτη εξίσωση, προσέχοντας να απορρίψουμε τις μηδενικές λύσεις.orestis26 έγραψε:Αν, να λύσετε στο
το σύστημα
.
Ορέστης
 με
με  οπότε προφανώς
οπότε προφανώς 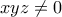
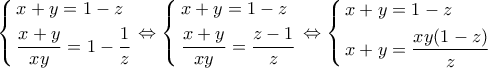 . Εξισώνουμε τα δεύτερα μέλη και έχουμε:
. Εξισώνουμε τα δεύτερα μέλη και έχουμε: .
.  . Θα μελετήσουμε την πρώτη περίπτωση
. Θα μελετήσουμε την πρώτη περίπτωση  και μετά με προσεκτική εναλλαγή αγνώστων αλλά και παραμέτρων θα έχουμε την πλήρη λύση.
και μετά με προσεκτική εναλλαγή αγνώστων αλλά και παραμέτρων θα έχουμε την πλήρη λύση. λοιπόν έχουμε δύο περιπτώσεις :
λοιπόν έχουμε δύο περιπτώσεις : 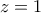 ή
ή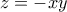 .
. που επαληθεύει τη
που επαληθεύει τη  και άρα είναι μια λύση του αρχικού .
και άρα είναι μια λύση του αρχικού .
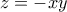 τότε ή
τότε ή  δίδει
δίδει  που γράφεται
που γράφεται  . Οπότε:
. Οπότε: που είναι ή περίπτωση
που είναι ή περίπτωση  , είτε
, είτε  δηλαδή
δηλαδή  και προκύπτει το σύστημα :
και προκύπτει το σύστημα : που όμως δεν επαληθεύει τη
που όμως δεν επαληθεύει τη  .
.Και "άλλη" μία λύση. Ουσιαστικά είναι παραλλαγή των προηγούμενων, αλλά ντυμένη αλλιώς.orestis26 έγραψε:Αν, να λύσετε στο
το σύστημα
.
 . Παρατηρούμε τώρα, με χρήση αυτών, ότι
. Παρατηρούμε τώρα, με χρήση αυτών, ότι  .
. ισούται με
ισούται με  . Από κει και πέρα το σύστημα είναι απλό, και δεν υπάρχει λόγος να επαναλάβουμε
. Από κει και πέρα το σύστημα είναι απλό, και δεν υπάρχει λόγος να επαναλάβουμε  πραγματικοί (ή μιγαδικοί!) αριθμοί με
πραγματικοί (ή μιγαδικοί!) αριθμοί με  και
και  . Δείξτε ότι τουλάχιστον ένας από αυτούς ισούται με
. Δείξτε ότι τουλάχιστον ένας από αυτούς ισούται με  .
.Μια προσπάθεια στην πολύ ωραία άσκηση που έθεσε ο κ. Λάμπρου.Mihalis_Lambrou έγραψε:Και "άλλη" μία λύση. Ουσιαστικά είναι παραλλαγή των προηγούμενων, αλλά ντυμένη αλλιώς.orestis26 έγραψε:Αν, να λύσετε στο
το σύστημα
.
Οι δύο πρώτες εξισώσεις είναι. Παρατηρούμε τώρα, με χρήση αυτών, ότι
.
Συνεπώς κάποιο από ταισούται με
. Από κει και πέρα το σύστημα είναι απλό, και δεν υπάρχει λόγος να επαναλάβουμε
τα ήδη γραφέντα.
Τολμώ να πω ότι είναι εξ' ίσου ωραία άσκηση αν η αρχική διατυπωθεί ως εξής:
Έστωπραγματικοί (ή μιγαδικοί!) αριθμοί με
και
. Δείξτε ότι τουλάχιστον ένας από αυτούς ισούται με
.


 (1)
(1) , έχουμε ισοδυνάμως :
, έχουμε ισοδυνάμως :  .
. ή
ή  .
. .
.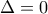

 , οπότε η δευτεροβάθμια παίρνει την μορφή:
, οπότε η δευτεροβάθμια παίρνει την μορφή: 


 , η δευτεροβάθμια έχει δύο ρίζες πραγματικές και άνισες, τις:
, η δευτεροβάθμια έχει δύο ρίζες πραγματικές και άνισες, τις:  και
και  .
.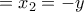 με αντικατάσταση στην (1) προκύπτει
με αντικατάσταση στην (1) προκύπτει  .
. ισούται με
ισούται με  .
.Σταμάτη, θα σου διέφυγε ότι την άσκηση την έχω ήδη λύσει στα παραπάνω.Σταμ. Γλάρος έγραψε:Μια προσπάθεια στην πολύ ωραία άσκηση που έθεσε ο κ. Λάμπρου.
Mihalis_Lambrou έγραψε: Οι δύο πρώτες εξισώσεις είναι. Παρατηρούμε τώρα, με χρήση αυτών, ότι
.
Συνεπώς κάποιο από ταισούται με
.
Καλησπέρα!Mihalis_Lambrou έγραψε:Σταμάτη, θα σου διέφυγε ότι την άσκηση την έχω ήδη λύσει στα παραπάνω.Σταμ. Γλάρος έγραψε:Μια προσπάθεια στην πολύ ωραία άσκηση που έθεσε ο κ. Λάμπρου.
Απομονώνω το σημείο με την εν λόγω λύση:
Mihalis_Lambrou έγραψε: Οι δύο πρώτες εξισώσεις είναι. Παρατηρούμε τώρα, με χρήση αυτών, ότι
.
Συνεπώς κάποιο από ταισούται με
.
 μιγαδικούς!
μιγαδικούς! , αν
, αν  : μιγαδικός.
: μιγαδικός.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες