
Σύστημα με ακεραίους!
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
-
Παύλος Μαραγκουδάκης
- Επιμελητής
- Δημοσιεύσεις: 1513
- Εγγραφή: Παρ Ιαν 30, 2009 1:45 pm
- Τοποθεσία: Πειραιάς
- Επικοινωνία:
Re: Σύστημα με ακεραίους!
Ας είναι  είναι μια λύση του συστήματος.
είναι μια λύση του συστήματος.
 Αν
Αν  τότε
τότε 
 Αν
Αν  τότε
τότε  και
και 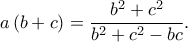
Συνεπώς το κλάσμα είναι ακέραιος και είναι εύκολο να δούμε ότι
είναι ακέραιος και είναι εύκολο να δούμε ότι 
Αν τότε
τότε  δηλαδή
δηλαδή  ή
ή  Για
Για  είναι
είναι  και
και  οπότε
οπότε  και έτσι
και έτσι 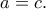 Συνεπώς
Συνεπώς  Ομοίως για
Ομοίως για  βρίσκουμε
βρίσκουμε 
Αν τότε
τότε  Τότε
Τότε  και
και 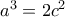 οπότε διαιρώντας
οπότε διαιρώντας  που δεν δίνει ακέραιες λύσεις.
που δεν δίνει ακέραιες λύσεις.
 είναι μια λύση του συστήματος.
είναι μια λύση του συστήματος. Αν
Αν  τότε
τότε 
 Αν
Αν  τότε
τότε  και
και 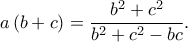
Συνεπώς το κλάσμα
 είναι ακέραιος και είναι εύκολο να δούμε ότι
είναι ακέραιος και είναι εύκολο να δούμε ότι 
Αν
 τότε
τότε  δηλαδή
δηλαδή  ή
ή  Για
Για  είναι
είναι  και
και  οπότε
οπότε  και έτσι
και έτσι 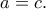 Συνεπώς
Συνεπώς  Ομοίως για
Ομοίως για  βρίσκουμε
βρίσκουμε 
Αν
 τότε
τότε  Τότε
Τότε  και
και 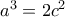 οπότε διαιρώντας
οπότε διαιρώντας  που δεν δίνει ακέραιες λύσεις.
που δεν δίνει ακέραιες λύσεις.Στάλα τη στάλα το νερό το μάρμαρο τρυπά το,
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
- ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
- Δημοσιεύσεις: 921
- Εγγραφή: Πέμ Νοέμ 22, 2018 9:43 pm
Re: Σύστημα με ακεραίους!
Προφανής λύση
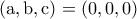 .Είναι
.Είναι  .
. .Άρα δεν μπορεί και οι δύο αρνητικοί.Αν και οι δύο θετικοί τότε
.Άρα δεν μπορεί και οι δύο αρνητικοί.Αν και οι δύο θετικοί τότε 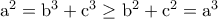 και
και 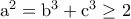 οπότε εύκολα έχουμε άτοπο.
οπότε εύκολα έχουμε άτοπο.Έστω λοιπόν
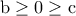 ,θέτω
,θέτω  και η πρώτη σχέση δίνει
και η πρώτη σχέση δίνει  .Έτσι λοιπόν θα πρέπει
.Έτσι λοιπόν θα πρέπει  δηλαδή
δηλαδή  .
.Λύσεις λοιπόν οι
 .
.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
