ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Στο χώρο αυτό θα συνεχίσω με ασκήσεις για Αρχιμήδη Junior και Βαλκανιάδας νέων , αλλά για το 3 επίπεδο.Στο προηγούμενο αντίστοιχο πεδίο J-2 θα έχουμε ασκήσεις για το αμέσως προηγούμενο στάδιο.
Κάθε φορά θα προσθέτω από μία σελίδα ασκήσεων, ώστε να προλαβαίνουμε να τις λύνουμε.
Μπάμπης
Κάθε φορά θα προσθέτω από μία σελίδα ασκήσεων, ώστε να προλαβαίνουμε να τις λύνουμε.
Μπάμπης
- Συνημμένα
-
- ScreenShot004.png (145.23 KiB) Προβλήθηκε 4175 φορές
-
- 0ΑΣΚΗΣΕΙΣ για Ολυμπιάδες J-3.pdf
- (102.67 KiB) Μεταφορτώθηκε 199 φορές
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Για την 8:
Το γινόμενο των αριθμών A είναι

Άρα αρκεί να διαγράψουμε το για να γίνει τέλειο τετράγωνο.
για να γίνει τέλειο τετράγωνο.
Αλέξανδρος
Το γινόμενο των αριθμών A είναι

Άρα αρκεί να διαγράψουμε το
 για να γίνει τέλειο τετράγωνο.
για να γίνει τέλειο τετράγωνο.Αλέξανδρος
Αλέξανδρος Συγκελάκης
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Για το 7:
Θα αποδείξουμε ότι κάθε ένας από τους αριθμούς διαιρεί τον αριθμό
διαιρεί τον αριθμό  για οποιαδήποτε τιμή του
για οποιαδήποτε τιμή του  άρα (επειδή είναι πρώτοι μεταξύ τους) και το γινόμενό τους διαιρεί κάθε ένα από τους αριθμούς.
άρα (επειδή είναι πρώτοι μεταξύ τους) και το γινόμενό τους διαιρεί κάθε ένα από τους αριθμούς.
Διαιρείται από το διότι ο αριθμός
διότι ο αριθμός  διαιρείται από το
διαιρείται από το  . Διαιρείται από το
. Διαιρείται από το  διότι ο αριθμός
διότι ο αριθμός  διαιρείται από το
διαιρείται από το  (Πάρτε περιπτώσεις για το
(Πάρτε περιπτώσεις για το  ).
).
Διαιρείται από το διότι ο αριθμός
διότι ο αριθμός  διαιρείται από το
διαιρείται από το  (Πάρτε περιπτώσεις για το
(Πάρτε περιπτώσεις για το  ). Διαιρείται από το
). Διαιρείται από το  διότι ο αριθμός
διότι ο αριθμός  διαιρείται από το
διαιρείται από το  (Πάρτε περιπτώσεις για το
(Πάρτε περιπτώσεις για το  ) και τέλος διαιρείται από το
) και τέλος διαιρείται από το  διότι ο αριθμός
διότι ο αριθμός  διαιρείται από το
διαιρείται από το  (Πάρτε περιπτώσεις για το
(Πάρτε περιπτώσεις για το  ).
).
Άρα αποκλείεται ο ΜΚΔ να είναι μεγαλύτερος από το .
.
Όμως άρα
άρα
 .
.
Αλέξανδρος
Θα αποδείξουμε ότι κάθε ένας από τους αριθμούς
 διαιρεί τον αριθμό
διαιρεί τον αριθμό  για οποιαδήποτε τιμή του
για οποιαδήποτε τιμή του  άρα (επειδή είναι πρώτοι μεταξύ τους) και το γινόμενό τους διαιρεί κάθε ένα από τους αριθμούς.
άρα (επειδή είναι πρώτοι μεταξύ τους) και το γινόμενό τους διαιρεί κάθε ένα από τους αριθμούς.Διαιρείται από το
 διότι ο αριθμός
διότι ο αριθμός  διαιρείται από το
διαιρείται από το  . Διαιρείται από το
. Διαιρείται από το  διότι ο αριθμός
διότι ο αριθμός  διαιρείται από το
διαιρείται από το  (Πάρτε περιπτώσεις για το
(Πάρτε περιπτώσεις για το  ).
).Διαιρείται από το
 διότι ο αριθμός
διότι ο αριθμός  διαιρείται από το
διαιρείται από το  (Πάρτε περιπτώσεις για το
(Πάρτε περιπτώσεις για το  ). Διαιρείται από το
). Διαιρείται από το  διότι ο αριθμός
διότι ο αριθμός  διαιρείται από το
διαιρείται από το  (Πάρτε περιπτώσεις για το
(Πάρτε περιπτώσεις για το  ) και τέλος διαιρείται από το
) και τέλος διαιρείται από το  διότι ο αριθμός
διότι ο αριθμός  διαιρείται από το
διαιρείται από το  (Πάρτε περιπτώσεις για το
(Πάρτε περιπτώσεις για το  ).
).Άρα αποκλείεται ο ΜΚΔ να είναι μεγαλύτερος από το
 .
.Όμως
 άρα
άρα .
.Αλέξανδρος
Αλέξανδρος Συγκελάκης
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Για την 4:
Θέλουμε δηλαδή
δηλαδή  για κάθε
για κάθε  φυσικό.
φυσικό.
Οπότε η παραπάνω ισχύει για και αντίστοιχα παίρνουμε
και αντίστοιχα παίρνουμε

 και τέλος
και τέλος
 .
.
Από τις παίρνουμε
παίρνουμε

Από τις παίρνουμε:
παίρνουμε:

Από τις παίρνουμε:
παίρνουμε:

Άρα τελικά
abc=1 ή 2 ή 3 ή 6.
Αν τότε
τότε  και πράγματι
και πράγματι  για κάθε
για κάθε  φυσικό.
φυσικό.
Αν τότε
τότε  και
και  (και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) και πράγματι
(και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) και πράγματι  για κάθε
για κάθε  φυσικό.
φυσικό.
Αν τότε
τότε  και
και  (και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) όμως
(και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) όμως  για κάθε
για κάθε  φυσικό (π.χ. για
φυσικό (π.χ. για  ).
).
Αν τότε είτε
τότε είτε  και
και  (και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) όμως
(και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) όμως 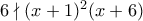 για κάθε
για κάθε  φυσικό (π.χ. για
φυσικό (π.χ. για  )
)
είτε (και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) και πράγματι
(και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) και πράγματι  (διότι το
(διότι το  διαιρεί το γινόμενο δύο διαδοχικών αριθμών και το
διαιρεί το γινόμενο δύο διαδοχικών αριθμών και το  διαιρεί το γινόμενο τριών διαδοχικών αριθμών άρα το
διαιρεί το γινόμενο τριών διαδοχικών αριθμών άρα το  διαιρεί το γινόμενο τριών διαδοχικών αριθμών).
διαιρεί το γινόμενο τριών διαδοχικών αριθμών).
Άρα οι λύσεις είναι και
και  και όλοι οι συνδυασμοί τους.
και όλοι οι συνδυασμοί τους.
Αλέξανδρος
Θέλουμε
 δηλαδή
δηλαδή  για κάθε
για κάθε  φυσικό.
φυσικό.Οπότε η παραπάνω ισχύει για
 και αντίστοιχα παίρνουμε
και αντίστοιχα παίρνουμε
 και τέλος
και τέλος  .
.Από τις
 παίρνουμε
παίρνουμε
Από τις
 παίρνουμε:
παίρνουμε:
Από τις
 παίρνουμε:
παίρνουμε:
Άρα τελικά
abc=1 ή 2 ή 3 ή 6.
Αν
 τότε
τότε  και πράγματι
και πράγματι  για κάθε
για κάθε  φυσικό.
φυσικό.Αν
 τότε
τότε  και
και  (και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) και πράγματι
(και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) και πράγματι  για κάθε
για κάθε  φυσικό.
φυσικό.Αν
 τότε
τότε  και
και  (και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) όμως
(και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) όμως  για κάθε
για κάθε  φυσικό (π.χ. για
φυσικό (π.χ. για  ).
).Αν
 τότε είτε
τότε είτε  και
και  (και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) όμως
(και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) όμως 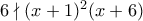 για κάθε
για κάθε  φυσικό (π.χ. για
φυσικό (π.χ. για  )
)είτε
 (και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) και πράγματι
(και όμοια όλοι οι υπόλοιποι συνδυασμοί λόγω συμμετρίας) και πράγματι  (διότι το
(διότι το  διαιρεί το γινόμενο δύο διαδοχικών αριθμών και το
διαιρεί το γινόμενο δύο διαδοχικών αριθμών και το  διαιρεί το γινόμενο τριών διαδοχικών αριθμών άρα το
διαιρεί το γινόμενο τριών διαδοχικών αριθμών άρα το  διαιρεί το γινόμενο τριών διαδοχικών αριθμών).
διαιρεί το γινόμενο τριών διαδοχικών αριθμών).Άρα οι λύσεις είναι
 και
και  και όλοι οι συνδυασμοί τους.
και όλοι οι συνδυασμοί τους.Αλέξανδρος
Αλέξανδρος Συγκελάκης
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Για την 5:
Ονομάζουμε .
.
Προφανώς για έχουμε
έχουμε  . Θα δείξουμε ότι αυτή είναι και η ελάχιστη τιμή που λαμβάνει η παράσταση
. Θα δείξουμε ότι αυτή είναι και η ελάχιστη τιμή που λαμβάνει η παράσταση  .
.
Το διαιρείται από το
διαιρείται από το  , άρα το
, άρα το  μπορεί να είναι κάποιος από τους
μπορεί να είναι κάποιος από τους 
Επίσης όταν το διαιρεθεί με το
διαιρεθεί με το  αφήνει υπόλοιπο
αφήνει υπόλοιπο  , άρα το
, άρα το  μπορεί να είναι
μπορεί να είναι  .
.
Από τα κοινά στοιχεία το μπορεί να είναι
μπορεί να είναι  .
.
Λήμμα (εύκολο): Ο αριθμός τελειώνει σε
τελειώνει σε  όταν το
όταν το  είναι περιττός και σε 2 ή 8 όταν το
είναι περιττός και σε 2 ή 8 όταν το  είναι άρτιος.
είναι άρτιος.
Το δεν μπορεί να είναι
δεν μπορεί να είναι  διότι η εξίσωση
διότι η εξίσωση  δεν μπορεί να υφίσταται για θετικούς φυσικούς
δεν μπορεί να υφίσταται για θετικούς φυσικούς  διότι (*) αφού το δεύτερο μέλος είναι τέλειο τετράγωνο άρα πρέπει να είναι και το πρώτο. Παίρνοντας όμως
διότι (*) αφού το δεύτερο μέλος είναι τέλειο τετράγωνο άρα πρέπει να είναι και το πρώτο. Παίρνοντας όμως  έχουμε
έχουμε  (και για άρτια και για περιττά
(και για άρτια και για περιττά  ). Όμως το
). Όμως το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  .
.
To δεν μπορεί να είναι
δεν μπορεί να είναι  αφού τότε οι εξισώσεις
αφού τότε οι εξισώσεις  και
και 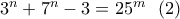 δεν μπορεί να υφίσταται για θετικούς φυσικούς
δεν μπορεί να υφίσταται για θετικούς φυσικούς  αφού (*):
αφού (*):
α) Για την : Για
: Για  περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε
περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε  και το δεύτερο είναι τέλειο τετράγωνο όμως κανένα τέλειο τετράγωνο δε λήγει σε
και το δεύτερο είναι τέλειο τετράγωνο όμως κανένα τέλειο τετράγωνο δε λήγει σε  . Για
. Για  άρτιο παίρνουμε στο πρώτο μέλος
άρτιο παίρνουμε στο πρώτο μέλος  και έτσι
και έτσι  και το
και το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο 
β) Για την : Για
: Για  περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε
περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε  και το δεύτερο είναι τέλειο τετράγωνο όμως κανένα τέλειο τετράγωνο δε λήγει σε
και το δεύτερο είναι τέλειο τετράγωνο όμως κανένα τέλειο τετράγωνο δε λήγει σε  . Για
. Για  άρτιο παίρνουμε στο πρώτο μέλος
άρτιο παίρνουμε στο πρώτο μέλος  και έτσι
και έτσι  και το
και το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο 
Το δεν μπορεί να είναι
δεν μπορεί να είναι  αφού τότε οι εξισώσεις
αφού τότε οι εξισώσεις  και
και  δεν μπορεί να υφίσταται για θετικούς φυσικούς
δεν μπορεί να υφίσταται για θετικούς φυσικούς  αφού (*):
αφού (*):
α) Για την :
:  και το 3 δεν είναι τετραγωνικό υπόλοιπο
και το 3 δεν είναι τετραγωνικό υπόλοιπο  .
.
β) Για την : Για
: Για  περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε
περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε  και το δεύτερο τελειώνει σε
και το δεύτερο τελειώνει σε  . Για
. Για  άρτιο το πρώτο μέλος (από το Λήμμα) τελειώνει σε
άρτιο το πρώτο μέλος (από το Λήμμα) τελειώνει σε  ή
ή  ενώ το δεύτερο τελειώνει σε 5.
ενώ το δεύτερο τελειώνει σε 5.
Άρα τελικά η ελάχιστη τιμή του είναι η
είναι η  για
για  .
.
Αλέξανδρος
EDIT: (*) Έκανα ένα γενικό ρεκτιφιέ στα παραπάνω σημεία σύμφωνα με τις σωστές υποδείξεις του Κυριάκου (userresu) και πρόσθεσα ένα χρήσιμο Λήμμα.
Ονομάζουμε
 .
.Προφανώς για
 έχουμε
έχουμε  . Θα δείξουμε ότι αυτή είναι και η ελάχιστη τιμή που λαμβάνει η παράσταση
. Θα δείξουμε ότι αυτή είναι και η ελάχιστη τιμή που λαμβάνει η παράσταση  .
.Το
 διαιρείται από το
διαιρείται από το  , άρα το
, άρα το  μπορεί να είναι κάποιος από τους
μπορεί να είναι κάποιος από τους 
Επίσης όταν το
 διαιρεθεί με το
διαιρεθεί με το  αφήνει υπόλοιπο
αφήνει υπόλοιπο  , άρα το
, άρα το  μπορεί να είναι
μπορεί να είναι  .
.Από τα κοινά στοιχεία το
 μπορεί να είναι
μπορεί να είναι  .
.Λήμμα (εύκολο): Ο αριθμός
 τελειώνει σε
τελειώνει σε  όταν το
όταν το  είναι περιττός και σε 2 ή 8 όταν το
είναι περιττός και σε 2 ή 8 όταν το  είναι άρτιος.
είναι άρτιος.Το
 δεν μπορεί να είναι
δεν μπορεί να είναι  διότι η εξίσωση
διότι η εξίσωση  δεν μπορεί να υφίσταται για θετικούς φυσικούς
δεν μπορεί να υφίσταται για θετικούς φυσικούς  διότι (*) αφού το δεύτερο μέλος είναι τέλειο τετράγωνο άρα πρέπει να είναι και το πρώτο. Παίρνοντας όμως
διότι (*) αφού το δεύτερο μέλος είναι τέλειο τετράγωνο άρα πρέπει να είναι και το πρώτο. Παίρνοντας όμως  έχουμε
έχουμε  (και για άρτια και για περιττά
(και για άρτια και για περιττά  ). Όμως το
). Όμως το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  .
.To
 δεν μπορεί να είναι
δεν μπορεί να είναι  αφού τότε οι εξισώσεις
αφού τότε οι εξισώσεις  και
και 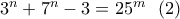 δεν μπορεί να υφίσταται για θετικούς φυσικούς
δεν μπορεί να υφίσταται για θετικούς φυσικούς  αφού (*):
αφού (*):α) Για την
 : Για
: Για  περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε
περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε  και το δεύτερο είναι τέλειο τετράγωνο όμως κανένα τέλειο τετράγωνο δε λήγει σε
και το δεύτερο είναι τέλειο τετράγωνο όμως κανένα τέλειο τετράγωνο δε λήγει σε  . Για
. Για  άρτιο παίρνουμε στο πρώτο μέλος
άρτιο παίρνουμε στο πρώτο μέλος  και έτσι
και έτσι  και το
και το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο 
β) Για την
 : Για
: Για  περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε
περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε  και το δεύτερο είναι τέλειο τετράγωνο όμως κανένα τέλειο τετράγωνο δε λήγει σε
και το δεύτερο είναι τέλειο τετράγωνο όμως κανένα τέλειο τετράγωνο δε λήγει σε  . Για
. Για  άρτιο παίρνουμε στο πρώτο μέλος
άρτιο παίρνουμε στο πρώτο μέλος  και έτσι
και έτσι  και το
και το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο 
Το
 δεν μπορεί να είναι
δεν μπορεί να είναι  αφού τότε οι εξισώσεις
αφού τότε οι εξισώσεις  και
και  δεν μπορεί να υφίσταται για θετικούς φυσικούς
δεν μπορεί να υφίσταται για θετικούς φυσικούς  αφού (*):
αφού (*):α) Για την
 :
:  και το 3 δεν είναι τετραγωνικό υπόλοιπο
και το 3 δεν είναι τετραγωνικό υπόλοιπο  .
.β) Για την
 : Για
: Για  περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε
περιττό (από το Λήμμα) το πρώτο μέλος τελειώνει σε  και το δεύτερο τελειώνει σε
και το δεύτερο τελειώνει σε  . Για
. Για  άρτιο το πρώτο μέλος (από το Λήμμα) τελειώνει σε
άρτιο το πρώτο μέλος (από το Λήμμα) τελειώνει σε  ή
ή  ενώ το δεύτερο τελειώνει σε 5.
ενώ το δεύτερο τελειώνει σε 5.Άρα τελικά η ελάχιστη τιμή του
 είναι η
είναι η  για
για  .
.Αλέξανδρος
EDIT: (*) Έκανα ένα γενικό ρεκτιφιέ στα παραπάνω σημεία σύμφωνα με τις σωστές υποδείξεις του Κυριάκου (userresu) και πρόσθεσα ένα χρήσιμο Λήμμα.
Αλέξανδρος Συγκελάκης
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Νομίζω πως αυτό ισχύει μόνο για περιττά n.cretanman έγραψε:Τοδεν μπορεί να είναι
διότι η εξίσωση
δεν μπορεί να υφίσταται για θετικούς φυσικούς
αφού το πρώτο μέλος τελειώνει σε
ενώ το δεύτερο σε
.
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Έχεις δίκιο! Αυτό διορθώνεται εύκολα όμως: το δεύτερο μέλος είναι τέλειο τετράγωνο άρα πρέπει να είναι και το πρώτο. Παίρνοντας
όμως έχουμε
έχουμε  (και για άρτια και για περιττά
(και για άρτια και για περιττά  ). Όμως το
). Όμως το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  και τελειώσαμε.
και τελειώσαμε.
Κάνω την απαραίτητη διόρθωση παραπάνω! Ευχαριστώ.
Αλέξανδρος
όμως
 έχουμε
έχουμε  (και για άρτια και για περιττά
(και για άρτια και για περιττά  ). Όμως το
). Όμως το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  και τελειώσαμε.
και τελειώσαμε.Κάνω την απαραίτητη διόρθωση παραπάνω! Ευχαριστώ.
Αλέξανδρος
Αλέξανδρος Συγκελάκης
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Για την 6:
Ας υποθέσουμε αντίθετα ότι ο αριθμός είναι τέλειο τετράγωνο. Κάνουμε τις πράξεις και παίρνουμε . Τότε για το δοσμένο αριθμό
. Τότε για το δοσμένο αριθμό  ισχύει:
ισχύει:
 . Όμως επειδή
. Όμως επειδή  άρα
άρα  οπότε εκτελώντας τη διαίρεση του
οπότε εκτελώντας τη διαίρεση του  με το
με το  παίρνουμε
παίρνουμε 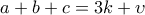 , με
, με  .
.
Τότε .
.
Για παίρνουμε
παίρνουμε  αντίστοιχα. Όμως κανένας από τους
αντίστοιχα. Όμως κανένας από τους  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  , άτοπο.
, άτοπο.
Αλέξανδρος
Ας υποθέσουμε αντίθετα ότι ο αριθμός είναι τέλειο τετράγωνο. Κάνουμε τις πράξεις και παίρνουμε
 . Τότε για το δοσμένο αριθμό
. Τότε για το δοσμένο αριθμό  ισχύει:
ισχύει: . Όμως επειδή
. Όμως επειδή  άρα
άρα  οπότε εκτελώντας τη διαίρεση του
οπότε εκτελώντας τη διαίρεση του  με το
με το  παίρνουμε
παίρνουμε 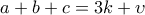 , με
, με  .
.Τότε
 .
. Για
 παίρνουμε
παίρνουμε  αντίστοιχα. Όμως κανένας από τους
αντίστοιχα. Όμως κανένας από τους  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  , άτοπο.
, άτοπο.Αλέξανδρος
Αλέξανδρος Συγκελάκης
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Φίλε cretanman, νομίζω πως χρησιμοποιείς το ίδιο συμπέρασμα ξανά στη λύση σου, στα εξής:
Κυριάκος.cretanman έγραψε:Toδεν μπορεί να είναι
αφού τότε οι εξισώσεις
και
δεν μπορεί να υφίσταται για θετικούς φυσικούς
αφού:
α) Για την: το πρώτο μέλος τελειώνει σε
και το δεύτερο είναι τέλειο τετράγωνο όμως κανένα τέλειο τετράγωνο δε λήγει σε
.
β) Για την: το πρώτο μέλος τελειώνει σε
και το δεύτερο είναι τέλειο τετράγωνο όμως κανένα τέλειο τετράγωνο δε λήγει σε
.
Τοδεν μπορεί να είναι
αφού τότε οι εξισώσεις
και
δεν μπορεί να υφίσταται για θετικούς φυσικούς
αφού:
α) Για την:
ενώ
.
β) Για την: το πρώτο μέλος τελειώνει σε
και το δεύτερο τελειώνει σε
.
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Κυριάκο έκανα ένα γενικό ρεκτιφιέ στην άσκηση! Σ' ευχαριστώ πολύ! Και να φανταστείς ότι την πρώην (λανθασμένη) δικαιολόγηση την έγραψα για συντομία και για να μην μπλέξω πολύ πολύ τα  χωρίς όμως να παρατηρήσω ότι είχα κάνει λάθος. Αν ξέμεινε κι άλλο λάθος τότε θα την σβήσω και θα την ξαναγράψω από την αρχή!
χωρίς όμως να παρατηρήσω ότι είχα κάνει λάθος. Αν ξέμεινε κι άλλο λάθος τότε θα την σβήσω και θα την ξαναγράψω από την αρχή! 
Αλέξανδρος
 χωρίς όμως να παρατηρήσω ότι είχα κάνει λάθος. Αν ξέμεινε κι άλλο λάθος τότε θα την σβήσω και θα την ξαναγράψω από την αρχή!
χωρίς όμως να παρατηρήσω ότι είχα κάνει λάθος. Αν ξέμεινε κι άλλο λάθος τότε θα την σβήσω και θα την ξαναγράψω από την αρχή! Αλέξανδρος
Αλέξανδρος Συγκελάκης
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Για την 3
Η δοσμένη παράσταση είναι ίση με , και για να είναι αυτό φυσικός, θα πρέπει
, και για να είναι αυτό φυσικός, θα πρέπει 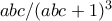 , και αφού
, και αφού  , για οποιαδήποτε
, για οποιαδήποτε  , θα πρέπει υποχρεωτικά
, θα πρέπει υποχρεωτικά  , δηλαδή
, δηλαδή  .
.
Η δοσμένη παράσταση είναι ίση με
 , και για να είναι αυτό φυσικός, θα πρέπει
, και για να είναι αυτό φυσικός, θα πρέπει 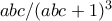 , και αφού
, και αφού  , για οποιαδήποτε
, για οποιαδήποτε  , θα πρέπει υποχρεωτικά
, θα πρέπει υποχρεωτικά  , δηλαδή
, δηλαδή  .
. Κερδίζουμε ό,τι τολμούμε!
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Μια και έπεσα στο παραπάνω θέμα, επαναφέρω για τις ασκήσεις 1 και 2 που παραμένουν άλυτες.
Αλέξανδρος
Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Αλέξανδρε και Μπάμπη,
Κάτι δεν πάει καλά με την Άσκηση 1. Μάλλον λείπουν υποθέσεις.
Ως έχει, μπορεί το σύνολο
 να έχει πλήθος στοιχείων οποιοδήποτε
να έχει πλήθος στοιχείων οποιοδήποτε  από
από  ως
ως  . Ας δούμε γιατί.
. Ας δούμε γιατί.Ορίζουμε το
 να έχει
να έχει  φορές τον αριθμό
φορές τον αριθμό  και μία φορά τον
και μία φορά τον  και
καιορίζουμε το
 να έχει
να έχει 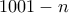 φορές τον αριθμό
φορές τον αριθμό  . (Βλέπε παρακάτω αν δεν μας αρέσει να επαναλαμβάνονται οι αριθμοί).
. (Βλέπε παρακάτω αν δεν μας αρέσει να επαναλαμβάνονται οι αριθμοί).Tώρα οι μέσοι όροι είναι, του μεν
 ο
ο  και του
και του  ο
ο  (όλοι οι αριθμοί είναι ίδιοι).
(όλοι οι αριθμοί είναι ίδιοι).Όταν φύγει ο
 από τον
από τον  , ο νέος μέσος όρος είναι
, ο νέος μέσος όρος είναι  (όλοι οι αριθμοί είναι ίδιοι), οπότε ο μ.ο. αυξήθηκε κατά
(όλοι οι αριθμοί είναι ίδιοι), οπότε ο μ.ο. αυξήθηκε κατά  .
. Επίσης, όταν ο
 προστεθεί στο
προστεθεί στο  , ο νέος μέσος όρος είναι
, ο νέος μέσος όρος είναι  , οπότε ο μ.ο. αυξήθηκε κατά
, οπότε ο μ.ο. αυξήθηκε κατά  .
. Δηλαδή ικανοποιούνται οι συνθήκες του προβλήματος, αλλά η απάντηση είναι πολλαπλή.
Προσθέτω ότι αν δεν μας αρέσει που οι αριθμοί σε κάθε σύνολο είναι σχεδόν όλοι ίδιοι, δεν έχουμε παρά να τους κουνήσουμε λιγάκι αλλά χωρίς να χαλάσουμε τον μέσο όρο.
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Για την 2:
Πρέπει ο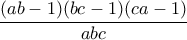 . Όμως, ισχύει
. Όμως, ισχύει  .
.
Οπότε παίρνοντας , θέλουμε
, θέλουμε  , ή αλλιώς, ο
, ή αλλιώς, ο  να είναι ακέραιος.
να είναι ακέραιος.
Προφανώς, , άρα
, άρα  . Είναι λοιπόν
. Είναι λοιπόν  .
.
Οπότε, .
.
Διακρίνουμε δύο περιπτώσεις.
Περίπτωση 1 : , επομένως
, επομένως  .
.
Αν , έστω
, έστω  , με
, με  . Αντικαθιστώντας, προκύπτει
. Αντικαθιστώντας, προκύπτει  , άτοπο.
, άτοπο.
Άρα, κάποιος εκ των είναι
είναι  . Έστω χωρίς βλάβη της γενικότητας
. Έστω χωρίς βλάβη της γενικότητας  . Τότε,
. Τότε,  , οπότε
, οπότε  ή
ή 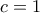 . Συνεπώς, προκύπτει η λύση
. Συνεπώς, προκύπτει η λύση  ,
,  , και οι μεταθέσεις αυτής.
, και οι μεταθέσεις αυτής.
Περίπτωση 2 : , επομένως
, επομένως  .
.
Αν κάποιος είναι έστω ο
έστω ο  , τότε προκύπτει
, τότε προκύπτει  , άτοπο.
, άτοπο.
Άρα, .
.
Αν τώρα , δηλαδή
, δηλαδή  , προκύπτει ξανά άτοπο.
, προκύπτει ξανά άτοπο.
Άρα, πρέπει ένας εκ των να είναι
να είναι  . Ας είναι ο
. Ας είναι ο  .
.
Θεωρούμε τώρα τη συνάρτηση (πρώτου βαθμού, ως προς
(πρώτου βαθμού, ως προς  ), με
), με  , άρα η
, άρα η  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.
Συνεπώς, .
.
Αν , τότε εύκολα
, τότε εύκολα  , και άρα δεν έχουμε καμία λύση.
, και άρα δεν έχουμε καμία λύση.
Αν , τότε
, τότε  και πλέον εύκολα προκύπτει
και πλέον εύκολα προκύπτει  , από όπου έχουμε τις λύσεις
, από όπου έχουμε τις λύσεις  και
και  .
.
Αν τότε
τότε  ή
ή  και διακρίνοντας περιπτώσεις και παραγοντοποιώντας κτλ προκύπτουν ξανά οι μεταθέσεις της
και διακρίνοντας περιπτώσεις και παραγοντοποιώντας κτλ προκύπτουν ξανά οι μεταθέσεις της  .
.
Τελικά, μόνες λύσεις οι ,
,  ,
,  και οι μεταθέσεις αυτών.
και οι μεταθέσεις αυτών.
Πρέπει ο
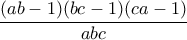 . Όμως, ισχύει
. Όμως, ισχύει  .
.Οπότε παίρνοντας
 , θέλουμε
, θέλουμε  , ή αλλιώς, ο
, ή αλλιώς, ο  να είναι ακέραιος.
να είναι ακέραιος.Προφανώς,
 , άρα
, άρα  . Είναι λοιπόν
. Είναι λοιπόν  .
.Οπότε,
 .
.Διακρίνουμε δύο περιπτώσεις.
Περίπτωση 1 :
 , επομένως
, επομένως  .
. Αν
 , έστω
, έστω  , με
, με  . Αντικαθιστώντας, προκύπτει
. Αντικαθιστώντας, προκύπτει  , άτοπο.
, άτοπο.Άρα, κάποιος εκ των
 είναι
είναι  . Έστω χωρίς βλάβη της γενικότητας
. Έστω χωρίς βλάβη της γενικότητας  . Τότε,
. Τότε,  , οπότε
, οπότε  ή
ή 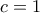 . Συνεπώς, προκύπτει η λύση
. Συνεπώς, προκύπτει η λύση  ,
,  , και οι μεταθέσεις αυτής.
, και οι μεταθέσεις αυτής.Περίπτωση 2 :
 , επομένως
, επομένως  .
.Αν κάποιος είναι
 έστω ο
έστω ο  , τότε προκύπτει
, τότε προκύπτει  , άτοπο.
, άτοπο.Άρα,
 .
.Αν τώρα
 , δηλαδή
, δηλαδή  , προκύπτει ξανά άτοπο.
, προκύπτει ξανά άτοπο.Άρα, πρέπει ένας εκ των
 να είναι
να είναι  . Ας είναι ο
. Ας είναι ο  .
.Θεωρούμε τώρα τη συνάρτηση
 (πρώτου βαθμού, ως προς
(πρώτου βαθμού, ως προς  ), με
), με  , άρα η
, άρα η  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.Συνεπώς,
 .
.Αν
 , τότε εύκολα
, τότε εύκολα  , και άρα δεν έχουμε καμία λύση.
, και άρα δεν έχουμε καμία λύση.Αν
 , τότε
, τότε  και πλέον εύκολα προκύπτει
και πλέον εύκολα προκύπτει  , από όπου έχουμε τις λύσεις
, από όπου έχουμε τις λύσεις  και
και  .
.Αν
 τότε
τότε  ή
ή  και διακρίνοντας περιπτώσεις και παραγοντοποιώντας κτλ προκύπτουν ξανά οι μεταθέσεις της
και διακρίνοντας περιπτώσεις και παραγοντοποιώντας κτλ προκύπτουν ξανά οι μεταθέσεις της  .
.Τελικά, μόνες λύσεις οι
 ,
,  ,
,  και οι μεταθέσεις αυτών.
και οι μεταθέσεις αυτών. Κερδίζουμε ό,τι τολμούμε!
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Για την 2, μία άλλη λύση (Συνεχίζω από την Περίπτωση 2)
Είναι .
.
Αν κάποιος είναι (έστω
(έστω  ) τότε
) τότε  , άτοπο.
, άτοπο.
Εξετάζουμε τώρα αν γίνεται κάποιο δύο να είναι ίσοι, π.χ. .
.
Τότε, , οπότε
, οπότε  , άτοπο.
, άτοπο.
Αν λοιπόν χωρίς βλάβη της γενικότητας , ισχύει
, ισχύει  .
.
Αν , τότε
, τότε  , οπότε
, οπότε  , άτοπο.
, άτοπο.
Οπότε, . Έστω
. Έστω  με
με  . Αντικαθιστούμε, και προκύπτει
. Αντικαθιστούμε, και προκύπτει  . Οπότε,
. Οπότε,  .
.
Τελικά λύση η και όλες οι μεταθέσεις.
και όλες οι μεταθέσεις.
Είναι
 .
. Αν κάποιος είναι
 (έστω
(έστω  ) τότε
) τότε  , άτοπο.
, άτοπο.Εξετάζουμε τώρα αν γίνεται κάποιο δύο να είναι ίσοι, π.χ.
 .
.Τότε,
 , οπότε
, οπότε  , άτοπο.
, άτοπο.Αν λοιπόν χωρίς βλάβη της γενικότητας
 , ισχύει
, ισχύει  .
.Αν
 , τότε
, τότε  , οπότε
, οπότε  , άτοπο.
, άτοπο.Οπότε,
 . Έστω
. Έστω  με
με  . Αντικαθιστούμε, και προκύπτει
. Αντικαθιστούμε, και προκύπτει  . Οπότε,
. Οπότε,  .
.Τελικά λύση η
 και όλες οι μεταθέσεις.
και όλες οι μεταθέσεις. Κερδίζουμε ό,τι τολμούμε!
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: ΑΣΚΗΣΕΙΣ ΓΙΑ ΑΡΧΙΜΗΔΗ Junior- BΑΛΚΑΝΙΑΔΑ ΝΕΩΝ,J-3.1
Πράγματι, τώρα που τη βλέπω, παρατηρώ ότι υπάρχει πρόβλημα! Ίσως ο Μπάμπης να έχει κρατήσει στο αρχείο του την πηγή της άσκησης και να βρει την σωστή εκφώνηση.Mihalis_Lambrou έγραψε: ↑Σάβ Δεκ 01, 2018 7:37 pmΑλέξανδρε και Μπάμπη,
Κάτι δεν πάει καλά με την Άσκηση 1. Μάλλον λείπουν υποθέσεις.
Αλέξανδρος
Αλέξανδρος Συγκελάκης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
