Αποδείξτε ότι σε κάθε τρίγωνο
 ισχύει
ισχύει 
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 ισχύει
ισχύει 
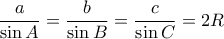 ,
,  ,
, 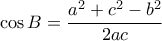 ,
,  ,
,  και
και  , έχουμε μετά από λίγες πράξεις την ισοδύναμη:
, έχουμε μετά από λίγες πράξεις την ισοδύναμη:



 που ισχύει.
που ισχύει. .
. το αριστερό μέλος της αποδεικτέας ανισότητας γράφεται
το αριστερό μέλος της αποδεικτέας ανισότητας γράφεται


![\displaystyle{\sum\limits_{cyc} {\frac{{{b^2} + {c^2}}}{a} = \frac{{{b^2}}}{a} + \frac{{{c^2}}}{a} + \frac{{{c^2}}}{b} + \frac{{{a^2}}}{b} + \frac{{{a^2}}}{c} + \frac{{{b^2}}}{c} \ge \frac{{{{\left[ {2\left( {a + b + c} \right)} \right]}^2}}}{{2\left( {a + b + c} \right)}} = 2\left( {a + b + c} \right)} ,} \displaystyle{\sum\limits_{cyc} {\frac{{{b^2} + {c^2}}}{a} = \frac{{{b^2}}}{a} + \frac{{{c^2}}}{a} + \frac{{{c^2}}}{b} + \frac{{{a^2}}}{b} + \frac{{{a^2}}}{c} + \frac{{{b^2}}}{c} \ge \frac{{{{\left[ {2\left( {a + b + c} \right)} \right]}^2}}}{{2\left( {a + b + c} \right)}} = 2\left( {a + b + c} \right)} ,}](/forum/ext/geomar/texintegr/latexrender/pictures/a91c47c4ac5332834cd1ed6d485d9cfa.png)
 είναι ισόπλευρο.
είναι ισόπλευρο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες