Δεύτερο μέρος: http://euclid.ucc.ie/pages/MATHENR/IrMO2012paper2.pdf
Θα προστεθούν σιγά σιγά και στα ελληνικά!
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 και
και 
 και
και  τέτοια ώστε
τέτοια ώστε 

 δεν ανήκει στο
δεν ανήκει στο 
 δεν ανήκει στο
δεν ανήκει στο  .
. βρίσκονται, με αυτή τη σειρά, στην περιφέρεια κύκλου
βρίσκονται, με αυτή τη σειρά, στην περιφέρεια κύκλου  Η
Η  είναι κάθετη στην
είναι κάθετη στην  και η
και η  στην
στην  Το σημείο
Το σημείο  βρίσκεται στην περιφέρεια του κύκλου, ανάμεσα στα
βρίσκεται στην περιφέρεια του κύκλου, ανάμεσα στα  και
και  Η
Η  , προεκτεινόμενη, τέμνει την προέκταση της
, προεκτεινόμενη, τέμνει την προέκταση της  στο
στο  και η
και η  , προεκτεινόμενη, τέμνει την προέκταση της
, προεκτεινόμενη, τέμνει την προέκταση της  στο
στο 
 εφάπτεται του περιγεγραμμένου κύκλου του
εφάπτεται του περιγεγραμμένου κύκλου του  και ότι η κοινή εφαπτομένη περνά από το κέντρο του
και ότι η κοινή εφαπτομένη περνά από το κέντρο του 
 με μη αρνητικούς ακέραιους συντελεστές και τέτοια ώστε
με μη αρνητικούς ακέραιους συντελεστές και τέτοια ώστε  και
και 

 Βρείτε άλλα δύο τέτοια τρίγωνα.
Βρείτε άλλα δύο τέτοια τρίγωνα. και
και  είναι θετικοί πραγματικοί αριθμοί, τότε
είναι θετικοί πραγματικοί αριθμοί, τότε 
 είναι η καλύτερη δυνατή.
είναι η καλύτερη δυνατή.  υπάρχουν θετικοί πραγματικοί αριθμοί
υπάρχουν θετικοί πραγματικοί αριθμοί  και
και  τέτοιοι ώστε
τέτοιοι ώστε 
 το άθροισμα των ψηφίων (στο δεκαδικό σύστημα) του αριθμού
το άθροισμα των ψηφίων (στο δεκαδικό σύστημα) του αριθμού  Για παράδειγμα,
Για παράδειγμα, 
 για τον οποίο
για τον οποίο 
 με
με  Η διχοτόμος της γωνίας
Η διχοτόμος της γωνίας  τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  στα σημεία
στα σημεία  και
και  Ο κύκλος κέντρου
Ο κύκλος κέντρου  και ακτίνας
και ακτίνας  τέμνει την ευθεία
τέμνει την ευθεία  σε δύο σημεία
σε δύο σημεία  και
και  Η ευθεία
Η ευθεία  τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  στα
στα  και
και 
 είναι το ορθόκεντρο του
είναι το ορθόκεντρο του 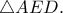

 ένας ακέραιος. Να δείξετε ότι ο αριθμός
ένας ακέραιος. Να δείξετε ότι ο αριθμός  διαιρείται με δύο τουλάχιστον διαφορετικούς πρώτους.
διαιρείται με δύο τουλάχιστον διαφορετικούς πρώτους. ένας θετικός ακέραιος. Σε κάθε γωνία ενός
ένας θετικός ακέραιος. Σε κάθε γωνία ενός  τετραγωνικού πίνακα κάθεται ένα ποντίκι όπως φαίνεται πιο κάτω για την περίπτωση
τετραγωνικού πίνακα κάθεται ένα ποντίκι όπως φαίνεται πιο κάτω για την περίπτωση  .
. για τις οποίες τα ποντίκια μπορούν να επιτύχουν αυτόν το στόχο.
για τις οποίες τα ποντίκια μπορούν να επιτύχουν αυτόν το στόχο.Μιας και έμεινε άλυτη ...
 έχει
έχει  ψηφία.
ψηφία. και
και  .
. .
. .
. , είναι
, είναι  (εύκολη απόδειξη με επαγωγή).
(εύκολη απόδειξη με επαγωγή). , δηλαδή ο
, δηλαδή ο  έχει το πολύ
έχει το πολύ  ψηφία.
ψηφία. , συνεπώς
, συνεπώς  , άρα ο
, άρα ο  (αν υπάρχει) θα είναι της μορφής
(αν υπάρχει) θα είναι της μορφής  με
με  .
. .
. .
.socrates έγραψε: ↑Δευ Δεκ 10, 2012 2:51 pm
7. Θεωρούμε τρίγωνομε
Η διχοτόμος της γωνίας
τέμνει τον περιγεγραμμένο κύκλο του
στα σημεία
και
Ο κύκλος κέντρου
και ακτίνας
τέμνει την ευθεία
σε δύο σημεία
και
Η ευθεία
τέμνει τον περιγεγραμμένο κύκλο του
στα
και
Να αποδείξετε ότι τοείναι το ορθόκεντρο του
Ευχαριστώ το Δημήτρη για τη μετάφραση του τελευταίου θέματος!
 τότε η διχοτόμος της
τότε η διχοτόμος της  τέμνει τον περιγεγραμμένο κύκλο του τριγώνου
τέμνει τον περιγεγραμμένο κύκλο του τριγώνου  στο
στο  kai
kai  . Η μεσοκάθετη της
. Η μεσοκάθετη της  τέμνει την
τέμνει την  μόνο σε ένα σημείο αφού οι ευθείες δεν ταυτίζονται άρα υπάρχει μόνο ένα σημείο της διχοτόμου που να ισαπέχει από τα
μόνο σε ένα σημείο αφού οι ευθείες δεν ταυτίζονται άρα υπάρχει μόνο ένα σημείο της διχοτόμου που να ισαπέχει από τα  οπότε
οπότε  . Όμως τώρα
. Όμως τώρα  εγγράψιμο αλλά το
εγγράψιμο αλλά το  δεν ανοίκει στον περιγεγραμμένο κύκλο του
δεν ανοίκει στον περιγεγραμμένο κύκλο του  οπότε καταλήγουμε σε άτοπο. Άρα
οπότε καταλήγουμε σε άτοπο. Άρα  και
και  (i) (Aφού η ΑD είναι και δοχοτόμος στο ισοσκελές).
(i) (Aφού η ΑD είναι και δοχοτόμος στο ισοσκελές).  δοχοτομεί
δοχοτομεί  αφού
αφού  από εγγράψιμο και από τον κύκλο τον δεύτερο της εκφώνησεις
από εγγράψιμο και από τον κύκλο τον δεύτερο της εκφώνησεις  . Θεωρούμε
. Θεωρούμε  και με τον ίδιο τρόπο όπως πριν καταλήγουμε σε άτοπο και μετά βγάζουμε το ίδιο συμπέρασμα δηλαδή
και με τον ίδιο τρόπο όπως πριν καταλήγουμε σε άτοπο και μετά βγάζουμε το ίδιο συμπέρασμα δηλαδή  (ii). Από (i),(ii)
(ii). Από (i),(ii)  ορθόκεντρο
ορθόκεντρο 
Έστωsocrates έγραψε: ↑Δευ Δεκ 10, 2012 2:51 pm
2. Τα σημείαβρίσκονται, με αυτή τη σειρά, στην περιφέρεια κύκλου
Η
είναι κάθετη στην
και η
στην
Το σημείο
βρίσκεται στην περιφέρεια του κύκλου, ανάμεσα στα
και
Η
, προεκτεινόμενη, τέμνει την προέκταση της
στο
και η
, προεκτεινόμενη, τέμνει την προέκταση της
στο
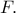
Να δείξετε ότι ο περιγεγραμμένος κύκλος του τριγώνουεφάπτεται του περιγεγραμμένου κύκλου του
και ότι η κοινή εφαπτομένη περνά από το κέντρο του

 το κέντρο του κύκλου
το κέντρο του κύκλου  .
. εφάπτεται στον κύκλο
εφάπτεται στον κύκλο  και στον
και στον  , τότε οι δύο κύκλοι εφάπτεται και η κοινή εφαπτόμενη περνά από το
, τότε οι δύο κύκλοι εφάπτεται και η κοινή εφαπτόμενη περνά από το  .
. η
η  εφάπτεται στον κύκλο
εφάπτεται στον κύκλο  .
. , και άρα η απόδειξη ολοκληρώθηκε.
, και άρα η απόδειξη ολοκληρώθηκε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες