Ακόμα καλύτερα, λύστε την παραπάνω εξίσωση.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Κυρ Ιαν 14, 2018 12:59 amΑΣΚΗΣΗ 601: Αν οι αριθμοίείναι θετικοί ακέραιοι και ισχύει ότι
, ...
Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Μάγκος Θάνος
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Καλημέρα Θάνο.matha έγραψε: ↑Κυρ Ιαν 14, 2018 10:11 amΑκόμα καλύτερα, λύστε την παραπάνω εξίσωση.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Κυρ Ιαν 14, 2018 12:59 amΑΣΚΗΣΗ 601: Αν οι αριθμοίείναι θετικοί ακέραιοι και ισχύει ότι
, ...
Την έθεσα έτσι, για να δούμε αν οι μαθητές (απευθύνεται σε Γ Γυμνασίου, αρχάριους) θα έκαναν αντικατάσταση και τα δύο ζεύγη τιμών στην ζητούμενη σχέση ή αν θα αρκούνταν μόνο στο ένα...
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
ΑΣΚΗΣΗ 602: Έστω 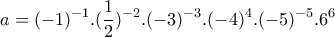
και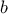 ακέραιος με
ακέραιος με  . Αν γνωρίζουμε ότι ο αριθμός
. Αν γνωρίζουμε ότι ο αριθμός  είναι ρητός, να βρεθεί
είναι ρητός, να βρεθεί
ο ακέραιος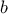 .
.
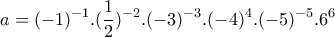
και
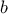 ακέραιος με
ακέραιος με  . Αν γνωρίζουμε ότι ο αριθμός
. Αν γνωρίζουμε ότι ο αριθμός  είναι ρητός, να βρεθεί
είναι ρητός, να βρεθεί ο ακέραιος
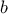 .
.-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Η λύση της άσκησης 564 είναι απλή.Mihalis_Lambrou έγραψε: ↑Δευ Ιούλ 27, 2015 1:26 pmΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 564: (Βαθμός δυσκολίας 4, με κλίμακα από το 1 μέχρι το 10). Να βρείτε ένα πολυώνυμομε ακεραίους συντελεστές,
τέτοιο ώστε να υπάρχουν ακέραιοι αριθμοί, ώστε οι αριθμοί
να είναι όλοι τους πρώτοι και διαφορετικοί
μεταξύ τους
Δεν θα γράψω λύση γιατί την ξέρω ήδη αλλά θέλω να κάνω ένα ιστορικό σχόλιο και να θέσω ένα συμπληρωματικό ερώτημα.
Ιστορικό σχόλιο: Ο Euler βρήκε ένα απίστευτο τέτοιο πολυώνυμο. Είναι μόνο δευτέρου βαθμού και όμως δίνει διαφορετικούς πρώτους γιαδιαδοχικές τιμές του
, τις
. Λίγο αργότερα ο Legendre το ξαναβρήκε (σε ισοδύναμη μορφή) ανεξάρτητα από τον Euler.
Συμπλήρωμα: Δείξτε ότι δεν υπάρχει μη σταθερό πολυώνυμομε ακεραίους συντελεστές, που να δίνει διαφορετικούς πρώτους για όλα τα
.
Φιλικά,
Μιχάλης
Αρκεί να πάρουμε το
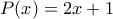
Μάλιστα παίρνουμε όλους τους πρώτους εκτός του
 .
.Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
matha έγραψε: ↑Δευ Αύγ 13, 2012 1:09 pmΑς είναιΜπάμπης Στεργίου έγραψε:Από τη βόρεια Εύβοια στέλνω την παρακάτω άσκηση στην ωραία πρωτοβουλία του Γιώργου
-----------------------
Άσκηση 8
Αν,
και οι όροι των κλασμάτων έχουν το ίδιο πλήθος ψηφίων, να αποδείξετε ότι
και
Τότε,
και
Επειδήαρκεί να αποδειχθεί ότι
δηλαδή ότι
Όμως, είναι
και

-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Μενέλαε, καλώς ήλθες στο φόρουμ.
Υπάρχει κάποιος λόγος που έστειλες το προηγούμενο μήνυμα, που είναι το ποστ άλλου πριν από χρόνια; Χάνω κάτι;
χρόνια; Χάνω κάτι;
Υπάρχει κάποιος λόγος που έστειλες το προηγούμενο μήνυμα, που είναι το ποστ άλλου πριν από
 χρόνια; Χάνω κάτι;
χρόνια; Χάνω κάτι;Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Είμαι σχετικά αρχάριος σε τέτοιου είδους ασκήσεις μη γνωρίζοντας τι είναι το LHS ....sokratis lyras έγραψε: ↑Παρ Αύγ 31, 2012 8:33 pmΚλεόβουλε μου φαίνεται πως το μοναδικό που χρειάζεται να γνωρίζεις για να λύσεις αυτήν την άσκηση είναι μόνο το τί είναι ένας ακέραιος αριθμός(που νομίζω ότι το γνωρίζεις).exdx έγραψε:Άσκηση 20
Να βρεθούν όλες οι τριάδες ακεραίων αριθμώνπου ικανοποιούν τη σχέση
Αρκεί να παρατηρήσουμε ότι :και αφού
τα πράγματα είναι απλά.
**Έκανα μια μικρή διόρθωση.Ευχαριστώ exdx
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Εκεί δεν έχεις άδικο. LHS= Left Hand Side = αριστερό μέλος. Προφανώς ο λύτης χρησιμοποίησε αυτή την αγγλική ορολογία
γιατί γράφει σε latex, οπότε η φράση "αριστερό μέλος" ελληνιστί είναι φασαρία να γραφεί.
Κάτι ακόμα. Είδες το προηγούμενο μήνυμά μου, λίγα ποστ πιο πάνω, που απευθύνεται σε σένα; Τι αιτιολογία δίνεις;
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Καλησπέρα ,Μπάμπης Στεργίου έγραψε: ↑Παρ Σεπ 21, 2012 10:48 amΑΣΚΗΣΗ 28
Αν οι φυσικοί αριθμοίείναι τέλειοι κύβοι, να αποδειχθεί ότι και οι φυσικοί αριθμοί
είναι τέλειοι κύβοι.
Μπάμπης
μπορούμε να το αποδείξουμε αντικαθιστώντας τις μεταβλητές με τέλειους κύβους ?
Ευχαριστώ
τελευταία επεξεργασία από Μενέλαος σε Δευ Ιαν 07, 2019 7:58 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δεν είναι απαραίτητοΜενέλαος έγραψε: ↑Δευ Ιαν 07, 2019 6:48 pmΚαλησπέρα ,Μπάμπης Στεργίου έγραψε: ↑Παρ Σεπ 21, 2012 10:48 amΑΣΚΗΣΗ 28
Αν οι φυσικοί αριθμοίείναι τέλειοι κύβοι, να αποδειχθεί ότι και οι φυσικοί αριθμοί
είναι τέλειοι κύβοι.
Μπάμπης
μπορούμε να το αποδείξουμε αντικαθιστώντας τις μεταβλητές με τέλεια τετράγωνα ?
Ευχαριστώ
Πάρε π.χ
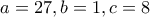
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Νομίζω ότι ρωτάει το εξής:ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Δευ Ιαν 07, 2019 6:54 pmΔεν είναι απαραίτητοΜενέλαος έγραψε: ↑Δευ Ιαν 07, 2019 6:48 pmΚαλησπέρα ,Μπάμπης Στεργίου έγραψε: ↑Παρ Σεπ 21, 2012 10:48 amΑΣΚΗΣΗ 28
Αν οι φυσικοί αριθμοίείναι τέλειοι κύβοι, να αποδειχθεί ότι και οι φυσικοί αριθμοί
είναι τέλειοι κύβοι.
Μπάμπης
μπορούμε να το αποδείξουμε αντικαθιστώντας τις μεταβλητές με τέλεια τετράγωνα ?
Ευχαριστώ
Πάρε π.χ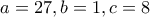
Αν οι φυσικοί αριθμοί
 είναι τέλεια τετράγωνα , να αποδειχθεί ότι και οι φυσικοί αριθμοί
είναι τέλεια τετράγωνα , να αποδειχθεί ότι και οι φυσικοί αριθμοί  είναι τέλεια τετράγωνα .
είναι τέλεια τετράγωνα .Η απάντηση είναι όχι .Για παράδειγμα
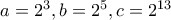
και φυσικά μπορούμε να φτιάξουμε άπειρα παραδείγματα
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Μενέλαε,Μενέλαος έγραψε: ↑Δευ Ιαν 07, 2019 6:48 pmΚαλησπέρα ,Μπάμπης Στεργίου έγραψε: ↑Παρ Σεπ 21, 2012 10:48 amΑΣΚΗΣΗ 28
Αν οι φυσικοί αριθμοίείναι τέλειοι κύβοι, να αποδειχθεί ότι και οι φυσικοί αριθμοί
είναι τέλειοι κύβοι.
Μπάμπης
μπορούμε να το αποδείξουμε αντικαθιστώντας τις μεταβλητές με τέλεια τετράγωνα ?
Ευχαριστώ
με τρώει η περιέργεια: Πες ότι αντικαθιστούμε τα
 τέλεια τετράγωνα,
τέλεια τετράγωνα, 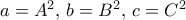 . Μετά τι; Έχεις κάποια λύση
. Μετά τι; Έχεις κάποια λύση από κει και πέρα; Θα χαιρόμουν να την δω.
Κάτι ακόμα. Μερικά ποστ πιο πάνω σε ρώτησα μία ερώτηση. Δεν την είδες ή ξέχασες να απαντήσεις;
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Με συγχωρείτε αλλά δεν πρόσεξα την επισήμανση σας. Την παλιά δημοσίευση την ξανά υπέβαλα κατά λάθος . Όσο αναφορά την τωρινή έκανα λάθος και αντί να γράψω τέλειους κύβους έγραψα τέλεια τετράγωναMihalis_Lambrou έγραψε: ↑Δευ Ιαν 07, 2019 7:43 pmΜενέλαε,Μενέλαος έγραψε: ↑Δευ Ιαν 07, 2019 6:48 pmΚαλησπέρα ,Μπάμπης Στεργίου έγραψε: ↑Παρ Σεπ 21, 2012 10:48 amΑΣΚΗΣΗ 28
Αν οι φυσικοί αριθμοίείναι τέλειοι κύβοι, να αποδειχθεί ότι και οι φυσικοί αριθμοί
είναι τέλειοι κύβοι.
Μπάμπης
μπορούμε να το αποδείξουμε αντικαθιστώντας τις μεταβλητές με τέλεια τετράγωνα ?
Ευχαριστώ
με τρώει η περιέργεια: Πες ότι αντικαθιστούμε τατέλεια τετράγωνα,
. Μετά τι; Έχεις κάποια λύση
από κει και πέρα; Θα χαιρόμουν να την δω.
Κάτι ακόμα. Μερικά ποστ πιο πάνω σε ρώτησα μία ερώτηση. Δεν την είδες ή ξέχασες να απαντήσεις;
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Καλή χρονιά Μενέλαε. Είναι φυσικό, για την ηλικία που έχεις να έχεις τέτοιου είδους απορίες. Και μόνο που θέλεις να ασχοληθείς με τέτοια θέματα, σου αξίζουν έπαινοι. Τώρα για αυτό που ρωτάς, όχι δεν μπορούμε να αντικαταστήσουμε ταΜενέλαος έγραψε: ↑Δευ Ιαν 07, 2019 8:02 pmΜε συγχωρείτε αλλά δεν πρόσεξα την επισήμανση σας. Την παλιά δημοσίευση την ξανά υπέβαλα κατά λάθος . Όσο αναφορά την τωρινή έκανα λάθος και αντί να γράψω τέλειους κύβους έγραψα τέλεια τετράγωναMihalis_Lambrou έγραψε: ↑Δευ Ιαν 07, 2019 7:43 pmΜενέλαε,Μενέλαος έγραψε: ↑Δευ Ιαν 07, 2019 6:48 pmΚαλησπέρα ,Μπάμπης Στεργίου έγραψε: ↑Παρ Σεπ 21, 2012 10:48 amΑΣΚΗΣΗ 28
Αν οι φυσικοί αριθμοίείναι τέλειοι κύβοι, να αποδειχθεί ότι και οι φυσικοί αριθμοί
είναι τέλειοι κύβοι.
Μπάμπης
μπορούμε να το αποδείξουμε αντικαθιστώντας τις μεταβλητές με τέλεια τετράγωνα ?
Ευχαριστώ
με τρώει η περιέργεια: Πες ότι αντικαθιστούμε τατέλεια τετράγωνα,
. Μετά τι; Έχεις κάποια λύση
από κει και πέρα; Θα χαιρόμουν να την δω.
Κάτι ακόμα. Μερικά ποστ πιο πάνω σε ρώτησα μία ερώτηση. Δεν την είδες ή ξέχασες να απαντήσεις;
 με
με  , αφού αυτό ακριβώς μας ζητάει η άσκηση. Δηλαδή, αν μας ζητάνε να δείξουμε κάτι, δεν μπορούμε να το θεωρήσουμε ως δεδομένο. Θα μπορούσες όμως να ισχυρισθείς ότι ένας τουλάχιστον από τους
, αφού αυτό ακριβώς μας ζητάει η άσκηση. Δηλαδή, αν μας ζητάνε να δείξουμε κάτι, δεν μπορούμε να το θεωρήσουμε ως δεδομένο. Θα μπορούσες όμως να ισχυρισθείς ότι ένας τουλάχιστον από τους  δεν είναι τέλειος κύβος και μετά με κατάλληλους συλλογισμούς να δείξεις ότι αυτό έρχεται σε αντίθεση με την υπόθεση , οπότε τότε θα είχες δείξει το ζητούμενο. Η μέθοδος αυτή λέγεται "εις άτοπον απαγωγή" και θα την συναντήσεις συχνά στις επόμενες τάξεις.
δεν είναι τέλειος κύβος και μετά με κατάλληλους συλλογισμούς να δείξεις ότι αυτό έρχεται σε αντίθεση με την υπόθεση , οπότε τότε θα είχες δείξει το ζητούμενο. Η μέθοδος αυτή λέγεται "εις άτοπον απαγωγή" και θα την συναντήσεις συχνά στις επόμενες τάξεις.- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Μία λύση για αυτήν (αν δεν έχει ήδη λυθεί):Μπάμπης Στεργίου έγραψε: ↑Παρ Σεπ 21, 2012 10:48 amΑΣΚΗΣΗ 28
Αν οι φυσικοί αριθμοίείναι τέλειοι κύβοι, να αποδειχθεί ότι και οι φυσικοί αριθμοί
είναι τέλειοι κύβοι.
Μπάμπης
Θα δείξω πρώτα το εξής Λήμμα:
Λήμμα
Αν
 και ισχύει
και ισχύει  , τότε
, τότε  και
και  για κάποιο φυσικό αριθμό
για κάποιο φυσικό αριθμό 
Απόδειξη
Έστω
 , οπότε υπάρχουν
, οπότε υπάρχουν  ώστε
ώστε  και
και  .
.Τότε,
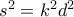 και
και 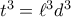 , οπότε
, οπότε  (1).
(1).Η (1) δίνει
 , και αφού
, και αφού  , πρέπει αναγκαστικά
, πρέπει αναγκαστικά  .
.Επομένως,
 και
και  ,
,  , οπότε το Λήμμα αποδείχτηκε.
, οπότε το Λήμμα αποδείχτηκε.Πάμε στην λύση της άσκησης τώρα.
Έστω
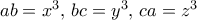 με
με  .
.Τότε, πολλαπλασιάζοντας τις παραπάνω κατά μέλη προκύπτει
 και από το Λήμμα, υπάρχει φυσικός
και από το Λήμμα, υπάρχει φυσικός  ώστε
ώστε  και
και  .
.Τότε όμως,
 , συνεπώς ο
, συνεπώς ο  είναι κύβος ρητού αριθμού, και αφού
είναι κύβος ρητού αριθμού, και αφού  , πρέπει να είναι κύβος φυσικού.
, πρέπει να είναι κύβος φυσικού.Όμοια, δείχνουμε ότι και οι
 είναι κύβοι φυσικών, και η απόδειξη ολοκληρώθηκε.
είναι κύβοι φυσικών, και η απόδειξη ολοκληρώθηκε. Κερδίζουμε ό,τι τολμούμε!
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Ας το δούμε και αλλιώς, χάριν πολυφωνίας.Ορέστης Λιγνός έγραψε: ↑Δευ Ιαν 07, 2019 11:53 pmΘα δείξω πρώτα το εξής Λήμμα:
Λήμμα
Ανκαι ισχύει
, τότε
και
για κάποιο φυσικό αριθμό
Από την
 εύκολα βλέπουμε ότι κάθε πρώτος παράγοντας του
εύκολα βλέπουμε ότι κάθε πρώτος παράγοντας του  είναι και του
είναι και του  , και αντίστροφα. Άρα για κάποιους πρώτους
, και αντίστροφα. Άρα για κάποιους πρώτους  είναι
είναι  , οπότε
, οπότε 
Από την μοναδικότητα της ανάλυσης σε πρώτους είναι
 για
για  . Άρα
. Άρα 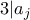 , όποτε μπορούμε να γράψουμε
, όποτε μπορούμε να γράψουμε 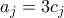 . Έχουμε τότε
. Έχουμε τότε 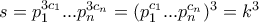 , όπως θέλαμε. Όμοια για τo
, όπως θέλαμε. Όμοια για τo  ή, αλλιώς, είναι
ή, αλλιώς, είναι  , άρα
, άρα  .
.-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Αν δεν έκανα κάποιο λάθος, μπορούμε να αποδείξουμε την γενίκευση της άσκησης αυτής, που είναι η εξής:Μπάμπης Στεργίου έγραψε: ↑Παρ Σεπ 21, 2012 10:48 amΑΣΚΗΣΗ 28
Αν οι φυσικοί αριθμοίείναι τέλειοι κύβοι, να αποδειχθεί ότι και οι φυσικοί αριθμοί
είναι τέλειοι κύβοι.
Μπάμπης
Αν
 είναι φυσικοί αριθμοί και αν
είναι φυσικοί αριθμοί και αν  , όπου ο
, όπου ο  είναι περιττός φυσικός αριθμός, τότε
είναι περιττός φυσικός αριθμός, τότε θα πρέπει :

-
Prødigy
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Το άθροισμα  διαφορετικών ανά δύο μετάξυ τους θετικών ακεραίων είναι ίσο με
διαφορετικών ανά δύο μετάξυ τους θετικών ακεραίων είναι ίσο με  .Να αποδειχθεί ότι το γινόμενο αυτών των αριθμών διαιρείται με τον
.Να αποδειχθεί ότι το γινόμενο αυτών των αριθμών διαιρείται με τον  .
.
Επίπεδο: Ευκλείδης Γ' Γυμνασίου
 διαφορετικών ανά δύο μετάξυ τους θετικών ακεραίων είναι ίσο με
διαφορετικών ανά δύο μετάξυ τους θετικών ακεραίων είναι ίσο με  .Να αποδειχθεί ότι το γινόμενο αυτών των αριθμών διαιρείται με τον
.Να αποδειχθεί ότι το γινόμενο αυτών των αριθμών διαιρείται με τον  .
.Επίπεδο: Ευκλείδης Γ' Γυμνασίου
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Αν
 οι αριθμοί, πρέπει
οι αριθμοί, πρέπει  .
.Είναι,
 (έχουμε επίσης ότι οι
(έχουμε επίσης ότι οι  είναι ανά δύο διαφορετικοί.
είναι ανά δύο διαφορετικοί.Οπότε,
 , οπότε
, οπότε  .
.Με την ίδια μέθοδο (τώρα, χρησιμοποιούμε τις
 ) προκύπτει
) προκύπτει  , και μετά
, και μετά  .
.Αν
 προκύπτουν
προκύπτουν  οπότε
οπότε  , αριθμός προφανώς διαιρετός από το
, αριθμός προφανώς διαιρετός από το  .
.Αν
 , τότε
, τότε 
 , άτοπο.
, άτοπο.Σε κάθε περίπτωση λοιπόν, το ζητούμενο δείχτηκε.
Κερδίζουμε ό,τι τολμούμε!
- ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
- Δημοσιεύσεις: 921
- Εγγραφή: Πέμ Νοέμ 22, 2018 9:43 pm
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Έστω
 οι αριθμοί.
οι αριθμοί.Είναι

Παρατηρούμε ότι αν κάποιος από αυτούς είναι
 τότε το ελάχιστο άθροισμά τους είναι
τότε το ελάχιστο άθροισμά τους είναι  .Άρα
.Άρα 
Είναι
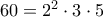
Αν κάποιος από αυτούς είναι
 τότε έχουμε αναγκαστικά
τότε έχουμε αναγκαστικά 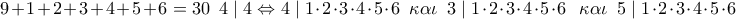
Άν
 υπάρχουν αναγκαστικά
υπάρχουν αναγκαστικά  ώστε
ώστε
Άρα αποδείχθηκε το ζητούμενο(Η περίπτωση να μην υπάρχει ο
 ανάμεσα στους
ανάμεσα στους  αποκλείτεται γιατί τότε δεν έχουμε άθροισμα
αποκλείτεται γιατί τότε δεν έχουμε άθροισμα 
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες








