Καλημέρα Mathematica, Καλημερα Κύριε Δημήτρη!!! Χαθήκαμε (ή μάλλον χάθηκα) για αρκετό καιρό...Σε περιοδο εξεταστικής είμαστε οπότε είπα για διάλλειμα να θυμηθώ τα παλιά


Στα δικά μας τώρα...
Αν και δεν μου άρεσε τόσο πολύ ο τρόπος (λίγο "μπακαλίστικος") θα περιγράψω το σκεπτικό αναλυτικά
Θέλουμε λόγω δεδομένων το

άρα

Το

όμως είναι θετικός ακέραιος και μπορούμε να συμπεράνουμε ότι η τετραγωνική ρίζα του

είναι ανάμεσα στο 4 και στο 5.
Συνεπώς οι δυνατές τιμές που μπορεί να πάρει το

είναι οι :

Στην εξίσωση του δεδομένου βάζοντας τις τιμές του

βρίσκω τις τιμές του

Για

Παρατηρώ ότι δεν υπάρχει θετικός ακέραιος

που να ικανοποιεί το δεδομένο
Για

Κάνοντας τις πράξεις βρίσκουμε οτι

και μάλιστα αυτό το ζευγάρι επαληθεύει το ζητούμενο (το

λύνοντας την ανίσωση από την ρίζα βρίσκουμε ότι πρέπει να είναι μεγαλύτερο ή ίσο του

άρα η τιμή είναι δεκτή.
Το

απορρίπτεται για τους ίδιους λόγους με το

Και τέλος το

και

επαληθεύει το πρόβλημα μας.
Ουσιαστικά το σκεπτικό είναι ότι θα βρώ όλα τα

και

που ικανοποιούν το δεδομένο και θα δείξω οτι ικανοποιούν και το ζητούμενο.
Ελπίζω λόγω και της περίεργης ώρας να μην έχω κάνει κάποια παρανόηση..
Κλείνοντας θέλω λίγο καθυστερημένα να ευχαριστήσω όλα τα μέλη του mathematica που στα "δυσκολα" χρόνια του λυκείου με βοήθησαν όχι μόνο για τις διαφορετικές ασκήσεις ή λύσεις που είδα ή τις απορίες που μου έλυσαν αλλά πιο πολύ επειδή με εκαναν να αγαπήσω ακόμα περισσοτερο τα μαθηματικα!
Καλό ξημέρωμα
Φιλικά
Μιχάλης

, να βρεθεί ο μη αρνητικός ακέραιος αριθμός
 η παράσταση.Είναι:
η παράσταση.Είναι: (Καθώς
(Καθώς  περιττός(άρα και το τετράγωνό του είναι περιττός) και ποτέ πολ. του
περιττός(άρα και το τετράγωνό του είναι περιττός) και ποτέ πολ. του  )
) (Αν
(Αν  , ισχύει πάντα η πρώτη περίπτωση. Αν
, ισχύει πάντα η πρώτη περίπτωση. Αν 

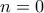 ισχύει η δεύτερη περίπτωση)
ισχύει η δεύτερη περίπτωση)
 . Παίρνουμε την δεύτερη περίπτωση που επιτυγχάνεται όταν
. Παίρνουμε την δεύτερη περίπτωση που επιτυγχάνεται όταν 



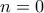 .
.

 είναι
είναι  , να βρεθούν οι αριθμοί
, να βρεθούν οι αριθμοί 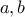
 και
και  έπεται ότι
έπεται ότι  , με
, με  . Επιπλέον, αφού το κλάσμα που δίνεται πάρνει και φυσικές τιμές έπεται ότι
. Επιπλέον, αφού το κλάσμα που δίνεται πάρνει και φυσικές τιμές έπεται ότι 




 Ευκολα τώρα βλέπουμε πως (αφού
Ευκολα τώρα βλέπουμε πως (αφού  φυσικοί και
φυσικοί και  )
) ,
,  . Όμως για να ισχύει η
. Όμως για να ισχύει η  . Αντικαθιστούμε στην άλλη και παίρνουμε
. Αντικαθιστούμε στην άλλη και παίρνουμε  , που (καθώς
, που (καθώς  φυσικός και
φυσικός και ) η ισότητα ισχύει μόνο αν
) η ισότητα ισχύει μόνο αν  , διαφορετικά η
, διαφορετικά η  , που ισχύει.
, που ισχύει. , που είναι φυσικός μόνο αν
, που είναι φυσικός μόνο αν  . Έτσι το ζεύγος
. Έτσι το ζεύγος  είναι και το μοναδικό.
είναι και το μοναδικό. και έστω
και έστω  το ύψος του. Ο κύκλος
το ύψος του. Ο κύκλος  τέμνει την
τέμνει την  στο σημείο
στο σημείο  . Αν η ευθεία
. Αν η ευθεία  τέμνει την βάση
τέμνει την βάση  στο
στο  ,
, και
και  είναι όμοια
είναι όμοια , να βρεθεί ο λόγος
, να βρεθεί ο λόγος 
 κέντρο του κύκλου,
κέντρο του κύκλου,  και
και  και ακόμη
και ακόμη  (από το ισοσκελές
(από το ισοσκελές  ).
). έχουν δύο ίσες γωνίες, και άρα είναι όμοια.
έχουν δύο ίσες γωνίες, και άρα είναι όμοια. .
. , όπου κάθε γράμμα αντιστοιχεί σε διαφορετικό ψηφίο, κανένα ψηφίο δεν μπορεί να είναι το
, όπου κάθε γράμμα αντιστοιχεί σε διαφορετικό ψηφίο, κανένα ψηφίο δεν μπορεί να είναι το  και κανένας αριθμός δεν ξεκινάει με το
και κανένας αριθμός δεν ξεκινάει με το  . Να βρείτε την ελάχιστη δυνατή τιμή του
. Να βρείτε την ελάχιστη δυνατή τιμή του  .
.
 είναι το 108. Καταρχάς, το
είναι το 108. Καταρχάς, το  , καθώς
, καθώς  . Έστω πως υπάρχει ένας
. Έστω πως υπάρχει ένας  και ότι
και ότι 

 , αλλά επειδή έχουμε ήδη χρησιμοποιήσει τα ψηφία 1 και 0, θα ισχύει ότι
, αλλά επειδή έχουμε ήδη χρησιμοποιήσει τα ψηφία 1 και 0, θα ισχύει ότι  ή
ή  . Όμως η λύση
. Όμως η λύση  απορρίπτεται, επειδή θα έπρεπε
απορρίπτεται, επειδή θα έπρεπε 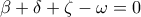 , που είναι αδύνατον αν χρησιμοποιήσουμε τα υπόλοιπα ψηφία 4, 6, 7, 8.
, που είναι αδύνατον αν χρησιμοποιήσουμε τα υπόλοιπα ψηφία 4, 6, 7, 8.  . Όμως επειδή πρέπει να χρησιμοποιήσουμε τα υπόλοιπα ψηφία 5,6,7 και 8, προκύπτει ότι
. Όμως επειδή πρέπει να χρησιμοποιήσουμε τα υπόλοιπα ψηφία 5,6,7 και 8, προκύπτει ότι  και
και  , άρα
, άρα  που ταυτίζεται με την αρχική μας λύση.
που ταυτίζεται με την αρχική μας λύση.  Να βρείτε όλες τις τριάδες θετικών ακεραίων
Να βρείτε όλες τις τριάδες θετικών ακεραίων  που ικανοποιούν το σύστημα των εξισώσεων
που ικανοποιούν το σύστημα των εξισώσεων 
 .
. .
. .
. .
. .
. .
.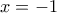 ,
,  .
. , και εύκολα έχουμε τις λύσεις
, και εύκολα έχουμε τις λύσεις  .
. και πιο μικροί
και πιο μικροί 



 , άτοπο. Συνεπώς, κανένας αριθμός δεν τηρεί τις προϋποθέσεις και άρα η απάντηση είναι
, άτοπο. Συνεπώς, κανένας αριθμός δεν τηρεί τις προϋποθέσεις και άρα η απάντηση είναι 

 έχουμε:
έχουμε:

 μπορεί να πάρει
μπορεί να πάρει  διαφορετικές τιμές.
διαφορετικές τιμές. , για τον οποίο ισχύει ότι
, για τον οποίο ισχύει ότι  και
και  .
. και βρίσκουμε έναν νέο αριθμό. Να αποδείξετε ότι αν από τον νέο αυτό αριθμό
και βρίσκουμε έναν νέο αριθμό. Να αποδείξετε ότι αν από τον νέο αυτό αριθμό .
. . Τώρα επειδή είναι
. Τώρα επειδή είναι  , έστω
, έστω  όπου
όπου  . Είναι λοιπόν,
. Είναι λοιπόν,  , και αφού
, και αφού  , έπεται πως ο αριθμός που προκύπτει (έστω
, έπεται πως ο αριθμός που προκύπτει (έστω  , στο δεκάδων
, στο δεκάδων  και στο μονάδων
και στο μονάδων  . Ο αριθμός που προκύπτει αν αλλάξουμε την σειρά των ψηφίων του
. Ο αριθμός που προκύπτει αν αλλάξουμε την σειρά των ψηφίων του  ) είναι
) είναι  . Τώρα κάνουμε την αφαίρεση
. Τώρα κάνουμε την αφαίρεση  και το ζητούμενο είναι άμεσο.
και το ζητούμενο είναι άμεσο. είναι μηδέν, τότε από τη σχέση
είναι μηδέν, τότε από τη σχέση  προκύπτει ότι το άθροισμα των άλλων δύο είναι μηδέν, οπότε τελικά είναι
προκύπτει ότι το άθροισμα των άλλων δύο είναι μηδέν, οπότε τελικά είναι  (αφού οι
(αφού οι 
![x+y+z \geq 3\sqrt[3]{xyz} \Leftrightarrow (xyz)^3 \geq 27(xyz) \Leftrightarrow (xyz)^2 \geq 27 \Leftrightarrow xyz \geq 3 \sqrt{3} x+y+z \geq 3\sqrt[3]{xyz} \Leftrightarrow (xyz)^3 \geq 27(xyz) \Leftrightarrow (xyz)^2 \geq 27 \Leftrightarrow xyz \geq 3 \sqrt{3}](/forum/ext/geomar/texintegr/latexrender/pictures/9fb9974e927225fa9be63e5cfa48472a.png) και οι
και οι 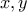 είναι θετικοί ακέραιοι και ισχύει ότι
είναι θετικοί ακέραιοι και ισχύει ότι  , τότε να αποδείξετε ότι
, τότε να αποδείξετε ότι 
 άρα
άρα 
 όμως είναι θετικός ακέραιος και μπορούμε να συμπεράνουμε ότι η τετραγωνική ρίζα του
όμως είναι θετικός ακέραιος και μπορούμε να συμπεράνουμε ότι η τετραγωνική ρίζα του  είναι ανάμεσα στο 4 και στο 5.
είναι ανάμεσα στο 4 και στο 5.
 Παρατηρώ ότι δεν υπάρχει θετικός ακέραιος
Παρατηρώ ότι δεν υπάρχει θετικός ακέραιος  Κάνοντας τις πράξεις βρίσκουμε οτι
Κάνοντας τις πράξεις βρίσκουμε οτι  και μάλιστα αυτό το ζευγάρι επαληθεύει το ζητούμενο (το
και μάλιστα αυτό το ζευγάρι επαληθεύει το ζητούμενο (το  άρα η τιμή είναι δεκτή.
άρα η τιμή είναι δεκτή. απορρίπτεται για τους ίδιους λόγους με το
απορρίπτεται για τους ίδιους λόγους με το  και
και  επαληθεύει το πρόβλημα μας.
επαληθεύει το πρόβλημα μας. που ικανοποιούν το δεδομένο και θα δείξω οτι ικανοποιούν και το ζητούμενο.
που ικανοποιούν το δεδομένο και θα δείξω οτι ικανοποιούν και το ζητούμενο.