Σελίδα 87 από 92
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Τετ Οκτ 14, 2015 1:42 am
από socrates
ΑΣΚΗΣΗ 580
Να δείξετε ότι για κάθε ακέραιο

, ο αριθμός

δε διαιρείται με το

.
socrates έγραψε:ΑΣΚΗΣΗ 576
Σε ένα τουρνουά συμμετείχαν

ομάδες. Κάθε ομάδα έπαιξε με κάθε άλλη ακριβώς μία φορά. Σε κάθε αγώνα, η νικήτρια ομάδα κέρδιζε

βαθμούς, η ηττημένη

βαθμούς ενώ σε περίπτωση ισοπαλίας οι δύο ομάδες κέρδιζαν από

βαθμό. Στο τέλος του τουρνουά, διαπιστώθηκε ότι το άθροισμα των βαθμών που κέρδισαν όλες οι ομάδες ήταν

Να δείξετε ότι υπάρχουν τέσσερις ομάδες, καθεμία από τις οποίες έφερε μία, τουλάχιστον, φορά ισοπαλία.
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Τετ Οκτ 14, 2015 9:55 am
από ealexiou
socrates έγραψε:ΑΣΚΗΣΗ 576
Σε ένα τουρνουά συμμετείχαν

ομάδες. Κάθε ομάδα έπαιξε με κάθε άλλη ακριβώς μία φορά. Σε κάθε αγώνα, η νικήτρια ομάδα κέρδιζε

βαθμούς, η ηττημένη

βαθμούς ενώ σε περίπτωση ισοπαλίας οι δύο ομάδες κέρδιζαν από

βαθμό. Στο τέλος του τουρνουά, διαπιστώθηκε ότι το άθροισμα των βαθμών που κέρδισαν όλες οι ομάδες ήταν

Να δείξετε ότι υπάρχουν τέσσερις ομάδες, καθεμία από τις οποίες έφερε μία, τουλάχιστον, φορά ισοπαλία.
Οι

ομάδες έπαιξαν

αγώνες.
Αν

οι αγώνες με νικητή και ηττημένο και

οι αγώνες με ισοπαλία τότε

και επειδή

,

. Συνεπώς τέσσερις ομάδες καθεμία από τις οποίες έφερε μία, τουλάχιστον, φορά ισοπαλία.
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Παρ Οκτ 30, 2015 9:49 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
ΑΣΚΗΣΗ 581 (Βαθμός δυσκολίας 2, με κλίμακα από το 1 μέχρι το 10): Αν

, με

, να αποδείξετε ότι:

Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Σάβ Οκτ 31, 2015 3:10 pm
από kostas232
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 581 (Βαθμός δυσκολίας 2, με κλίμακα από το 1 μέχρι το 10): Αν

, με

, να αποδείξετε ότι:

Επειδή οι

είναι θετικοί οι ρίζες, καθώς και τα κλάσματα, ορίζονται.
Πολλαπλασιάζοντας το πρώτο κλάσμα με

, το δεύτερο με

και το τρίτο με

, η ισότητα
που θέλουμε να αποδείξουμε γίνεται η:

Πολλαπλασιάζουμε το πρώτο κλάσμα με

και το τρίτο με

οπότε η (1) γίνεται

, που αληθεύει.
Κωνσταντίνος Τερζής
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Σάβ Οκτ 31, 2015 7:50 pm
από Παύλος Μαραγκουδάκης
socrates έγραψε:ΑΣΚΗΣΗ 580
Να δείξετε ότι για κάθε ακέραιο

, ο αριθμός

δε διαιρείται με το

.
Αν ο

δεν είναι πολλαπλάσιο του

τότε ο

δεν είναι πολλαπλάσιο του

Άρα και ο

δεν είναι πολλαπλάσιο του

, πόσο μάλλον του

Μένει να δούμε τι γίνεται όταν

όπου

ακέραιος. Τότε

Το γινόμενο

είναι πάντα πολλαπλάσιο του

ως γινόμενο τριών διαδοχικών ακεραίων (ένας από τους

είναι πολλαπλάσιο του 3).
Άρα ο αριθμός

είναι πολλαπλάσιο του 81 ενώ ο

διαιρούμενος με 81 αφήνει υπόλοιπο 27.
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Κυρ Νοέμ 01, 2015 7:09 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
ΑΣΚΗΣΗ 582 (Βαθμός δυσκολίας 6 , με κλίμακα από το 1 μέχρι το 10): Αν

και

είναι περιττός φυσικός αριθμός, και
αν ισχύει ότι :

, να βρεθούν οι αριθμοί

Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Τρί Νοέμ 03, 2015 4:59 pm
από kostas232
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 582 (Βαθμός δυσκολίας 6 , με κλίμακα από το 1 μέχρι το 10): Αν

και

είναι περιττός φυσικός αριθμός, και
αν ισχύει ότι :

, να βρεθούν οι αριθμοί

Από τη σχέση

προκύπτουν οι σχέσεις

και

Από τις (1) και (2) προκύπτει η σχέση

.
Παίρνοντας περιπτώσεις εύκολα βλέπουμε ότι η αρχική σχέση έχει τις λύσεις

με

πραγματικό αριθμό διάφορο του 0,1,-1.
Λαμβάνοντας υπ' όψιν το γεγονός ότι

,όπου

ακέραιος, λαμβάνουμε τις τριάδες

.
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Τρί Νοέμ 03, 2015 6:54 pm
από socrates
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 582 (Βαθμός δυσκολίας 6 , με κλίμακα από το 1 μέχρι το 10): Αν

και

είναι περιττός φυσικός αριθμός, και
αν ισχύει ότι :

, να βρεθούν οι αριθμοί

Δείτε και:
viewtopic.php?f=109&t=34737
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Τετ Νοέμ 04, 2015 12:53 am
από Μπάμπης Στεργίου
ΑΣΚΗΣΗ 583
Να αποδείξετε ότι ο αριθμός

είναι τέλειο τετράγωνο.
( Ρουμανία 2015)
Μπ
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Τετ Νοέμ 04, 2015 8:36 am
από Mihalis_Lambrou
Μπάμπης Στεργίου έγραψε:ΑΣΚΗΣΗ 583
Να αποδείξετε ότι ο αριθμός

είναι τέλειο τετράγωνο.
Γενικότερα




(τέλειο τετράγωνο).
Παράδειγμα

Φιλικά,
Μιχάλης
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Παρ Νοέμ 13, 2015 6:59 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
ΑΣΚΗΣΗ 584 (Βαθμός δυσκολίας 5, με κλίμακα από το 1 μέχρι το 10): Αν οι αριθμοί

είναι θετικοί ακέραιοι και

, και αν επί πλέον
οι αριθμοί

είναι ανάλογοι με τους αριθμούς

αντιστοίχως, να αποδείξετε ότι ο αριθμός

είναι τέλειο τετράγωνο
φυσικού αριθμού.
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Παρ Νοέμ 13, 2015 8:47 pm
από Mihalis_Lambrou
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 584 (Βαθμός δυσκολίας 5, με κλίμακα από το 1 μέχρι το 10): Αν οι αριθμοί

είναι θετικοί ακέραιοι και

, και αν επί πλέον
οι αριθμοί

είναι ανάλογοι με τους αριθμούς

αντιστοίχως,
να αποδείξετε ότι ο αριθμός  είναι τέλειο τετράγωνο φυσικού αριθμού.
είναι τέλειο τετράγωνο φυσικού αριθμού.
Ακόμα καλύτερα, βρείτε τα

(η απάντηση είναι μοναδική).
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Πέμ Νοέμ 26, 2015 7:09 pm
από kostas232
Άσκηση 585
Να βρείτε τον ελάχιστο θετικό ρητό αριθμό που μπορεί να γραφεί στη μορφή

, με

ακεραίους.
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Παρ Δεκ 11, 2015 8:44 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
kostas232 έγραψε:Άσκηση 585
Να βρείτε τον ελάχιστο θετικό ρητό αριθμό που μπορεί να γραφεί στη μορφή

, με

ακεραίους.
H δοσμένη παράσταση γράφεται:

. Για να γίνει η

ελάχιστη και θετική, πρέπει η παράσταση

να γίνει ελάχιστη
και θετική. Αφού οι
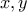
είναι ακέραιοι τότε η ελάχιστη θετική τιμή που μπορεί να πάρει η παράσταση

είναι το

. Αρκεί λοιπόν να δείξουμε ότι υπάρχουν

, ώστε

. Όμως βρίσκουμε ότι

. Άρα πράγματι υπάρχουν ακέραιοι
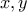
ώστε

, οπότε η ελάχιστη
θετική τιμή της

είναι η

. (Εύκολα βρίσκουμε ότι αυτό επιτυγχάνεται για

)
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Σάβ Δεκ 12, 2015 10:32 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
ΑΣΚΗΣΗ 586: Να αποδείξετε ότι η εξίσωση

, με

δεν έχει ρίζες ίσες.
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Κυρ Δεκ 13, 2015 2:33 pm
από kostas232
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:kostas232 έγραψε:Άσκηση 585
Να βρείτε τον ελάχιστο θετικό ρητό αριθμό που μπορεί να γραφεί στη μορφή

, με

ακεραίους.
H δοσμένη παράσταση γράφεται:

. Για να γίνει η

ελάχιστη και θετική, πρέπει η παράσταση

να γίνει ελάχιστη
και θετική. Αφού οι
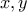
είναι ακέραιοι τότε η ελάχιστη θετική τιμή που μπορεί να πάρει η παράσταση

είναι το

. Αρκεί λοιπόν να δείξουμε ότι υπάρχουν

, ώστε

. Όμως βρίσκουμε ότι

. Άρα πράγματι υπάρχουν ακέραιοι
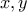
ώστε

, οπότε η ελάχιστη
θετική τιμή της

είναι η

. (Εύκολα βρίσκουμε ότι αυτό
επιτυγχάνεται για

)
Γενικά μπορούμε να πούμε ότι, επειδή

με

ακεραίους είναι

.
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Πέμ Δεκ 17, 2015 1:13 am
από socrates
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 586: Να αποδείξετε ότι η εξίσωση

, με

δεν έχει ρίζες ίσες.
Αν η δοθείσα εξίσωση έχει (ως προς

) δύο ίσες ρίζες, τότε

Επομένως,

Όμως,

Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Παρ Φεβ 05, 2016 7:37 am
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
ΑΣΚΗΣΗ 587:(Βαθμός δυσκολίας 4, με κλίμακα από 1 έως 10) Αν

, να λυθεί η εξίσωση:

Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Κυρ Φεβ 07, 2016 5:35 pm
από kostas232
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 587:(Βαθμός δυσκολίας 4, με κλίμακα από 1 έως 10) Αν

, να λυθεί η εξίσωση:

Η εξίσωση γράφεται

.
Αν

, τότε προφανώς κάθε ζεύγος

ικανοποιεί την εξίσωση (1).
Aν

τότε έχουμε

Για να έχει λύσεις η παραπάνω εξίσωση πρέπει
![\Delta \geq 0 \Leftrightarrow (y-1)^2 -4(y^2-y) \geq 0 \Leftrightarrow -3y^2+2y+1 \geq 0 \Leftrightarrow 3y^2-2y-1 \leq 0 \Leftrightarrow y\in \left [-\frac{2}{3}, 1 \right]} \Delta \geq 0 \Leftrightarrow (y-1)^2 -4(y^2-y) \geq 0 \Leftrightarrow -3y^2+2y+1 \geq 0 \Leftrightarrow 3y^2-2y-1 \leq 0 \Leftrightarrow y\in \left [-\frac{2}{3}, 1 \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/7877972d01ceb2ecbe2293b70c344d8f.png)
.
Όμως

, άρα

.
Για

έχουμε

.
Για

έχουμε

.
Συνολικά, λοιπόν, η (1) έχει στο

τις λύσεις

, όπου
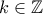
.
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Δημοσιεύτηκε: Κυρ Φεβ 07, 2016 6:27 pm
από Al.Koutsouridis
kostas232 έγραψε:ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 587:(Βαθμός δυσκολίας 4, με κλίμακα από 1 έως 10) Αν

, να λυθεί η εξίσωση:

Η εξίσωση γράφεται

.
Αν

, τότε προφανώς κάθε ζεύγος

ικανοποιεί την εξίσωση (1).
Aν

τότε έχουμε

Λίγο διαφορετικά απο εδώ και πέρα.




επειδή τα τετράγωνα είναι θετικά παρατηρούμε ότι θα πρέπει δυο από αυτά να είναι ίσα με ένα και το άλλο μηδέν που μας οδηγεί στις λύσεις

 , ο αριθμός
, ο αριθμός  δε διαιρείται με το
δε διαιρείται με το  .
. , ο αριθμός
, ο αριθμός  δε διαιρείται με το
δε διαιρείται με το  .
.ομάδες. Κάθε ομάδα έπαιξε με κάθε άλλη ακριβώς μία φορά. Σε κάθε αγώνα, η νικήτρια ομάδα κέρδιζε
βαθμούς, η ηττημένη
βαθμούς ενώ σε περίπτωση ισοπαλίας οι δύο ομάδες κέρδιζαν από
βαθμό. Στο τέλος του τουρνουά, διαπιστώθηκε ότι το άθροισμα των βαθμών που κέρδισαν όλες οι ομάδες ήταν
Να δείξετε ότι υπάρχουν τέσσερις ομάδες, καθεμία από τις οποίες έφερε μία, τουλάχιστον, φορά ισοπαλία.
 αγώνες.
αγώνες. οι αγώνες με νικητή και ηττημένο και
οι αγώνες με νικητή και ηττημένο και  οι αγώνες με ισοπαλία τότε
οι αγώνες με ισοπαλία τότε  και επειδή
και επειδή  ,
,  . Συνεπώς τέσσερις ομάδες καθεμία από τις οποίες έφερε μία, τουλάχιστον, φορά ισοπαλία.
. Συνεπώς τέσσερις ομάδες καθεμία από τις οποίες έφερε μία, τουλάχιστον, φορά ισοπαλία. , με
, με  , να αποδείξετε ότι:
, να αποδείξετε ότι:
 είναι θετικοί οι ρίζες, καθώς και τα κλάσματα, ορίζονται.
είναι θετικοί οι ρίζες, καθώς και τα κλάσματα, ορίζονται. , το δεύτερο με
, το δεύτερο με  και το τρίτο με
και το τρίτο με  , η ισότητα
, η ισότητα 
 και το τρίτο με
και το τρίτο με  οπότε η (1) γίνεται
οπότε η (1) γίνεται , που αληθεύει.
, που αληθεύει. δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του  Άρα και ο
Άρα και ο  δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του 
 όπου
όπου  ακέραιος. Τότε
ακέραιος. Τότε
 είναι πάντα πολλαπλάσιο του
είναι πάντα πολλαπλάσιο του  είναι πολλαπλάσιο του 3).
είναι πολλαπλάσιο του 3). είναι πολλαπλάσιο του 81 ενώ ο
είναι πολλαπλάσιο του 81 ενώ ο  διαιρούμενος με 81 αφήνει υπόλοιπο 27.
διαιρούμενος με 81 αφήνει υπόλοιπο 27. και
και  είναι περιττός φυσικός αριθμός, και
είναι περιττός φυσικός αριθμός, και  , να βρεθούν οι αριθμοί
, να βρεθούν οι αριθμοί 
 προκύπτουν οι σχέσεις
προκύπτουν οι σχέσεις  και
και 
 .
. με
με  ,όπου
,όπου  ακέραιος, λαμβάνουμε τις τριάδες
ακέραιος, λαμβάνουμε τις τριάδες .
.



 (τέλειο τετράγωνο).
(τέλειο τετράγωνο).
 είναι θετικοί ακέραιοι και
είναι θετικοί ακέραιοι και  , και αν επί πλέον
, και αν επί πλέον είναι ανάλογοι με τους αριθμούς
είναι ανάλογοι με τους αριθμούς  αντιστοίχως, να αποδείξετε ότι ο αριθμός
αντιστοίχως, να αποδείξετε ότι ο αριθμός  είναι τέλειο τετράγωνο
είναι τέλειο τετράγωνο , με
, με  ακεραίους.
ακεραίους. . Για να γίνει η
. Για να γίνει η  ελάχιστη και θετική, πρέπει η παράσταση
ελάχιστη και θετική, πρέπει η παράσταση  να γίνει ελάχιστη
να γίνει ελάχιστη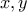 είναι ακέραιοι τότε η ελάχιστη θετική τιμή που μπορεί να πάρει η παράσταση
είναι ακέραιοι τότε η ελάχιστη θετική τιμή που μπορεί να πάρει η παράσταση  είναι το
είναι το  . Αρκεί λοιπόν να δείξουμε ότι υπάρχουν
. Αρκεί λοιπόν να δείξουμε ότι υπάρχουν , ώστε
, ώστε  . Όμως βρίσκουμε ότι
. Όμως βρίσκουμε ότι  . Άρα πράγματι υπάρχουν ακέραιοι
. Άρα πράγματι υπάρχουν ακέραιοι  , οπότε η ελάχιστη
, οπότε η ελάχιστη . (Εύκολα βρίσκουμε ότι αυτό επιτυγχάνεται για
. (Εύκολα βρίσκουμε ότι αυτό επιτυγχάνεται για  )
) , με
, με  δεν έχει ρίζες ίσες.
δεν έχει ρίζες ίσες. με
με  ακεραίους είναι
ακεραίους είναι  .
.


 , να λυθεί η εξίσωση:
, να λυθεί η εξίσωση: 
 .
. , τότε προφανώς κάθε ζεύγος
, τότε προφανώς κάθε ζεύγος  ικανοποιεί την εξίσωση (1).
ικανοποιεί την εξίσωση (1). τότε έχουμε
τότε έχουμε 
![\Delta \geq 0 \Leftrightarrow (y-1)^2 -4(y^2-y) \geq 0 \Leftrightarrow -3y^2+2y+1 \geq 0 \Leftrightarrow 3y^2-2y-1 \leq 0 \Leftrightarrow y\in \left [-\frac{2}{3}, 1 \right]} \Delta \geq 0 \Leftrightarrow (y-1)^2 -4(y^2-y) \geq 0 \Leftrightarrow -3y^2+2y+1 \geq 0 \Leftrightarrow 3y^2-2y-1 \leq 0 \Leftrightarrow y\in \left [-\frac{2}{3}, 1 \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/7877972d01ceb2ecbe2293b70c344d8f.png) .
. , άρα
, άρα  .
. έχουμε
έχουμε  .
. έχουμε
έχουμε  .
. τις λύσεις
τις λύσεις  , όπου
, όπου 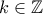 .
.



