
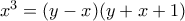

 ή
ή &
& 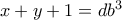
Εύκολα βρίσκουμε
 και μένει να λυθεί η εξίσωση
και μένει να λυθεί η εξίσωση  άρα
άρα  διαιρεί το
διαιρεί το  κ.τ.λ
κ.τ.λ Μοναδικές λύσεις

Συντονιστές: cretanman, Demetres, polysot, socrates, silouan

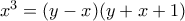

 ή
ή &
& 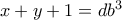
 και μένει να λυθεί η εξίσωση
και μένει να λυθεί η εξίσωση  άρα
άρα  διαιρεί το
διαιρεί το  κ.τ.λ
κ.τ.λ 
 θετικών ακέραιων αριθμών για τα οποία ισχύει:
θετικών ακέραιων αριθμών για τα οποία ισχύει: 
socrates έγραψε:8)
Να προσδιορίσετε όλα τα ζεύγηθετικών ακέραιων αριθμών για τα οποία ισχύει:
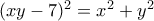
 θα καταλήξουμε στην
θα καταλήξουμε στην  ,
,  και η εξίσωση έχει λύσεις για
και η εξίσωση έχει λύσεις για  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  και βρίσκουμε απο την αρχική εξίσωση τις λύσεις που προκύπτουν πολύ εύκολα....
και βρίσκουμε απο την αρχική εξίσωση τις λύσεις που προκύπτουν πολύ εύκολα....
socrates έγραψε:9)


 έχουμε
έχουμε  ή
ή  Oι αριθμοί
Oι αριθμοί  ,
,  ,
,  είναι ανα 2 πρώτοι και δεδομένου ότι ο
είναι ανα 2 πρώτοι και δεδομένου ότι ο  δεν είναι ποτέ πολλαπλάσιο του
δεν είναι ποτέ πολλαπλάσιο του  θα πρέπει
θα πρέπει  ή
ή 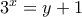 και βλέπουμε ότι δεν έχει άλλες λύσεις.
και βλέπουμε ότι δεν έχει άλλες λύσεις. .
.Δημήτρη, αυτό δεν είναι σωστό. Μάλλον θέλεις να πειςΑρχιμήδης 6 έγραψε:
Γιαέχουμε
ή
Oι αριθμοί
,
,
είναι ανα 2 πρώτοι και δεδομένου ότι ο
δεν είναι ποτέ πολλαπλάσιο του
θα πρέπει
ή
και βλέπουμε ότι δεν έχει άλλες λύσεις.
Μοναδικές λύσεις οι.
 ή
ή 
 είναι δύναμη πρώτου. Αν σκεφτείς πιο απλά ...η ποσότητα
είναι δύναμη πρώτου. Αν σκεφτείς πιο απλά ...η ποσότητα  είναι <<κρυμμένη>> στην ποσότητα
είναι <<κρυμμένη>> στην ποσότητα  και αφού ο
και αφού ο  δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του  τότε θα είναι κρυμμένη στην
τότε θα είναι κρυμμένη στην 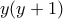 . Αν η ποσότητα διασπαστεί και καταμεριστεί στους
. Αν η ποσότητα διασπαστεί και καταμεριστεί στους  ,
,  τότε οι
τότε οι  ,
,  θα έχουν κοινό διαιρέτη τον
θα έχουν κοινό διαιρέτη τον  που είναι άτοπο. Άρα η δύναμη
που είναι άτοπο. Άρα η δύναμη  θα βρίσκεται ακριβώς σε έναν από τους
θα βρίσκεται ακριβώς σε έναν από τους  ή
ή  όπως είπα. Άρα
όπως είπα. Άρα  ή
ή  .Θανάση έχεις δίκιο! Το κατάλαβα λίγο αργά.
.Θανάση έχεις δίκιο! Το κατάλαβα λίγο αργά. . Bάζοντας λοιπόν όπου
. Bάζοντας λοιπόν όπου  βλέπουμε ότι το αριστερό μέλος είναι μεγαλύτερο απο το δεξί με λύσεις μόνο για
βλέπουμε ότι το αριστερό μέλος είναι μεγαλύτερο απο το δεξί με λύσεις μόνο για  άρα
άρα  .
. με τον ίδιο τρόπο έχει λύσεις για
με τον ίδιο τρόπο έχει λύσεις για  άρα
άρα  .
.
Λοιπόνsocrates έγραψε:Ωραία Δημήτρη!
10)

 και
και  ,
,  με
με  τελικά η εξίσωση θα γίνει...
τελικά η εξίσωση θα γίνει... Όμως
Όμως  και λύνουμε τις εξισώσεις ξεχωριστά ...
και λύνουμε τις εξισώσεις ξεχωριστά ... (1)
(1) 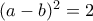 (2)
(2)  (3) Λόγο χρόνου την έγραψα σύντομα...Καλή συνέχεια.
(3) Λόγο χρόνου την έγραψα σύντομα...Καλή συνέχεια.



 Να δείξετε ότι ο αριθμός
Να δείξετε ότι ο αριθμός  είναι τέλειο τετράγωνο ακεραίου και
είναι τέλειο τετράγωνο ακεραίου και 
socrates έγραψε:
13)


 o
o  διαιρεί τον
διαιρεί τον  και τον
και τον  αλλά όχι και τον
αλλά όχι και τον  . Άρα
. Άρα  . Μοναδική λύση
. Μοναδική λύση  .
.Η εξίσωση γράφεταιsocrates έγραψε: 14)


 ισχύει
ισχύει  , άρα το
, άρα το  δε μπορεί να είναι τέλειο τετράγωνο για
δε μπορεί να είναι τέλειο τετράγωνο για  .
. έχουμε
έχουμε 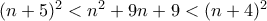 , άρα το
, άρα το  δε μπορεί να είναι τέλειο τετράγωνο για
δε μπορεί να είναι τέλειο τετράγωνο για 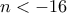 .
.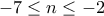 είναι
είναι  οπότε δε μπορεί να είναι τέλειο τετράγωνο ακεραίου.
οπότε δε μπορεί να είναι τέλειο τετράγωνο ακεραίου.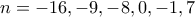 και με αντικατάσταση βρίσκουμε τις τιμές του
και με αντικατάσταση βρίσκουμε τις τιμές του  . Συγκεκριμένα έχουμε τις λύσεις
. Συγκεκριμένα έχουμε τις λύσεις 
socrates έγραψε:16)
Δίνεται η εξίσωσηΝα δείξετε ότι ο αριθμός
είναι τέλειο τετράγωνο ακεραίου και
Βρείτε μια λύση της εξίσωσης.

 ,
, 
 της μορφής ....
της μορφής ....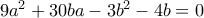
 και για να έχουμε ακέραιες λύσεις πρέπει να είναι τέλειο τετράγωνο άρα έστω ότι
και για να έχουμε ακέραιες λύσεις πρέπει να είναι τέλειο τετράγωνο άρα έστω ότι 
 ( Έστω
( Έστω  ) .
) .
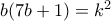 και αφού
και αφού  τότε υπάρχουν ακέραιοι
τότε υπάρχουν ακέραιοι  με
με  ώστε
ώστε  και
και  άρα
άρα 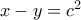 και προφανός το σύστημα έχει μικρότερη θετική λύση την
και προφανός το σύστημα έχει μικρότερη θετική λύση την  άρα
άρα  .
.Δε βρίσκω κάτι καλύτερο αυτή τη στιγμή από την παρακάτω λύση.socrates έγραψε: 15)

 , για κάθε
, για κάθε  .
.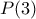 είναι αληθής.
είναι αληθής.  και ας υποθέσουμε ότι η
και ας υποθέσουμε ότι η  είναι αληθής δηλαδή
είναι αληθής δηλαδή  .
.
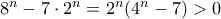 για
για 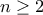 και αφετέρου είναι εύκολο να δείξουμε με επαγωγή ότι
και αφετέρου είναι εύκολο να δείξουμε με επαγωγή ότι  για
για 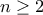 . Άρα η
. Άρα η  είναι αληθής και η επαγωγή ολοκληρώθηκε.
είναι αληθής και η επαγωγή ολοκληρώθηκε. . Πράγματι οι
. Πράγματι οι 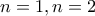 είναι λύσεις άρα και μοναδικές.
είναι λύσεις άρα και μοναδικές.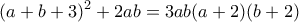
Μια λύση στην 11:socrates έγραψε:11)
 είναι
είναι 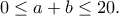
 οπότε
οπότε 
 .
. όπου
όπου  ακέραιοι και ισχύει ότι
ακέραιοι και ισχύει ότι 

 &
&  θα φτάσουμε στην παρακάτω εξίσωση :
θα φτάσουμε στην παρακάτω εξίσωση :
 θα πρέπει η διακρίνουσα
θα πρέπει η διακρίνουσα  να είναι τέλειο τετράγωνο ώστε να έχει ακέραιες λύσεις και έστω ότι αυτή είναι ίση με
να είναι τέλειο τετράγωνο ώστε να έχει ακέραιες λύσεις και έστω ότι αυτή είναι ίση με  .
. Άρα
Άρα 

 για δεδομένους
για δεδομένους  είναι πλέον πολύ εύκολη δεδομένου ότι το αριστερό μέλος της εξίσωσης
είναι πλέον πολύ εύκολη δεδομένου ότι το αριστερό μέλος της εξίσωσης  λόγω της
λόγω της  είναι θετικό .Είναι εμφανές ότι για να έχει λύσεις η αρχική εξίσωση λόγω της
είναι θετικό .Είναι εμφανές ότι για να έχει λύσεις η αρχική εξίσωση λόγω της  θα πρέπει
θα πρέπει  και πάντα η αρχική εξίσωση τελικά βλέπουμε ότι θα έχει πεπερασμένες λύσεις
και πάντα η αρχική εξίσωση τελικά βλέπουμε ότι θα έχει πεπερασμένες λύσεις  .
.
 να εξεταστεί αν η εξίσωση έχει άπειρες λύσεις στους ακεραίους .
να εξεταστεί αν η εξίσωση έχει άπειρες λύσεις στους ακεραίους .Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες