
23) Να αποδειχθεί ότι η εξίσωση
 έχει άπειρες λύσεις στους ακέραιους.
έχει άπειρες λύσεις στους ακέραιους.Συντονιστές: cretanman, Demetres, polysot, socrates, silouan

 έχει άπειρες λύσεις στους ακέραιους.
έχει άπειρες λύσεις στους ακέραιους.Αρχιμήδης 6 έγραψε:- 21 )

Για τους μη μηδενικούς και διαφορετικούς ανα 2 ακέραιουςνα εξεταστεί αν η εξίσωση έχει άπειρες λύσεις στους ακεραίους .
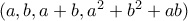
Είναι η 10.Γιώργος Απόκης έγραψε:22) Να λυθεί στους φυσικούς η εξίσωση
Γιώργος Απόκης έγραψε:23) Να αποδειχθεί ότι η εξίσωσηέχει άπειρες λύσεις στους ακέραιους.


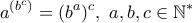
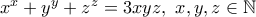
 ,
,  δεν ισχύει...
δεν ισχύει...Έχεις δίκιο Δημήτρη. Το διόρθωσα. Θενκς!Αρχιμήδης 6 έγραψε:Θανάση οι λύσεις που βρήκες για την εξίσωση μου είναι σωστές ? Νομίζω ότι πρέπει να διορθώσεις κάτι γιατί για,
δεν ισχύει...
Φιλικά ,
Δημήτρης
 ,
, 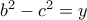 ,
,  τότε...
τότε...
socrates έγραψε:18)

 τότε
τότε 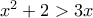


 .
.  .
.Μια προφανής λύση είναι ηsocrates έγραψε:26)

 ,έστω ο
,έστω ο  και οι άλλοι διάφοροι του
και οι άλλοι διάφοροι του  .
. έχουμε:
έχουμε:  απο ΑΜ-ΓΜ , άτοπο.
απο ΑΜ-ΓΜ , άτοπο.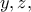 είναι μεγαλύτερος του
είναι μεγαλύτερος του  και ο άλλος μικρότερος του
και ο άλλος μικρότερος του  εύκολα βλέπουμε ότι η δοθείσα δεν έχει λύση.
εύκολα βλέπουμε ότι η δοθείσα δεν έχει λύση. είναι ίσοι με
είναι ίσοι με  πάλι εύκολα βλέπουμε ότι πάλι η εξίσωση δεν έχει λύσεις (εκτός από την 3,3,3)
πάλι εύκολα βλέπουμε ότι πάλι η εξίσωση δεν έχει λύσεις (εκτός από την 3,3,3)
 έχουμε
έχουμε  αδύνατο.
αδύνατο. ,ας πούμε ο
,ας πούμε ο  ,καί οι άλλοι δύο μεγαλύτεροι του θα είναι:
,καί οι άλλοι δύο μεγαλύτεροι του θα είναι: πάλι άτοπο.
πάλι άτοπο. ,έστω ο
,έστω ο  τότε διακρίνοντας τις περιπτώσεις
τότε διακρίνοντας τις περιπτώσεις  ή
ή  ή
ή 
 ευκολα βρίσκουμε τις λύσεις
ευκολα βρίσκουμε τις λύσεις  και
και 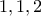
 και τα κυκλικά
και τα κυκλικάsocrates έγραψε: 25)

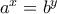 ΄τότε υπάρχουν φυσικοί
΄τότε υπάρχουν φυσικοί  ώστε
ώστε  ,
, 
 στην αρχική εξίσωση θα καταλήξουμε στην ισότητα...
στην αρχική εξίσωση θα καταλήξουμε στην ισότητα...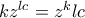 και διακρίνοντας περιπτώσεις θα έχουμε...
και διακρίνοντας περιπτώσεις θα έχουμε... ΄τότε
΄τότε 
 τότε
τότε 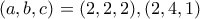
 τότε
τότε 
socrates έγραψε: 24)

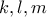 .
.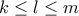 . Προφανώς θα ισχύει ότι
. Προφανώς θα ισχύει ότι  .
. ,
, 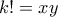 ,
,  ,
, 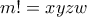 .
. ΄και κάνοντας τις πράξεις θα καταλήξουμε στην παρακάτω εξίσωση !
΄και κάνοντας τις πράξεις θα καταλήξουμε στην παρακάτω εξίσωση !
 πρέπει πέρνουμε σαν λύσεις
πρέπει πέρνουμε σαν λύσεις 


Γιώργος Απόκης έγραψε:23) Να αποδειχθεί ότι η εξίσωσηέχει άπειρες λύσεις στους ακέραιους.


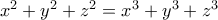

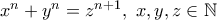



Οι λύσεις της εξίσωσηςsocrates έγραψε:31)
 είναι άπειρες και ισχύει μόνο για οποιουσδήποτε διαδοχικούς ακέραιους
είναι άπειρες και ισχύει μόνο για οποιουσδήποτε διαδοχικούς ακέραιους  . Πράγματι ισχύει και η ταυτότητα ...
. Πράγματι ισχύει και η ταυτότητα ... που είναι πολύ όμορφη ταυτότητα.
που είναι πολύ όμορφη ταυτότητα. παραλείπεται λόγω πληρότητας των απαιτήσεων της ανωτέρω άσκησης.
παραλείπεται λόγω πληρότητας των απαιτήσεων της ανωτέρω άσκησης. εννοείς για κάθε
εννοείς για κάθε  ?
?Ναι, τοΑρχιμήδης 6 έγραψε:Για την Άσκηση.
Οι λύσεις της εξίσωσηςείναι άπειρες και ισχύει μόνο για οποιουσδήποτε διαδοχικούς ακέραιους
. Πράγματι ισχύει και η ταυτότητα ...
που είναι πολύ όμορφη ταυτότητα.
Edit: H απόδειξη της μοναδικότητας της παραπάνω απειρίας τριάδωνπαραλείπεται λόγω πληρότητας των απαιτήσεων της ανωτέρω άσκησης.
Ερώτηση προς Θανάση: Στις ασκήσειςεννοείς για κάθε
?
 είναι ένας δεδομένος φυσικός αριθμός!
είναι ένας δεδομένος φυσικός αριθμός!socrates έγραψε: 27)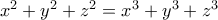
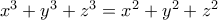

28) Aνsocrates έγραψε:Οι επόμενες εξισώσεις έχουν άπειρες ακέραιες ρίζες:
28)
29)
30)
 τότε η εξίσωση γίνεται
τότε η εξίσωση γίνεται  η οποία έχει άπειρες ακέραιες λύσεις
η οποία έχει άπειρες ακέραιες λύσεις 
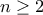 τότε
τότε  από όπου προκύπτει ότι
από όπου προκύπτει ότι  για κάθε
για κάθε 
 προκύπτει ότι
προκύπτει ότι  για κάθε
για κάθε 
 ώστε
ώστε  τότε
τότε  για κάθε
για κάθε 

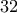 .
.

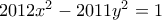
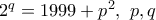 πρώτοι
πρώτοι

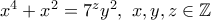

Οκ, για τους ακέραιους... Αν θέλουμε φυσικούς τότε μια οικογένεια είναιΑρχιμήδης 6 έγραψε:
Το βρήκα....
Θα ήθελα να δω όμως και κάτι πιο χρήσιμο απο την δική μου διαπύστωση...

Μέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 5 επισκέπτες