Μια ακόμα λύση, μετά τη λύση του Ορέστη, με λίγη καθυστέρησηsocrates έγραψε: 12)
Η εξίσωση είναι ισοδύναμη με τις ακόλουθες:



 Αν
Αν  και
και  ή το ανάποδο τότε
ή το ανάποδο τότε  που είναι αδύνατη.
που είναι αδύνατη. Αν
Αν  και
και  τότε
τότε 
 Αν
Αν  και
και  τότε
τότε 
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
Μια ακόμα λύση, μετά τη λύση του Ορέστη, με λίγη καθυστέρησηsocrates έγραψε: 12)



 Αν
Αν  και
και  ή το ανάποδο τότε
ή το ανάποδο τότε  που είναι αδύνατη.
που είναι αδύνατη. Αν
Αν  και
και  τότε
τότε 
 Αν
Αν  και
και  τότε
τότε 
Αν
 τότε
τότε  , που δεν έχει λύσεις στους θετικούς ακεραίους (αν
, που δεν έχει λύσεις στους θετικούς ακεραίους (αν  , τότε
, τότε  , άτοπο, άρα
, άτοπο, άρα  που δεν ικανοποιεί)
που δεν ικανοποιεί) τότε
τότε  . Αν
. Αν  , τότε
, τότε  , άτοπο. Άρα
, άτοπο. Άρα  , απ'όπου προκύπτει η λύση
, απ'όπου προκύπτει η λύση  .
. .
. . Προφανώς,
. Προφανώς,  οπότε έχουμε δύο περιπτώσεις:
οπότε έχουμε δύο περιπτώσεις: , οπότε
, οπότε  που δίνει
που δίνει  και άρα
και άρα  , άτοπο για
, άτοπο για  .
. οπότε
οπότε  .
. . Εύκολα βλέπουμε ότι όλοι τους είναι ίσοι με
. Εύκολα βλέπουμε ότι όλοι τους είναι ίσοι με  ή
ή  .
. διαιρεί δύο διαφορετικούς παράγοντες του
διαιρεί δύο διαφορετικούς παράγοντες του  , θα διαιρεί και τον Μ.Κ.Δ. αυτών, δηλαδή
, θα διαιρεί και τον Μ.Κ.Δ. αυτών, δηλαδή  ή
ή  , οπότε
, οπότε  άτοπο (
άτοπο ( ).
). ή
ή  ή
ή  ή
ή  .
. , οπότε
, οπότε  και εύκολα ελέγχουμε ότι η ανισότητα
και εύκολα ελέγχουμε ότι η ανισότητα  ισχύει μόνο για
ισχύει μόνο για 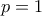 , άτοπο.
, άτοπο. , πρέπει
, πρέπει  με
με  θετικό ακέραιο, και με αντικατάσταση προκύπτει
θετικό ακέραιο, και με αντικατάσταση προκύπτει  .
. , είναι
, είναι  συνεπώς
συνεπώς  που ισχύει μόνο για
που ισχύει μόνο για  , άρα
, άρα  , άτοπο.
, άτοπο. , πρέπει
, πρέπει  με
με  θετικό ακέραιο, οπότε
θετικό ακέραιο, οπότε  .
. που ισχύει μόνο για
που ισχύει μόνο για  , άτοπο.
, άτοπο. , οπότε μοναδική λύση η
, οπότε μοναδική λύση η  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες