ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Δευ Φεβ 05, 2024 10:47 am
ΑΣΚΗΣΗ 1287 Σε κάποιες εκλογές για την ανάδειξη μιας τριμελούς επιτροπής, υπήρχαν τέσσερις υποψήφιοι , οι Α,Β,Γ,Δ.
Κάθε ψηφοφόρος μπορούσε να ψηφίσει το πολύ τρεις υποψήφιους. Μετά την καταμέτρηση των ψήφων, έλαβαν:
Ο Α

, ο Β

, ο Γ

και ο Δ
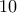
ψήφους, ενώ δεν υπήρχαν άκυρα ούτε λευκά.
(α) Να βρείτε πόσοι τουλάχιστον ήταν οι ψηφοφόροι.
(β) Αν οι ψηφοφόροι ήταν όσους βρήκατε στο (α) ερώτημα, και αν δεν υπήρξε ψηφοφόρος που να ψήφισε την τριάδα (Β,Γ,Δ), να βρείτε
πόσοι τουλάχιστον και πόσοι το πολύ από αυτούς ψήφισαν την τριάδα (Α,Β,Γ);
Γράφω μια λύση:
(α) Όλοι οι σταυροί ήταν συνολικά 68
Για να βρούμε τον ελάχιστο αριθμό των ψηφοφόρων, πρέπει να υποθέσουμε ότι όσο το δυνατόν περισσότεροι ψήφισαν και τους τρεις υποψήφιους.
Επειδή τώρα
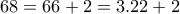
, αυτό σημαίνει ότι για να βρούμε τον ελάχιστο αριθμό που ζητάμε, θα θεωρήσουμε ότι

άτομα
ψήφισαν και τους τρεις από τους τέσσερις υποψήφιους, ενώ ένα μόνο άτομο ψήφισε τους δύο από τους τέσσερις.
Άρα ο ελάχιστος αριθμός των ψηφοφόρων ήταν
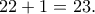
(β)Έχουμε σαν δεδομένο, ότι οι ψηφοφόροι ήταν

.
Θα διακρίνουμε τις εξής περιπτώσεις:
(1).

άτομα ψήφισαν την τριάδα (Α,Β,Γ) ,

άτομα την (Α,Β,Δ) ,

άτομα την (Α,Γ,Δ) ενώ ο ένας το ζεύγος (Γ,Δ)
Τότε έχουμε το σύστημα:
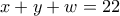
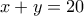
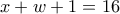
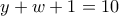
Από τις τρεις πρώτες εξισώσεις, άμεσα βρίσκουμε ότι
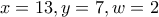
, και ότι με τις τιμές αυτές επαληθεύεται και η τέταρτη εξίσωση.
Άρα σε αυτή την περίπτωση, την τριάδα (Α,Β,Γ) την ψήφισαν

άτομα.
(2).

άτομα ψήφισαν την τριάδα (Α,Β,Γ) ,

την (Α,Β,Δ) ,

την (Α,Γ,Δ) ενώ ο ένας το ζεύγος (Β,Δ)
Τότε έχουμε έχουμε το σύστημα:
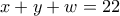
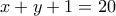
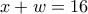
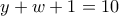
Και άμεσα βρίσκουμε ότι έχει την λύση

Άρα σε αυτή την περίπτωση, την τριάδα (Α,Β,Γ) την ψήφισαν επίσης

άτομα.
(3).

άτομα ψήφισαν την τριάδα (Α,Β,Γ) ,

την (Α,Β,Δ) ,

την (Α,Γ,Δ) ενώ ο ένας το ζεύγος (Β,Γ)
Τότε ομοίως βρίσκουμε ότι το σύστημα που θα προκύψει έχει την λύση
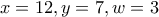
Άρα σε αυτήν την περίπτωση , την τριάδα (Α,Β,Γ) την ψήφισαν
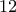
άτομα.
(4)

άτομα ψήφισαν την τριάδα (Α,Β,Γ) ,

την (Α,Β,Δ) ,

την (Α,Γ,Δ) ενώ ο ένας το ζεύγος (Α,Β)
Τότε έχουμε το σύστημα:

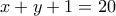
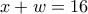
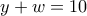
Λύνοντας το σύστημα των τριών πρώτων εξισώσεων άμεσα βρίσκουμε
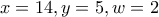
Αντικαθιστώντας όμως τις τιμές αυτές στην τέταρτη εξίσωση, παίρνουμε
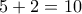
και άρα η περίπτωση αυτή απορρίπτεται
Όμοια απορρίπτονται και οι περιπτώσεις όπου το ένα άτομο ψήφησε τα ζεύγη (Α,Γ) ή (Α,Δ)
Άρα η τριάδα (Α,Β,Γ) έλαβε τουλάχιστον
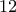
και το πολύ

ψήφους
 είναι γνωστό άθροισμα. Εργαζόμαστε λοιπόν για
είναι γνωστό άθροισμα. Εργαζόμαστε λοιπόν για  .
.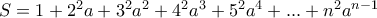 , άρα
, άρα 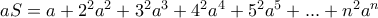 . Αφαιρούμε
. Αφαιρούμε 
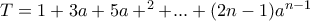 . Εδώ
. Εδώ 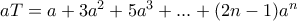 . Αφαιρούμε
. Αφαιρούμε  .
.  στην παράσταση του
στην παράσταση του  στην
στην  .
.


 είναι διαδοχικοί φυσικοί αριθμοί (
είναι διαδοχικοί φυσικοί αριθμοί (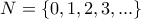 ) και ο
) και ο  είναι επίσης φυσικός αριθμός, να βρεθούν όλες οι δυνατές λύσεις της εξίσωσης
είναι επίσης φυσικός αριθμός, να βρεθούν όλες οι δυνατές λύσεις της εξίσωσης 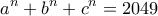
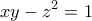
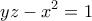
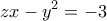

 . Άρα
. Άρα 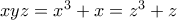 . Επειδή η συνάρτηση
. Επειδή η συνάρτηση 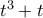 είναι γνήσια αύξουσα (άμεσο) έπεται ότι
είναι γνήσια αύξουσα (άμεσο) έπεται ότι  (το ίδιο συμπέρασμα βγαίνει και αλλιώς, θεωρώντας την
(το ίδιο συμπέρασμα βγαίνει και αλλιώς, θεωρώντας την 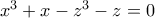 και παραγοποιώντας).
και παραγοποιώντας). 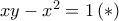 , ισοδύναμα
, ισοδύναμα  , και η τρίτη
, και η τρίτη  , ισοδύναμα
, ισοδύναμα  . Διαιρώντας κατά μέλη τις
. Διαιρώντας κατά μέλη τις 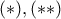 έχουμε μετά την απλοποίηση του (μη μηδενικού) όρου
έχουμε μετά την απλοποίηση του (μη μηδενικού) όρου  , ότι
, ότι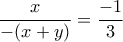 , οπότε
, οπότε 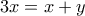 , δηλαδή
, δηλαδή  . H
. H  , άρα
, άρα  . Εύκολα τώρα βρίσκουμε ότι
. Εύκολα τώρα βρίσκουμε ότι 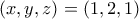 ή
ή 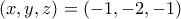 , που με έλεγχο επαληθεύουν τις αρχικές.
, που με έλεγχο επαληθεύουν τις αρχικές.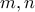 , ώστε ο αριθμός:
, ώστε ο αριθμός: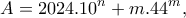 να είναι τέλειο τετράγωνο ακεραίου.
να είναι τέλειο τετράγωνο ακεραίου. είναι ακέραιοι και αν :
είναι ακέραιοι και αν :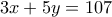 και
και 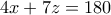
 με το
με το 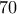
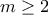 , έχουμε:
, έχουμε: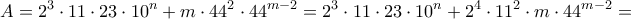
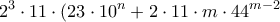
 τέλειο τετράγωνο, πρέπει:
τέλειο τετράγωνο, πρέπει: 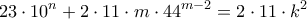 ,
, 
 να είναι πολλαπλάσιο του
να είναι πολλαπλάσιο του  , άτοπο, αφού ούτε ο
, άτοπο, αφού ούτε ο  , ούτε ο
, ούτε ο 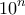 είναι πολλαπλάσια του
είναι πολλαπλάσια του  , ή
, ή 
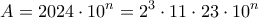 , που δεν είναι τέλειο τετράγωνο, αφού ο
, που δεν είναι τέλειο τετράγωνο, αφού ο 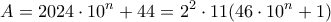
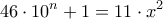 , όπου
, όπου 
 , άρα
, άρα  , ενώ
, ενώ 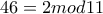
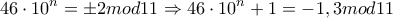 ,
,  .
. και
και 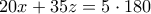

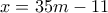 , όπου
, όπου 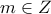 .
.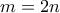 . Τότε:
. Τότε: 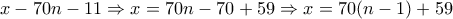

 . Τότε
. Τότε 

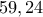
 , ο Β
, ο Β  , ο Γ
, ο Γ  και ο Δ
και ο Δ 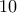 ψήφους, ενώ δεν υπήρχαν άκυρα ούτε λευκά.
ψήφους, ενώ δεν υπήρχαν άκυρα ούτε λευκά.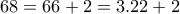 , αυτό σημαίνει ότι για να βρούμε τον ελάχιστο αριθμό που ζητάμε, θα θεωρήσουμε ότι
, αυτό σημαίνει ότι για να βρούμε τον ελάχιστο αριθμό που ζητάμε, θα θεωρήσουμε ότι 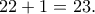
 άτομα την (Α,Β,Δ) ,
άτομα την (Α,Β,Δ) ,  άτομα την (Α,Γ,Δ) ενώ ο ένας το ζεύγος (Γ,Δ)
άτομα την (Α,Γ,Δ) ενώ ο ένας το ζεύγος (Γ,Δ)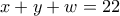
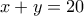
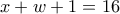
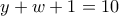
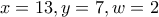 , και ότι με τις τιμές αυτές επαληθεύεται και η τέταρτη εξίσωση.
, και ότι με τις τιμές αυτές επαληθεύεται και η τέταρτη εξίσωση. άτομα.
άτομα.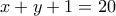
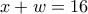

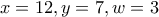
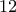 άτομα.
άτομα.
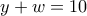
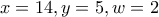
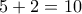 και άρα η περίπτωση αυτή απορρίπτεται
και άρα η περίπτωση αυτή απορρίπτεται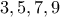
 αντιστοίχως.
αντιστοίχως. , (1)
, (1)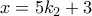 , (2)
, (2)  , (3)
, (3)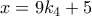 , (4)
, (4) ,
, 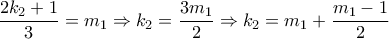 , (5)
, (5)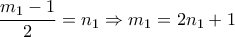 .
. και στη συνέχεια η (2) γράφεται:
και στη συνέχεια η (2) γράφεται: 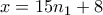 , (6).
, (6). αφήνει υπόλοιπο
αφήνει υπόλοιπο  και διαιρούμενος με το
και διαιρούμενος με το  αφήνει υπόλοιπο
αφήνει υπόλοιπο 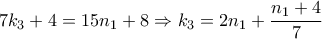 ,
, 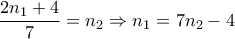
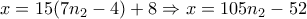 , (7)
, (7) , αφήνει υπόλοιπο
, αφήνει υπόλοιπο  αντιστοίχως).
αντιστοίχως).

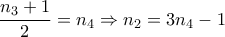 .
.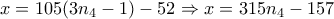 .
.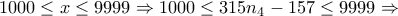
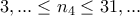

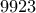 . Το
. Το  ο ζητούμενος, παρατηρεί κανείς ότι ο
ο ζητούμενος, παρατηρεί κανείς ότι ο  είναι πολλαπλάσιο των
είναι πολλαπλάσιο των 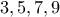 . Πράγματι η συνθήκη
. Πράγματι η συνθήκη 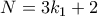 δίνει
δίνει 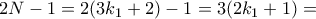 πολλαπλάσιο του
πολλαπλάσιο του  .
.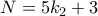 δίνει
δίνει 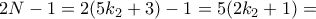 πολλαπλάσιο του
πολλαπλάσιο του  .
. 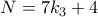 και
και 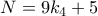 .
. . Θέλουμε ο
. Θέλουμε ο 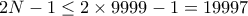 . To μεγαλύτερο πολλαπλάσιο του
. To μεγαλύτερο πολλαπλάσιο του  που είναι
που είναι 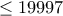 είναι το
είναι το 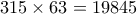 . Άρα
. Άρα 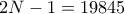 , οπότε
, οπότε 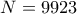 .
.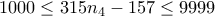 συμπέρανα ότι
συμπέρανα ότι 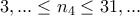 ενώ το σωστό είναι:
ενώ το σωστό είναι:  . Οπότε η μέγιστη τιμή του
. Οπότε η μέγιστη τιμή του  και άρα αυτή θα είναι:
και άρα αυτή θα είναι: 
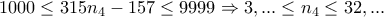

 %
% και λιγότεροι από
και λιγότεροι από 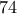
 . Άρα
. Άρα 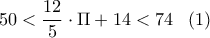 .
.  προκύπτει
προκύπτει  , μετά
, μετά 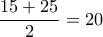 .
. 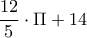 πρέπει να είναι ακέραιος, αφού εκφράζει το πλήθος των εκδρομέων.
πρέπει να είναι ακέραιος, αφού εκφράζει το πλήθος των εκδρομέων.  , όπου
, όπου  είναι φυσικός αριθμός. Έτσι, ο αριθμός των εκδρομέων είναι
είναι φυσικός αριθμός. Έτσι, ο αριθμός των εκδρομέων είναι 
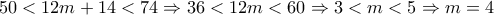
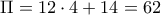
 .
.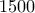 επιβάτες, ξεκίνησε από την πόλη Α
επιβάτες, ξεκίνησε από την πόλη Α  των επιβατών,
των επιβατών, 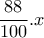 των επιβατών και αφού ανέβηκαν ακόμα
των επιβατών και αφού ανέβηκαν ακόμα 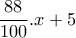 επιβάτες.
επιβάτες.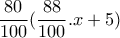 επιβάτες και αφού ανέβηκαν και
επιβάτες και αφού ανέβηκαν και  επιβάτες, δηλαδή με
επιβάτες, δηλαδή με 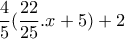
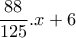 επιβάτες. Ο αριθμός όμως αυτός πρέπει να είναι φυσικός. Άρα πρέπει ο
επιβάτες. Ο αριθμός όμως αυτός πρέπει να είναι φυσικός. Άρα πρέπει ο  , δηλαδή
, δηλαδή 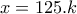 , με
, με  φυσικό αριθμό.
φυσικό αριθμό.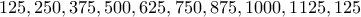 και
και  και
και 
 διαιρείται με το
διαιρείται με το 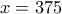
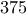 επιβάτες και στην πόλη Β έφτασαν
επιβάτες και στην πόλη Β έφτασαν  , δηλαδή
, δηλαδή  επιβάτες.
επιβάτες.