Είναι:



Με πρόσθεση κατά μέλη και αφού κάνουμε τα αναπτύγματα παίρνουμε:

Και άρα:

Και συνεπώς:

ή
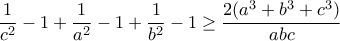 ,
,ή

Συντονιστές: cretanman, Demetres, polysot, socrates, silouan






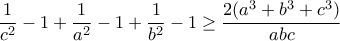 ,
,
 , για τις διάφορες τιμές του φυσικού αριθμού
, για τις διάφορες τιμές του φυσικού αριθμού  .
.ΕίναιΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Μάιος 29, 2019 6:38 pmΑΣΚΗΣΗ 1376 Να βρεθεί το ψηφίο των μονάδων του αριθμού:
, για τις διάφορες τιμές του φυσικού αριθμού
.

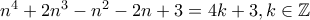

 λήγει πάντα σε
λήγει πάντα σε  .
. , λήγει σε
, λήγει σε  , αν ο
, αν ο  είναι περιττός και σε
είναι περιττός και σε  , αν
, αν  είναι θετικός άρτιος. Στη συνέχεια να βρείτε τα δύο τελευταία ψηφία του αριθμού
είναι θετικός άρτιος. Στη συνέχεια να βρείτε τα δύο τελευταία ψηφία του αριθμού 
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Σάβ Φεβ 06, 2021 11:36 pmΑΣΚΗΣΗ 1377 Να αποδείξετε ότι ο αριθμός, λήγει σε
, αν ο
είναι περιττός και σε
, αν
οείναι θετικός άρτιος. Στη συνέχεια να βρείτε τα δύο τελευταία ψηφία του αριθμού

 και
και  και έχω:
και έχω: :
: 

 και
και  ισοδύναμα
ισοδύναμα 
 αν γνωρίζουμε ότι ο αριθμός
αν γνωρίζουμε ότι ο αριθμός 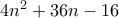 διαιρείται με το
διαιρείται με το 
Απλά για ένα γειά στον Άριστο Μαθηματικό, Δάσκαλο και πολύ φίλο Δημήτρη.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Κυρ Φεβ 28, 2021 10:42 pmΑΣΚΗΣΗ 1378 Να βρεθεί ο θετικός ακέραιοςαν γνωρίζουμε ότι ο αριθμός
διαιρείται με το

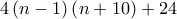 να διαιρείται από τον
να διαιρείται από τον  αρκεί ο
αρκεί ο  να διαιρείται από τον
να διαιρείται από τον  άρα
άρα 
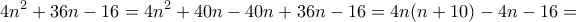
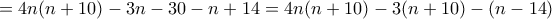
 να διαιρεί τον
να διαιρεί τον  . Άρα θα πρέπει ή ο
. Άρα θα πρέπει ή ο  ή
ή 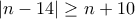
 ή
ή  , (που απορρίπτεται) ή
, (που απορρίπτεται) ή 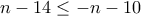
 ή
ή  . Άρα
. Άρα  ή
ή  (που απορρίπτεται) ή
(που απορρίπτεται) ή 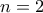 (που είναι δεκτό).
(που είναι δεκτό). , έχει τουλάχιστον
, έχει τουλάχιστον  και το πολύ
και το πολύ  ψηφία.
ψηφία.Δημήτρη, σου κάνει αυτό:ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Απρ 20, 2022 9:28 pmΑΣΚΗΣΗ 1279: Να αποδείξετε ότι ο αριθμός, έχει τουλάχιστον
και το πολύ
ψηφία.
(ΣΗΜΕΙΩΣΗ: Η άσκηση προέκυψε ύστερα από μια συζήτηση με τον συνάδελφο Βασίλη Μάρκο. Υπάρχει ανοικτό το θέμα, το αν μπορούμε να βρούμε ακριβώς το πόσα είναι τα ψηφία του εν λόγω αριθμού, με γνώσεις μόνο σχολικές ή έστω και με μη σχολικές)
 , ισχύει με πολύ ασφάλεια
, ισχύει με πολύ ασφάλεια  .
.  , οπότε
, οπότε  .
. έχει
έχει 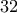 ψηφία.
ψηφία.Καλό Πάσχα Μιχάλη. Ναι, είναι ένας ωραίος τρόπος να βρούμε το πόσα ψηφία έχει ο αριθμός μας.Mihalis_Lambrou έγραψε: ↑Πέμ Απρ 21, 2022 1:20 amΔημήτρη, σου κάνει αυτό:ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Απρ 20, 2022 9:28 pmΑΣΚΗΣΗ 1279: Να αποδείξετε ότι ο αριθμός, έχει τουλάχιστον
και το πολύ
ψηφία.
(ΣΗΜΕΙΩΣΗ: Η άσκηση προέκυψε ύστερα από μια συζήτηση με τον συνάδελφο Βασίλη Μάρκο. Υπάρχει ανοικτό το θέμα, το αν μπορούμε να βρούμε ακριβώς το πόσα είναι τα ψηφία του εν λόγω αριθμού, με γνώσεις μόνο σχολικές ή έστω και με μη σχολικές)
Αφού από πίνακες λογαρίθμων της εποχής που ήμουν μαθητής έχουμε, ισχύει με πολύ ασφάλεια
.
Άρα, οπότε
.
Η διπλή αυτή ανισότητα δείχνει ότι οέχει
ψηφία.
.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Πέμ Απρ 21, 2022 8:02 pm
ΑΣΚΗΣΗ 1279: Να αποδείξετε ότι ο αριθμός, έχει τουλάχιστον
και το πολύ
ψηφία.
.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Απρ 20, 2022 9:28 pmΤο να δείξουμε ότι έχει ή 31 ή 32 ψηφία, βγαίνει με σχολική ύλη Γυμνασίου.
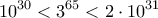 (τα οποία άκρα έχουν
(τα οποία άκρα έχουν  και
και 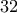 ψηφία, αντίστοιχα).
ψηφία, αντίστοιχα). και
και 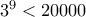 (στην πραγματικότητα είναι
(στην πραγματικότητα είναι  ). Έτσι
). Έτσι και
και .
. .
. , έχουμε:
, έχουμε: 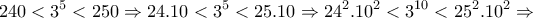


 και
και 
 .
. .
.  έχει
έχει  ψηφία και ο αριθμός
ψηφία και ο αριθμός  έχει
έχει  ψηφία.
ψηφία.  έχει τουλάχιστον
έχει τουλάχιστον  και το πολύ
και το πολύ  ψηφία.
ψηφία.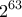 σπυριά σιτάρι, μπορούμε να βρούμε το πλήθος των
σπυριά σιτάρι, μπορούμε να βρούμε το πλήθος των  , (αν εργαστούμε κατάλληλα με παρόμοιο όπως πριν τρόπο).
, (αν εργαστούμε κατάλληλα με παρόμοιο όπως πριν τρόπο). (προφανώς).
(προφανώς).  σπυριά σιτάρι (που ήδη ο αριθμός αυτός είναι υπερβολικός), τότε τα
σπυριά σιτάρι (που ήδη ο αριθμός αυτός είναι υπερβολικός), τότε τα 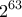
 κιλά, δηλαδή περισσότερο από
κιλά, δηλαδή περισσότερο από 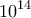 κιλά, δηλαδή περισσότερο
κιλά, δηλαδή περισσότερο τόνους. Και επειδή μια μεγάλη νταλίκα χωράει
τόνους. Και επειδή μια μεγάλη νταλίκα χωράει 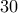 τόνους σιτάρι, θα χρειαστούμε περισσότερες από
τόνους σιτάρι, θα χρειαστούμε περισσότερες από  :
: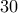
 δισεκατομμύρια νταλίκες!!!!
δισεκατομμύρια νταλίκες!!!!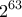 , είναι βέβαιο, ότι και αν κάθε κάτοικος του πλανήτη είχε από μία νταλίκα,
, είναι βέβαιο, ότι και αν κάθε κάτοικος του πλανήτη είχε από μία νταλίκα, .ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Πέμ Απρ 21, 2022 8:02 pmΑΣΚΗΣΗ 1279: Να αποδείξετε ότι ο αριθμός, έχει τουλάχιστον
και το πολύ
ψηφία.
.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Απρ 20, 2022 9:28 pm... Το πόσα ακριβώς όμως έχει, μάλλον μόνο με χρήση λογαρίθμων πρέπει να βρίσκεται.
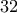 ψηφία. Ο παρακάτω τρόπος είναι μακρόσυρτος αλλά δεν θα περίμενε κανείς θεαματική βελτίωση διότι ο
ψηφία. Ο παρακάτω τρόπος είναι μακρόσυρτος αλλά δεν θα περίμενε κανείς θεαματική βελτίωση διότι ο  είναι πολύ κοντά στον
είναι πολύ κοντά στον 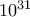 (βλέπε τελευταία γραμμή του προηγούμενου ποστ) οπότε οι διαδοχικές εκτιμήσεις που κάνουμε πρέπει να είναι αρκετά "σφιχτές".
(βλέπε τελευταία γραμμή του προηγούμενου ποστ) οπότε οι διαδοχικές εκτιμήσεις που κάνουμε πρέπει να είναι αρκετά "σφιχτές". 


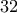 ψηφία, αλλά ήδη είδαμε ότι έχει το πολύ
ψηφία, αλλά ήδη είδαμε ότι έχει το πολύ 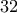 , συνεπώς ακριβώς
, συνεπώς ακριβώς 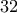 .
. υπάρχουν, που είναι μεγαλύτεροι από το
υπάρχουν, που είναι μεγαλύτεροι από το  και
και , ώστε ο αριθμός
, ώστε ο αριθμός 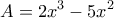 να είναι τέλειο τετράγωνο.
να είναι τέλειο τετράγωνο. είναι τέλειο τετράγωνο, άρα και ο αριθμός
είναι τέλειο τετράγωνο, άρα και ο αριθμός 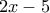 είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο.  . Οπότε επειδή ο
. Οπότε επειδή ο  είναι περιττός, έχουμε
είναι περιττός, έχουμε  λύσεις.
λύσεις. και αφού ο
και αφού ο  είναι τετράγωνος, θα πρέπει και ο
είναι τετράγωνος, θα πρέπει και ο  να είναι επίσης τετράγωνος. Άρα πρέπει
να είναι επίσης τετράγωνος. Άρα πρέπει , όπου
, όπου  ακέραιος και χωρίς βλάβη της γενικότητας, μπορούμε να υποθέσουμε ότι ο
ακέραιος και χωρίς βλάβη της γενικότητας, μπορούμε να υποθέσουμε ότι ο  είναι θετικός
είναι θετικός είναι περιττός, ως διαφορά ενός περιττού από έναν άρτιο. Άρα και ο
είναι περιττός, ως διαφορά ενός περιττού από έναν άρτιο. Άρα και ο  θα είναι επίσης περιττός .
θα είναι επίσης περιττός . , όπου ο
, όπου ο  είναι μη αρνητικός ακέραιος.
είναι μη αρνητικός ακέραιος. και άρα
και άρα 
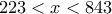 . Άρα πρέπει
. Άρα πρέπει  και άρα
και άρα 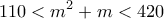 ,
,  και
και  .
. είναι μη αρνητικός ακέραιος, βρίσκουμε
είναι μη αρνητικός ακέραιος, βρίσκουμε
 είναι
είναι 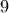
 άσπρες κότες παίρνουμε καθημερινά
άσπρες κότες παίρνουμε καθημερινά  αβγά ενώ από
αβγά ενώ από  κόκκινες κότες παίρνουμε
κόκκινες κότες παίρνουμε αβγά.
αβγά.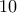 ευρώ την μία και κάποιες κόκκινες προς
ευρώ την μία και κάποιες κόκκινες προς 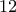 ευρώ την μία και πληρώσαμε
ευρώ την μία και πληρώσαμε  ευρώ, ενώ παίρνουμε καθημερινά
ευρώ, ενώ παίρνουμε καθημερινά  αβγά.
αβγά. άσπρες κότες παίρνουμε καθημερινά
άσπρες κότες παίρνουμε καθημερινά  αυγά. Από
αυγά. Από  κόκκινες κότες παίρνουμε καθημερινά
κόκκινες κότες παίρνουμε καθημερινά  αυγά. Συνεπώς οι άσπρες κότες είναι πιο παραγωγικές.
αυγά. Συνεπώς οι άσπρες κότες είναι πιο παραγωγικές. άσπρες και
άσπρες και  κόκκινες κότες. Έχουμε:
κόκκινες κότες. Έχουμε:

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες