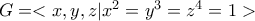 ,
, 
ΔΕΝ είναι ισόμορφες.
Δεν έχω σίγουρα σωστή απάντηση...
Συντονιστής: Demetres
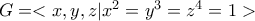 ,
, 
 η συμμετρική ομάδα των μεταθέσεων του συνόλου
η συμμετρική ομάδα των μεταθέσεων του συνόλου  .
.  ως εξής: Ορίζω
ως εξής: Ορίζω  και
και  και επεκτείνω. (Αυτό επιτρέπεται γιατί υπάρχει μοναδική επέκταση της
και επεκτείνω. (Αυτό επιτρέπεται γιατί υπάρχει μοναδική επέκταση της  σε ομομορφισμό
σε ομομορφισμό  και εύκολα ελέγχεται ότι σε αυτήν την επέκταση
και εύκολα ελέγχεται ότι σε αυτήν την επέκταση  , και άρα παίρνω ένα καλώς ορισμένο ομομορφισμό
, και άρα παίρνω ένα καλώς ορισμένο ομομορφισμό  .) Παρατηρώ επίσης ότι ο ομομορφισμός
.) Παρατηρώ επίσης ότι ο ομομορφισμός  είναι επί.
είναι επί. . Πράγματι αν υπήρχε, τότε θα έπρεπε τα
. Πράγματι αν υπήρχε, τότε θα έπρεπε τα  να μην είναι ταυτοτικά, αλλιώς ο ομομορφισμός δεν θα ήταν επί. Αλλά τότε το
να μην είναι ταυτοτικά, αλλιώς ο ομομορφισμός δεν θα ήταν επί. Αλλά τότε το  είναι στοιχείο τάξης 6 στο
είναι στοιχείο τάξης 6 στο  . Όμως τέτοια στοιχεία δεν υπάρχουν στο
. Όμως τέτοια στοιχεία δεν υπάρχουν στο  , άτοπο.
, άτοπο.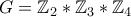 ενώ η δεύτερη είναι η
ενώ η δεύτερη είναι η 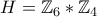 .
.Από που προκύπτουν αυτά ;giannispapav έγραψε: ↑Δευ Ιούλ 19, 2021 8:30 amΜια κάπως διαφορετική προσέγγιση:
Η πρώτη ομάδα είναι προφανώς ηενώ η δεύτερη είναι η
.
Οι ομάδες αυτές δεν μπορεί να είναι ισόμορφες (για παράδειγμα από τη μοναδικότητα της Grushko διάσπασης)
Νομίζω ότι η εκφώνηση είναι ελλιπής.
 πάνω στο σύνολο
πάνω στο σύνολο  και έστω
και έστω  ένα υποσύνολο της
ένα υποσύνολο της  (το σύνολο
(το σύνολο  παίζει το ρόλο των σχέσεων), τότε ορίζουμε την παράσταση
παίζει το ρόλο των σχέσεων), τότε ορίζουμε την παράσταση  να είναι η ομάδα
να είναι η ομάδα 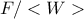 , δηλαδή το πηλίκο της
, δηλαδή το πηλίκο της  με την ελάχιστη κανονική υποομάδα της
με την ελάχιστη κανονική υποομάδα της  που περιέχει το
που περιέχει το  . Οπότε καταλήγουμε πως οι παραστάσεις ομάδων ορίζουν ομάδες ως προς ισομορφισμό.
. Οπότε καταλήγουμε πως οι παραστάσεις ομάδων ορίζουν ομάδες ως προς ισομορφισμό.ΑνΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Ιούλ 19, 2021 2:40 pmΑπό που προκύπτουν αυτά ;giannispapav έγραψε: ↑Δευ Ιούλ 19, 2021 8:30 amΜια κάπως διαφορετική προσέγγιση:
Η πρώτη ομάδα είναι προφανώς ηενώ η δεύτερη είναι η
.
Οι ομάδες αυτές δεν μπορεί να είναι ισόμορφες (για παράδειγμα από τη μοναδικότητα της Grushko διάσπασης)
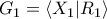 και
και  τότε χρησιμοποιώντας την καθολική συνθήκη των ελευθέρων γινομένων μπορεί να αποδειχθεί ότι
τότε χρησιμοποιώντας την καθολική συνθήκη των ελευθέρων γινομένων μπορεί να αποδειχθεί ότι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες