Πραγματικός δακτύλιος (;)
Δημοσιεύτηκε: Σάβ Οκτ 05, 2024 10:26 am
Καλημέρα σε όλους μετά από πολύ καιρό. Θα ήθελα μία βοήθεια από τους αγγλομαθείς αλγεβριστές της ομάδας. Πρόσφατα, στο μάθημα της Αλγεβρικής Γεωμετρίας που παρακολουθώ, ήρθα σε επαφή με την έννοια του "anello reale" ("πραγματικός δακτύλιος") ως ενός δακτυλίου  (αντιμεταθετικού με μονάδα) που ικανοποιεί την ιδιότητα
(αντιμεταθετικού με μονάδα) που ικανοποιεί την ιδιότητα
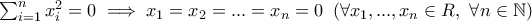
Μετά από μία (ομολογουμένως όχι επισταμένη) έρευνα στο internet, βρήκα παρεμφερείς έννοιες αλλά πουθενά αυτόν τον συγκεκριμένο ορισμό. Ξέρει κανείς την αγγλική/ελληνική απόδοση;
Ευχαριστώ πολύ!
 (αντιμεταθετικού με μονάδα) που ικανοποιεί την ιδιότητα
(αντιμεταθετικού με μονάδα) που ικανοποιεί την ιδιότητα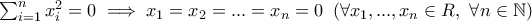
Μετά από μία (ομολογουμένως όχι επισταμένη) έρευνα στο internet, βρήκα παρεμφερείς έννοιες αλλά πουθενά αυτόν τον συγκεκριμένο ορισμό. Ξέρει κανείς την αγγλική/ελληνική απόδοση;
Ευχαριστώ πολύ!
 , μαζί με τη συνηθισμένη με τα αλγεβρικά κλειστά σώματα (που δεν επιδέχονται γνήσια αλγεβρική επέκταση), όπως το
, μαζί με τη συνηθισμένη με τα αλγεβρικά κλειστά σώματα (που δεν επιδέχονται γνήσια αλγεβρική επέκταση), όπως το  .
.